Матан / Экстремумы функции нескольких переменных

Экстремум функции нескольких переменных.

Необходимый признак существования экстремума дифференцируемой функции.

Пусть функция имеет экстремум в точке и дифференцируема в этой точке.

Тогда все частные производные в точке .

Информация:

Главными минорами матрицы 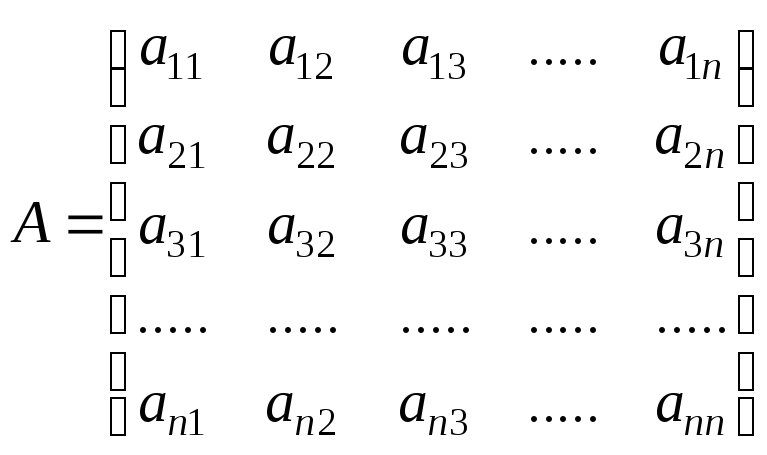называются определители левого верхнего угла:

, , , . . . . ,

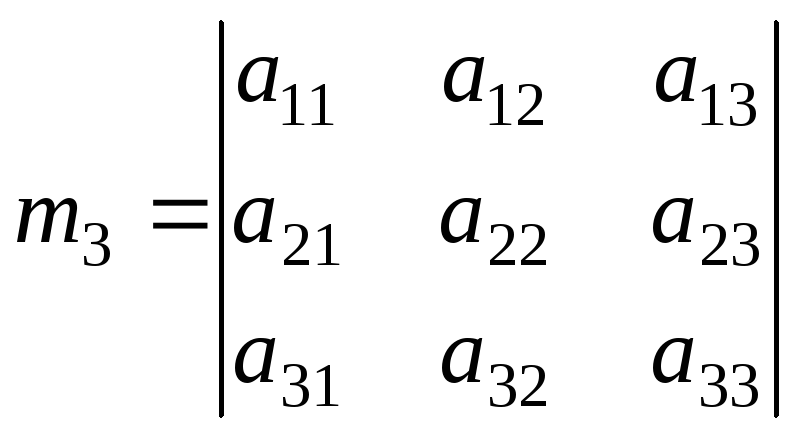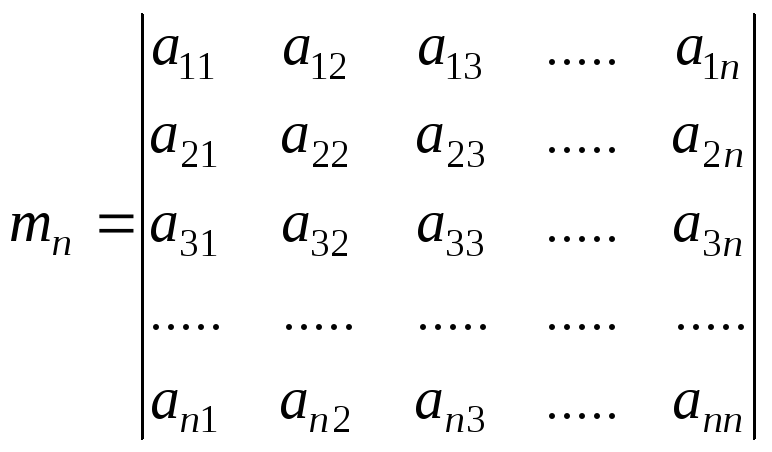
Стационарными точками функции называются точки, в которых выполнено необходимое условие существования экстремума (т.е. точки, «подозрительные» на экстремум).

Достаточный признак существования экстремума дифференцируемой функции.

Рассматривается функция . Пусть

– в точке все частные производные функции и

– в точке главные миноры матрицы

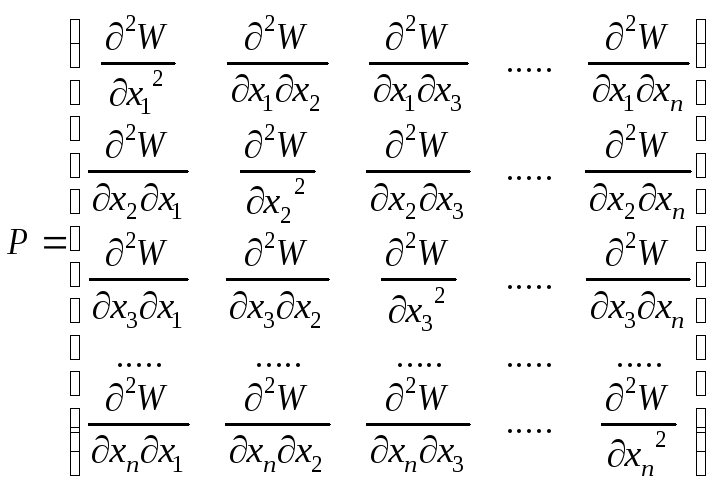
имеют знаки или

Тогда в первом случае в точке функция имеет , во втором случае – .

При любых других распределениях знаков главных миноров функция не имеет экстремума в точке .

Случай равенства нулю каких-то главных миноров требует отдельного рассмотрения.