2.Векторная алгебра
2.1Векторы в пространстве R3
Линейное векторное пространство R3 образует множество матриц размерности 3х1 с обычными для матриц операциями сложения и умножения на скаляр. Каждый элемент a этого пространства (вектор) имеет вид:
r |
x |
|
|
|
|
a . |
|
a |
= y , где x, y, z - координаты вектора |
||
|
|
|
|
|
z |
|
|
Скалярное произведение в R3 определяется, как и в разделе “Элементы линейной алгебры”:
|
r |
|
|
x |
|
(ar |
+ y1 y2 |
+ z1 z2 , если ar |
1 |
r |
|
,b )= x1 x2 |
= y1 |
, b |
|||
|
|
|
|
|
|
|
|
|
|
z1 |
|
x2
=y2 .z2
|
|
|
|
|
|
|
r |
x |
|
r |
|
|
|
|
|
|
|
|
|
|
= x2 + y2 + z2 . |
||
Норма или модуль вектора a |
= y |
вычисляется по формуле: |
a |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
Для скалярного произведения справедливы следующие законы: |
|
|
|||||||||
1) |
(ar,br)= (br,ar), |
,cr), |
ar, b R3 . |
|
|
||||||
2) |
(ar+br,cr)=(ar |
,cr)+(br |
ar, b, cr R3 . |
|
|
||||||
|
r |
r |
r |
ar, b R3 , α - число. |
|
|
|||||
3) |
(α ar,b )= (ar,αb )=α |
(ar,b ), |
|
|
|||||||
4) |
(ar,ar)= |
|
ar |
|
2 , |
|
|
ar R 3 . |
|
|
|
|
|
|
|
|
|
||||||
Базис в R3 определяется, как и в разделе “Элементы линейной алгебры”. Базис векторов i , j , k будем считать стандартным. В дальнейшем, если это специально не оговорено, под координатами вектора будем понимать координаты в этом базисе, т.е.
r |
|
x |
|
r |
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a |
= y |
= xi |
+ yj |
+ zk . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1. |
Вычислить скалярное произведение векторов |
||||||||||||||||||
|
|
|
2 |
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
− 3 |
r |
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
a |
= |
, b |
= |
|
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
− 2,4 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
r |
|
|
|
2 |
|
1,5 |
8,5 |
|
r |
2 |
|||||
|
|
|
|
= |
2 |
|
− |
|
+3 |
|
−1 |
|
|
−9 |
|
|
|||
Решение. c1 |
|
3 |
|
|
= |
|
; c2 |
= −4 − |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
−2,4 |
|
|
−5,2 |
|
|
|
(cr |
,cr |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|||||
)=8,5 (−6,5)+(−9) 11+(−5,2) (−6,4)= −120,97. |
|||||||||||||||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cr1 = 2ar+3b и cr2 = −4ar+br , если
|
1,5 |
|
−6,5 |
|
||
|
|
−1 |
|
|
|
|
3 |
+ |
|
= 11 |
. |
||
|
|
−2,4 |
|
|
−6,4 |
|
|
|
|
|
|
||
Ответ. –120,97.
6
Определение. |
|
|
|
|
|
|
Векторы ar |
и b будем называть ортогональными, |
если их скалярное произведение |
||||
r |
|
|
|
|
|
|
(ar,b )= 0 . |
|
|
|
|
|
|
|
r |
3 |
|
m |
|
|
|
|
r |
|
4 |
|
|
Пример 2. При каком значении m векторы a |
= −2 |
и b |
= |
ортогональны? |
||
|
|
|
|
|
0,5 |
|
|
|
1 |
|
|
|
|
Решение.
(ar,br)=3 m +(−2) 4 +1 0,5 =3m −7,5. Из условия ортогональности векторов следует:
3m −7,5 = 0 , или m = 2,5 .
Ответ. 2,5.
2.2 Геометрическое изображение вектора в R3 . Линейные операции с
векторами. Геометрический смысл скалярного произведения
В пространстве R3 векторная |
алгебра |
допускает наглядную геометрическую |
||||
интерпретацию. В этом пространстве вектор a |
изображается множеством направленных |
|||||
отрезков, имеющих длину, равную |
|
ar |
|
|
и одинаковое направление. Иначе говоря, вектор в R3 |
|
|
|
|||||
изображается направленным отрезком, начало которого может располагаться в любой точке трехмерного Евклидова пространства.
Линейные операции над векторами
1) Сложение
ar+br
ar
b
x |
|
x |
|
|
x |
+ x |
|
|
|
|
1 |
|
|
2 |
|
1 |
|
2 |
|
= y1 |
|
+ y2 |
|
= y1 + y2 |
. |
||||
z |
1 |
|
z |
2 |
|
z |
+ z |
2 |
|
|
|
|
|
1 |
|
|
|||
a |
b |
ar +b 
ar +b
Рис. 2.1.
2) Вычитание
|
r |
x |
|
x |
|
|
x |
− x |
|
|
||
ar |
|
1 |
|
|
2 |
|
|
1 |
|
2 |
|
|
−b |
= y1 |
|
− y2 |
|
= y1 − y2 |
. |
||||||
|
|
z |
1 |
|
z |
2 |
|
z |
1 |
− z |
2 |
|
|
|
|
|
|
|
|
|
|
||||
a
ar −b
b
Рис. 2.2.
7
3) Умножение на число
α r =α x1 a y1
z1
a
α = αα
x1 y1 . z1
α a (α > 0)
α a (α < 0)
Рис. 2.3.
|
|
|
|
|
|
3 |
|
|
0,6 |
|
||
Пример 1. Найти |
|
r |
r |
|
r |
|
− 2 |
|
r |
|
0,8 |
|
|
|
|||||||||||
|
2a |
+3b |
|
, если a |
= |
|
и b |
= |
. |
|||
|
|
|
|
|
|
|
0,5 |
|
|
|
4,1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
r |
3 |
|
|
0,6 |
|
|
2 |
3 +3 0,6 |
7,8 |
|
||||
2ar |
|
− 2 |
|
+3 |
|
0,8 |
|
|
|
2 |
(− 2)+3 0,8 |
|
|
|
|
+3b |
= 2 |
|
|
|
= |
|
= −1,6 |
, |
|||||||
|
|
|
0,5 |
|
|
|
4,1 |
|
|
|
2 |
0,5 +3 4,1 |
|
|
|
|
r |
|
|
|
|
|
|
|
|
13,3 |
|
||||
r |
= 7,82 |
+1,6 |
2 +13,32 |
= |
240,29 . |
|
|
|
|||||||
2a |
+3b |
|
|
|
|||||||||||
Ответ. |
240,29 . |
|
|
|
|
|
|
|
|
|
|
|
|||
Геометрический смысл скалярного произведения
a |
ar −b |
|
α |
b
Рис. 2.4.
По свойству скалярного произведения:
ar −br 2 = (ar −br,ar −br)= (ar,ar)−(ar,br)−(br,ar)+ (br,br)= ar 2 −2(ar,br)+ br 2 .
С другой стороны, по теореме косинусов: |
|
r |
r |
|
2 |
= |
|
r |
|
2 |
− 2 |
|
r |
|
|
|
r |
|
cosα + |
|
r |
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
a |
−b |
|
|
|
a |
|
|
|
a |
|
|
|
b |
|
|
b |
|
. |
|||||||||||||||||||||
Следовательно (ar,br)= |
|
ar |
|
|
|
br |
|
cosα , где |
|
α – |
|
угол между векторами a и b . |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Пример 2. Найти (cr |
,cr |
), если cr = 5 ar +b ; cr |
= 4 ar −b ; |
|
|
|
ar |
|
= 2 , |
|
br |
|
= 3 , ar b =120o . |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||
1 |
2 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение.
(cr1 , cr2 )= (5 ar + br, 4 ar − br)=5 4 (ar, ar)+ 4 (b, ar)−5 (ar, b )− (b, b )=
8
= 20 ar 2 − (ar, br)− br 2 == 20 ar 2 − ar br cos(ar br)− br 2 =80 − 2 3 cos120o − 9 = =80 − 6 (− 0,5)− 9 = 74.
Ответ. 74 .
Следует заметить, что для скалярного произведения векторов выполняются те же законы, что и для алгебраических операций с многочленами. Из этого следует, что при
скалярном умножении векторов справедливы формулы сокращенного умножения. |
||||||||||||
Пример 3. Вычислить |
|
cr |
|
, если c = 5 p − 2 q ; |
|
ps |
|
= 3 , |
|
qr |
|
= 4 , pr qr = 60o . |
|
|
|
|
|
|
|||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
||
|
cr |
|
2 = (cr,cr)= (5 pr − 2 qr,5 pr − 2 qr)= (5 pr − 2 qr)2 = 25 pr2 − 2 10 (pr,qr)+ 4 qr2 = |
1 |
|
||||||||||||||||
|
|
|
|||||||||||||||||||
= 25 |
|
pr |
|
2 − 20 |
|
pr |
|
|
|
qr |
|
cos(pr qr)+ 4 |
|
qr |
|
2 = 25 9 − 20 3 4 cos 60o + 4 16 = 225 − 240 |
+ |
||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 |
|||||||||||||||
+ 64 =169. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ. 13.
Из геометрического смысла скалярного произведения следует, что ортогональные векторы должны изображаться перпендикулярными направленными отрезками.
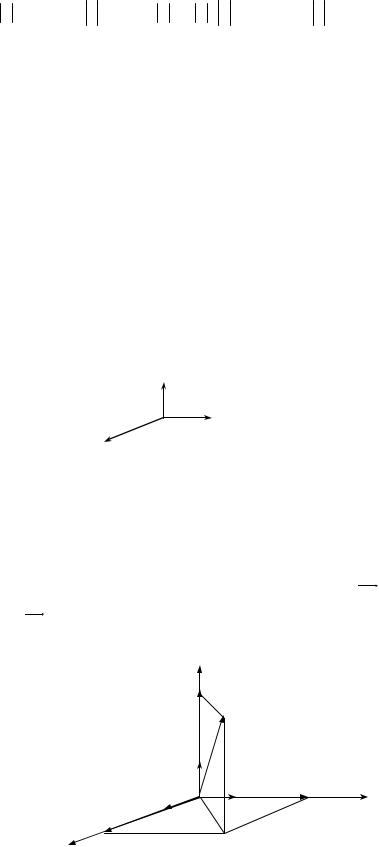
Рассмотрим стандартный ортонормированный базис i , j , k и изобразим эти векторы единичными (длина которых равна 1), взаимно перпендикулярными отрезками с общим началом в некоторой точке O .
|
k |
|
ir |
О |
j |
Векторы ir, j , k |
Рис. 2.5. |
|
будем располагать так, чтобы с конца k вращение от i к j |
||
происходило против часовой стрелки (рис. 2.5). Такой базис называется базисом правой ориентации.
Введем прямоугольную декартову систему координат с началом в точке O , ось Ox |
||||||
сонаправим с вектором ir |
, ось Оу – с вектором |
j , а ось Oz – с вектором k . Тогда вектор |
||||
r |
r |
r |
|
|
|
OA . При этом x, y, z – это |
ar = x i |
+ y j |
+ z k изобразится направленным отрезком |
||||
проекции OA на координатные оси или координаты точки A |
в системе координат xyz (рис. |
|||||
2.6). |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
zk |
А |
ar = x i + y j + z k |
|
|
|
|
k |
j |
yj |
у |
|
|
xir |
i |
о |
|
|
|
|
|
|
|
|
|
|
х |
|
xi + yj |
|
|
|
Рис. 2.6.
9