
модуль 2.14
.pdf
ФИЗИКА
Модуль 2.14
ГЛАВА 9 Уравнение Максвелла
1 Вихревое электрическое поле
Пусть индукционный ток в замкнутом контуре обусловлен изменениями магнитного поля. Это указывает на то, что изменения магнитного поля вызывают появление в контуре сторонних сил. Эти силы не связаны ни с химическими, ни с тепловыми процессами в проводнике, они также не могут быть магнитными силами, так как такие силы работы над
зарядами не совершают. Остается заключить, что индукционный ток обусловлен
возникающим в проводнике электрическим полем. Пусть EВ - напряженность этого поля. Электродвижущая сила равна циркуляции вектора напряженности сторонних сил (в
|
|
|
|
|
|
|
|
данном случае это |
EВ ) по контуру: |
|
|||||
i |
|
|
|
|
|
|
|
EB dl . |
|
|
|
(9.1) |
|||
|
|
|
|
||||
Согласно формуле (8.1) ЭДС, индуцированная в контуре, равна: |
|
||||||
i |
d |
|
d |
|
|
|
|
dt |
dt |
BdS , |
(9.2) |
||||
|
|
|
S |
|
|
||
|
|
|
|
|
|
|
|
где S |
- произвольная поверхность, ограниченная контуром. |
|
|||||
Приравняв правые части формул (9.1) и (9.2), придем к соотношению: |
|
||||||
|
|
|
d |
|
|
|
|
|
EB dl |
|
dt |
BdS |
|||||
|
|
|
S |
|
|
|||
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
||||||
EB dl |
|
t |
dS |
|
||||
|
|
|
S |
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
(9.3)
Вектор |
|
B |
зависит, вообще говоря, как от времени, так и от координат, поэтому под |
||||||
знаком интеграла написали символ частной производной по времени. |
|||||||||
Преобразуем левую часть равенства (9.3) по теореме Стокса (1.64). В результате |
|||||||||
получим, что |
|
|
|
|
|
||||
|
|
|
|
|
|
B |
|
||
rotE |
B |
dS |
|
t |
dS . |
|
|||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
S |
|
|
Отсюда |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
B . |
|
(9.4) |
||||
rotE |
B |
|
|||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, ротор поля EB в каждой точке пространства равен взятой |
|||||||||
|
|
|
|
|
|
|
|
|
|
с обратным знаком производной по времени от вектора B . |
|||||||||
Дж. |
К. |
Максвелл предположил, что изменяющееся со временем магнитное поле |
|||||||
|
|
|
|
|
|
|
|
|
|
обуславливает появление в пространстве поле |
EB независимо от присутствия в этом |
||||||||
|
|
|
|
|
|
|
|
|
|
пространстве проводящего контура. Поле EB существенно отличается от порождаемого |
|||||||||
|
|
|
|
|
|
|
|
|
|
неподвижными |
зарядами электростатического |
поля E q . Электростатическое поле |
|||||||
потенциально, его линии напряженности начинаются и оканчиваются на зарядах.
1

Ротор вектора |
|
в любой точке равен нулю: |
E q |
rotE |
q |
0 |
|
|
|
|
|
|
|||
Согласно (9.4) ротор вектора |
отличен от нуля. Следовательно, поле |
||||
EB |
|||||
E
(9.5)
B |
, как и |
магнитное поле, является вихревым.
Итак, электрическое поле может быть как потенциальным (
|
|
E |
q |
|
), так и вихревым
(
|
|
E |
B |
|
). В общем случае
|
|
|
E |
E |
q |
|
|
|
|
E |
B |
|
,
где поле
|
|
E |
q |
|
создается зарядами, а поле
|
|
E |
B |
|
обусловлено изменяющимся со временем магнитным полем. Сложив соотношения (9.4) и
(9.5), получим |
|
|
|
|
|
B |
|
|
rotE |
t |
(9.6) |
|
||
|
|
Это уравнение является одним из основных в электромагнитной теории Максвелла.
2 Ток смещения
Теория электромагнитного поля, начала которой заложил Фарадей, математически была завершена Максвеллом. При этом одной из важнейших новых идей, выдвинутых Максвеллом, была мысль о симметрии в зависимости электрического и магнитного полей.
А именно, поскольку меняющееся во времени магнитное поле
|
B |
||
|
t |
|
|
|
|
||
|
|||
создает
электрическое поле, следует ожидать, что меняющееся во времени электрическое поле
|
|
|
|
|
E |
||
|
|
|
|
|
t |
|
|
|
|
||
|
|||
создает магнитное поле.
К этой идее можно придти путем, например, следующих рассуждений.
Рассмотрим процессы, происходящие при прохождении переменного тока по цепи, содержащей конденсатор (рис. 1).
Рис. 1
2

Ранее было показано, что линии тока, возникающие при разряде конденсатора, незамкнутые. Стационарному, то есть постоянному, току всегда соответствуют замкнутые линии тока.
В диэлектрике между пластинами конденсатора заряды не могут перемещаться, в результате чего линии тока, подходящие к пластине конденсатора, обрываются у ее поверхности. Ток проводимости, текущей по проводнику, соединяющему обкладки конденсатора, оказывается разомкнутым.
Однако согласно закону неразрывности силовые линии тока непрерывны. Рассмотрим, когда это условие выполняется.
При разряде конденсатора течет ток проводимости внутри обкладок, плотность которого по величине равна
jпров |
|
1 dq |
|
d |
, |
|||
S |
dt |
dt |
||||||
|
|
|
|
|||||
где |
q |
- поверхностная плотность заряда. |
||||||
S |
||||||||
|
|
|
|
|
|
|
||
Что же происходит в пространстве между пластинами конденсатора?
По теореме Гаусса согласно формулам (1.23) и (4.13) электрическое смещение зазоре конденсатора равно поверхностной плотности заряда на обкладке:
D
в
D 0 E . |
|
|
|||||
Отсюда |
|
|
|
|
|||
D |
|
|
|
|
|
|
|
t |
t |
|
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
||
Вектор |
D |
направлен |
от B пластины к |
A |
|||
t |
|||||||
|
|
|
|
|
|
||
конденсатора |
поле между |
пластинами убывает, |
|||||
|
|
|
|
|
|
|
|
направлен в сторону противоположную D . |
|
||||||
Левая часть уравнения (9.7) дает плотность так
(9.7)
(см. рис. 1), так как при разряде
|
|
|
|
|
|
поэтому |
D |
0 |
, т.е. вектор |
D |
|
t |
t |
||||
|
|
|
называемого тока смещения в зазоре
|
|
|
|
|
D |
||
j |
см ещ |
t |
|
|
|
||
|
|
|
|
Правая часть уравнения (9.7) – плотность тока проводимости
|
|
j |
пров |
|
|
(9.8)
. Равенство этих
плотностей означает, что на границе обкладок линии тока проводимости непрерывно переходят в линии тока смещения, т.о.
|
|
|
j |
пров |
|
|
S |
|
|
|
|
|
|
|
j |
см ещ |
S |
|
||
|
|
|
.
Другими словами, конденсатор в цепи переменного тока не прерывает ток, так как на пластинах конденсатора меняются заряды, а вместе с ними меняется и электрическое поле в конденсаторе.
Вывод: если существует переменное электрическое поле, то в контуре протекает электрический ток, условно названный током смещения.
Согласно гипотезе, высказанной Максвеллом, ток смещения создает в пространстве, его окружающем, магнитное поле такое же, как и магнитное поле эквивалентного тока проводимости. Эта гипотеза в настоящее время подтверждена многочисленными опытными фактами.
Следует иметь в виду, что ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле. Во всех других отношениях ток смещения не может быть подобен току проводимости, например, при прохождении тока
3

смещения не выделяется джоулево тепло, ток смещения не зарядом.
Сумму тока проводимости и тока смещения принято
Плотность полного тока равна: |
||||||
|
|
|
|
|||
j |
полн |
j |
пров |
j |
смещ |
|
|
|
|
|
|||
связан с перемещением
называть полным током.
(9.9)
Впроводнике jсмещ jпров .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, теорему о циркуляции вектора |
H , которая была установлена для постоянных |
||||||||||||
токов, можно обобщить для произвольного случая и записать: |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Hdl |
|
j |
пр |
dS |
j |
|
|
dS |
|
|||
|
|
|
|
|
|
см ещ |
|
|
|||||
или учитывая (9.8), |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
D |
|
||||||
|
Hdl |
|
|
|
|
jdS |
|
|
|
||||
|
|
|
|
dS |
(9.10) |
||||||||
|
|
|
|
|
|
|
t |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
где j |
jпр |
|
- ток проводимости. |
|
|||||||||
Дифференциальная форма уравнения (9.10): |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
D |
|
|
|
|
|
|||||
rotH |
|
j |
|
t |
|
, |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
т.е.
D
t
или
|
|
|
|
H |
j |
||
ротор вектора |
|
||
H |
|||
в той же точке.
|
|
D |
|
t |
, |
|
определяется плотностью тока проводимости
j
(9.11)
и тока смещения
3 Система уравнений Максвелла
С введением тока смещения макроскопическая теория электромагнитного поля была блестяще завершена. Основным следствием теории Максвелла был вывод о существовании электромагнитных волн, распространяющихся со скоростью света.
Основу теории образуют четыре уравнения Максвелла. Мы уже познакомились с каждым из них в отдельности, а сейчас просто соберем их все вместе.
В интегральной форме система уравнений Максвелла имеет следующий вид: |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|||||
Edl |
t |
dS , |
|
|
(9.12) |
||||||||
|
|
|
|
|
|||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|||
BdS |
|
, |
|
|
|
|
|
(9.13) |
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||||
Hdl |
|
|
|
D |
, |
|
(9.14) |
||||||
j |
t |
dS |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
DdS |
dV , |
|
|
|
(9.15) |
||||||||
где - объемная плотность сторонних зарядов, |
- плотность тока проводимости. |
||||||||||||
j |
|||||||||||||
Содержание этих уравнений заключается в следующем:
4
1. Циркуляция вектора |
|
по любому замкнутому контуру равна со знаком минус |
E |
производной по времени от магнитного потока через любую поверхность, ограниченную
данным контуром. При этом под |
|
понимается не только вихревое электрическое поле, |
E |
но и электростатическое. Это уравнение является, по существу, выражением закона электромагнитной индукции.
2. Поток вектора |
|
сквозь произвольную поверхность всегда равен нулю. Это |
B |
уравнение указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов.
3. Циркуляция вектора |
|
по любому замкнутому контуру равна полному току (току |
H |
проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром.
|
|
|
|
|
|
|
|
4. |
Поток вектора D |
сквозь любую замкнутую поверхность равен алгебраической |
|||||
сумме сторонних зарядов, охватываемых этой поверхностью. |
|
|
|
|
|||
Из |
уравнений (9.12) |
и (9.14) для циркуляции векторов |
и |
следует, что |
|||
E |
H |
||||||
электрическое и магнитное поле взаимосвязаны: изменение во времени одного из этих полей приводит к появлению другого. Поэтому имеет смысл лишь совокупность этих полей, описывающая единое электромагнитное поле.
|
|
|
Если же поля стационарны ( E const |
и |
B |
распадаются на две группы независимых уравнений:
|
|
|
|
Edl |
0 ; |
BdS |
0 |
Hdl jdS ; |
|
DdS dV |
|
const
),
то уравнения Максвелла
(9.16)
В этом случае электрическое и магнитное поля независимы друг от друга. |
|
|||||||||
Уравнения (9.12) – (9.15) в дифференциальной форме имеют вид: |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|||
|
B |
|
|
|
|
|||||
rotE |
|
t |
, |
или |
E |
t |
(9.17) |
|||
|
|
|
|
|||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
B 0 |
|
|
||||
divB |
, |
|
или |
|
(9.18) |
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
rotH j D |
|
H j D |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
, или |
|
|
|
t |
(9.19) |
|
|
|
|
|
|
|
|
|||
divD , |
|
или |
D |
|
|
(9.20) |
||||
Чтобы осуществить расчет полей E и B по уравнениям (9.17) – (9.20) нужно дополнить их уравнениями:
|
|
|
|
|
D 0 E , |
|
(9.21) |
||
|
|
|
, |
(9.22) |
B |
0 H |
|||
|
|
|
|
|
j |
E |
, |
|
(9.23) |
где , , - известные нам постоянные, характеризующие электрические и магнитные
свойства среды (диэлектрическая и магнитная проницаемости и электропроводность). Уравнения (9.17) – (9.23) образуют основу электродинамики покоящихся сред.
5

4 Свойства уравнений Максвелла
1 О симметрии уравнений Максвелла
В нейтральной |
однородной непроводящей среде, где |
0 |
и |
|
0 |
, уравнения |
||||||||||
j |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
, как |
|
E |
: |
|
|
|||
Максвелла приобретают симметричный вид, т.е. E так связано с |
t |
|
B с |
t |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
B |
|
|
|
|
|
|
|
|
|
|
||||
rotE |
|
t |
|
, |
divB 0 , |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
||||
rotH |
t |
, |
|
divD 0 |
|
|
|
|
|
|
(9.24) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Различие в знаках перед производными показывает, что силовые линии вектора |
, |
|||||||||||||||
E |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
||
индуцированного изменением поля B , образуют с вектором |
левовинтовую систему, |
в |
||||||||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то время как линии магнитного поля H , индуцированного изменением |
D , |
образуют с |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектором |
D |
правовинтовую систему (рис. 2). |
|
|
|
|
|
|
|
|
|
|||||
t |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 2
2. Об электромагнитных волнах
Из уравнений Максвелла следует важный вывод: электромагнитное поле способно существовать самостоятельно – без электрических зарядов и токов.
При этом изменение состояния поля имеет волновой характер. Поля такого рода называют электромагнитными волнами. В вакууме они всегда распространяются со
скоростью, равной скорости света |
с . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|||
Ток смещения |
|
|
|
играет в этом явлении основную роль. Именно его присутствие |
||||||||
|
t |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
B |
и означает возможность появления электромагнитных волн. |
|||||||
наряду с величиной |
|
|
||||||||||
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Всякое |
изменение |
во времени магнитного |
|
поля |
|
B |
возбуждает поле |
|||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
электрическое |
, изменение же поля электрического |
|
E |
|
|
|
||||||
E |
|
, в свою очередь, возбуждает |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
магнитное поле B . В результате такое электромагнитное возмущение распространяется в пространстве (рис. 3).
6

Рис. 3
Теория Максвелла не только предсказала возможность существования электромагнитных волн, но и позволила установить все их основные свойства:
1) скорость распространения электромагнитных волн в среде
v |
c |
, где c |
|
|
1 |
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
0 |
|
|||
2) векторы |
, |
и |
|
|
(скорость волны) |
|||||
E |
B |
|
v |
|||||||
правовинтовую систему (рис. 4)
(9.25)
взаимно перпендикулярны и образуют
Рис. 4
3) в электромагнитной волне векторы |
|
и |
|
всегда колеблются в одинаковых фазах |
E |
B |
(рис. 5, где показана мгновенная «фотография» волны), причем между мгновенными
значениями E и |
B в любой точке существует определенная связь: |
|
|||
|
|
|
|
|
|
|
0 E |
0 H |
(9.26) |
||
7
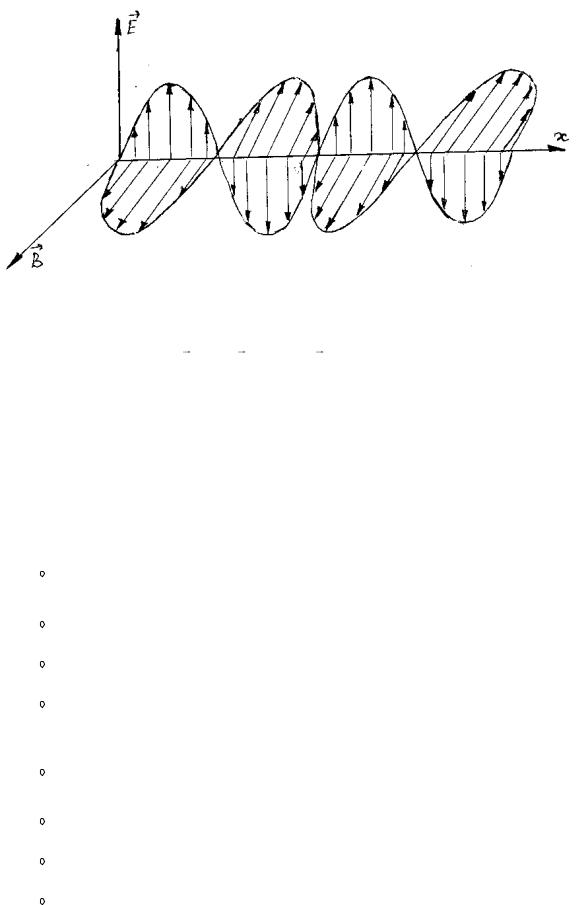
Рис. 5
Это значит, что |
E |
и |
H |
одновременно обращаются в нуль и Электромагнитные волны и их
(или т.д. свойства
B ) одновременно достигают максимума,
будут рассмотрены далее в главе 11.
Тесты
1. Полная система уравнений Максвелла для электромагнитного поля имеет вид:
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
||||
Edl |
t |
dS |
|
|
||||
L |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
D |
|||||
|
|
|
|
|
|
|
|
|
|
Hdl |
|
j |
|
|
|
||
|
|
t |
dS |
|||||
L |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|||
DdS dV
S V
BdS 0
S
Следующая система уравнений:
|
|
|
|
|
|
|
|
|
B |
||||||
Edl |
t |
dS |
|||||
L |
|
|
S |
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
D |
|
|||||
Hdl |
|
t |
dS |
||||
L |
|
S |
|
|
|
||
|
|
|
|
|
|
||
DdS 0
S
BdS 0
S
8

справедлива для переменного электромагнитного поля…
1)в отсутствие заряженных тел и токов проводимости
2)при наличии заряженных тел и токов проводимости
3)в отсутствие заряженных тел
4)в отсутствие токов проводимости
2. Полная система уравнений Максвелла для электромагнитного поля имеет вид:
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
||||
Edl |
t |
dS |
|
|
||||
L |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
D |
||||||
|
|
|
|
|
|
|
|
|
|
Hdl |
|
j |
|
|
|
||
|
|
t |
dS |
|||||
L |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|||
DdS dV
S |
|
V |
|
|
|
BdS |
0 |
|
S |
|
|
Эта система справедлива для переменного электромагнитного поля…
1) в отсутствие заряженных тел и токов проводимости
2) при наличии заряженных тел и токов проводимости
3)в отсутствие заряженных тел
4)в отсутствие токов проводимости
3. Полная система уравнений Максвелла для электромагнитного поля имеет вид:
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
||||
Edl |
t |
dS |
|
|
||||
L |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
D |
|||||
|
|
|
|
|
|
|
|
|
|
Hdl |
|
j |
|
|
|
||
|
|
t |
dS |
|||||
L |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|||
DdS dV
S |
|
V |
|
|
|
BdS |
0 |
|
S |
|
|
Следующая система уравнений:
Edl 0
L |
|
|
|
Hdl |
|
L |
|
|
|
DdS |
|
S |
|
BdS
S
jdS
dV
V
0
справедлива для …
1)стационарного электрического и магнитного полей
2)переменного электромагнитного поля при наличии заряженных тел и токов проводимости
3)переменного электрического поля в отсутствие заряженных тел
4)переменного электромагнитного поля в отсутствие токов проводимости
9

4. Полная система уравнений Максвелла для электромагнитного поля имеет вид:
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
||||
Edl |
t |
dS |
|
|
||||
L |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
D |
|||||
|
|
|
|
|
|
|
|
|
|
Hdl |
|
j |
|
|
|
||
|
|
t |
dS |
|||||
L |
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|||
DdS dV
S |
|
V |
|
|
|
BdS |
0 |
|
S |
|
|
Следующая система уравнений:
|
|
|
|
|
|
|
|
|
B |
|
|
||||
Edl |
t |
dS |
|
|
|||
L |
|
S |
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
||||||
Hdl |
|
|
|
D |
|
||
j |
t |
dS |
|||||
L |
|
S |
|
|
|
|
|
DdS 0
S
BdS 0
S
справедлива для переменного электромагнитного поля…
1) в отсутствие заряженных тел и токов проводимости
2) при наличии заряженных тел и токов проводимости
3) в отсутствие токов проводимости
4) в отсутствие заряженных тел
5. Полная система уравнений Максвелла для электромагнитного поля имеет вид:
|
|
|
|
|
|
|
|
|
B |
|
|
||||
Edl |
t |
dS |
|
|
|||
L |
|
S |
|
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
||||||
Hdl |
|
|
|
D |
|
||
j |
t |
dS |
|||||
L |
|
S |
|
|
|
|
|
DdS dV
S |
V |
BdS 0
S
Следующая система уравнений:
|
|
|
|
|
|
|
|
|
B |
||||||
Edl |
t |
dS |
|||||
L |
|
|
S |
|
|
||
|
|
|
|
|
|
||
|
|
D |
|
||||
Hdl |
|
t |
dS |
||||
L |
|
S |
|
|
|
||
|
|
|
|
|
|||
|
dV |
|
|||||
DdS |
|
||||||
S |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
BdS |
0 |
|
|
|
|
|
|
S
справедлива для переменного электромагнитного поля…
10
