+ |
− |
− |
|
+ |
|
−1 |
1 |
3 |
y′ |
|
max |
разрыв |
min |
|
|
|
Рис. 3.2.6. |
|
|
Из рисунка ясно, что функция имеет максимум в точке x1 = −1 и минимум в точке x2 = 3 . В точке разрыва характер монотонности не меняется.
3.2.2. Исследование функций с помощью второй производной. Точки перегиба
Определение 3.2.4
Функция f (x) называется выпуклой вниз (выпуклой) на промежутке (a,b), если ее
график лежит выше касательной, проведенной в любой точке x0 (a, b) (рис. 3.2.7 a).
Определение 3.2.5
Функция f (x) называется выпуклой вверх (вогнутой) на промежутке (a, b), если ее
график лежит ниже касательной, проведенной в любой точке x0 (a, b) (рис. 3.2.7 b).
|
|
y |
|
a |
x0 |
b |
x |
|
|
Рис. 3.2.7 a. |
|
y
a |
x0 |
b |
x |
|
Рис. 3.2.7 b. |
|
|
Теорема 3.2.1 |
|
Если функция f (x) |
дважды дифференцируема на промежутке (a, b) и вторая |
производная f ''(x)> 0 |
для всех значений x (a, b), то f (x) выпукла вниз на |
промежутке (a, b). |
|
Доказательство
1) Возьмем произвольную точку x0 (a, b). Уравнение касательной к графику функции в этой точке имеет вид:
y = f (x0 )+ f ′(x0 ) (x − x0 ).
Покажем, что в любой точке x (a, b) график функции расположен выше этой касательной.
Рассмотрим любую точку x (a, b), удовлетворяющую условию x > x0 , и вычислим разность ординат функции (f (x)) и касательной (y) в этой точке:
f (x)− y = f (x)−(f (x0 )+ f ′(x0 ) (x − x0 ))= (f (x)− f (x0 ))− f ′(x0 ) (x − x0 ).
Поскольку функция f (x) удовлетворяет условиям теоремы Лагранжа на промежутке (x0 , x), то найдется точка c1 (x0 , x), для которой справедливо равенство
f (x)− f (x0 )= f ′(c1) (x − x0 ).
Учитывая это, разность ординат функции и касательной в точке x можно представить в виде
40
f (x)− y = f ′(c1) (x − x0 )− f ′(x0 ) (x − x0 )= (f ′(c1 )− f ′(x0 )) (x − x0 ).
Производная |
′ |
f (x) удовлетворяет условиям теоремы Лагранжа на промежутке |
(x0 , с1). Значит, найдется точка c2 (x0 , с1), для которой справедливо равенство
f ′(c1)− f ′(x0 )= f ′′(c1) (с1 − x0 ).
Учитывая это, разность ординат функции и касательной в точке x можно записать в виде
|
|
|
|
f (x)− y = f ′′(c2 ) (c1 − x0 ) (x − x0 ). |
|
|
||||
Так как |
f ′′(x)> 0 при |
всех |
x (a,b), |
а x0 < c2 < c1 < x (рис. 3.2.8), то |
f ′′(с2 )> 0 |
, |
||||
c1 − x0 > 0 |
и x − x0 > 0 . |
Следовательно, |
f (x)− y > 0 |
и график функции в точке x > x0 |
||||||
расположен выше касательной. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
c |
c |
x |
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
Рис. 3.2.8. |
|
|
|
|
2) Рассмотрим любую |
точку |
x (a, b), удовлетворяющую условию |
x < x0 , |
и |
||||||
вычислим разность ординат функции (f (x)) и касательной (y) в этой точке: |
|
|
||||||||
f (x)− y = f (x)−(f (x0 )+ f ′(x0 ) (x − x0 ))= (f (x)− f (x0 ))− f ′(x0 ) (x − x0 )= |
|
|||||||||
|
|
= −(f (x0 )− f (x))+ f ′(x0 ) (x0 − x). |
|
|
||||||
Поскольку функция |
f (x) удовлетворяет условиям теоремы Лагранжа на промежутке |
|||||||||
(x, x0 ), то найдется точка c1 (x, x0 ), для которой справедливо равенство
f (x0 )− f (x)= f ′(c1 ) (x0 − x).
Учитывая это, разность ординат функции и касательной в точке x можно записать в виде f (x)− y = − f ′(c1 ) (x0 − x)+ f ′(x0 ) (x0 − x)= (f ′(x0 )− f ′(c1 )) (x0 − x).
Производная |
′ |
f (x) удовлетворяет условиям теоремы Лагранжа на промежутке |
(с1, x0 ). Значит, найдется точка c2 (с1, x0 ), для которой справедливо равенство
f ′(x0 )− f ′(c1)= f ′′(c2 ) (x0 −c1).
Учитывая это, разность ординат функции и касательной в точке x можно записать в виде
|
|
f (x)− y = f ′′(c2 ) (x0 −c1 ) (x0 − x). |
|
Так как |
f ′′(x)> 0 при |
всех x (a,b), |
а x < c1 < c2 < x0 (рис. 3.2.9), то f ′′(с2 )> 0 , |
x0 −c1 > 0 |
и x0 − x > 0 . |
Следовательно, |
f (x)− y > 0 . Тогда график функции в точке |
x < x0 также расположен выше касательной.
x |
c1 |
c2 |
x0 |
|
Рис. 3.2.9. |
|
|
Теорема 3.2.2 |
|
|
|
Если функция f (x) дважды |
дифференцируема |
на промежутке (a,b) и вторая |
|
′′ |
|
f (x) на промежутке (a,b) выпукла вверх. |
|
производная f (x)< 0 для всех x (a,b), то |
|||
Доказательство
аналогично доказательству теоремы 1.
41
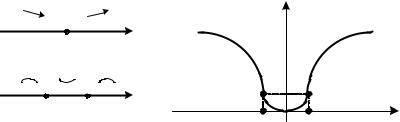
Определение 3.2.6
Точки, в которых меняется характер выпуклости функции, называются точками перегиба.
Теорема 3.2.3
Если f ′′(x0 )= 0 и f ′′(x) меняет знак при переходе через точку x0 , то функция f (x) имеет в точке x0 перегиб.
ЗАМЕЧАНИЕ
Вторая производная может менять знак и в точке разрыва. Поэтому точками перегиба являются точки, в которых вторая производная обращается в ноль или бесконечна (а функция определена) и меняет знак.
Чтобы найти точки перегиба графика функции нужно:
•вычислить вторую производную заданной функции;
•найти все точки, в которых вторая производная равна нулю или не существует;
•нанести эти точки, а также точки разрыва функции на числовую ось;
•определить знак второй производной на каждом из полученных интервалов;
•по знаку второй производной определить характер выпуклости функции;
•точками перегиба будут те точки, в которых меняется характер выпуклости функции, исключая точки разрыва.
Задача 3.2.4
Определите точки перегиба графика функции f (x)= ln(x2 +1).
Решение
|
|
|
|
|
|
′ |
1 |
|
|
|
Исследуя первую |
||
|
|
|
|
|
|
|
|
|
|
|
|||
Первая производная заданной функции равна f (x)= x2 +1 2x . |
|||||||||||||
производную легко убедиться, что функция имеет минимум в точке |
x = 0 |
. |
|||||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
y = 0 |
|
||
Теперь вычислим вторую производную |
|
|
|
|
|
|
|
|
|
|
|||
y′′ = 2 |
x2 |
+1− x 2x |
= 2 |
|
1− x2 |
2 (1− x) (1+ x) |
|
|
|||||
|
|
|
= |
|
|
|
|
|
|||||
|
(x2 +1)2 |
(x2 +1)2 |
(x2 +1)2 |
|
|
|
|
||||||
и исследуем ее. Вторая производная меняет знак в точках x = ±1. По знаку второй производной y′′ можно выяснить характер выпуклости функции (рис. 3.2.10).
|
− |
+ |
|
y |
|
|
y′ |
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
− |
+ |
− |
y′′ |
ln 2 |
|
|
−1 |
1 |
|
|
|
|
|
−1 0 1 |
x |
||
перегиб |
перегиб |
|
|||
Рис. 3.2.10.
x
Из рисунка видно, что функция имеет две точки перегиба
y
показан график заданной функции.
=±1
=ln 2 . На рисунке 17
42