
- •Санкт-петербургский государственный морской технический университет
- •Задание
- •Содержание
- •1. Одномерная оптимизация 4
- •2. Многомерная оптимизация 14
- •1. Одномерная оптимизация
- •1.1 Метод Свенна
- •1.2 Метод равномерного поиска
- •1.3 Метод дихотомии
- •1.4 Метод золотого сечения
- •1.5 Метод Фибоначчи
- •2. Многомерная оптимизация
- •2.1 Метод Коши
- •2.2. Метод Ньютона.
- •Список использованной литературы
1.5 Метод Фибоначчи
Найти
минимум функции
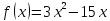 методом Фибоначчи с точностью
методом Фибоначчи с точностью
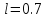 ,
начальной точкой
,
начальной точкой
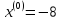 и константой различимости
и константой различимости
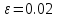 .
.
Решение:
1. Начальный интервал неопределенности [a0; b0] = [-2;22].
2. Найдем числа Фибоначчи:
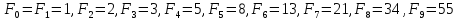
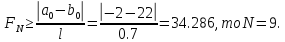
3.
Предположим, что
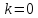 ;
;
4. Вычислим :
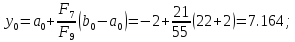

5.
Вычислим
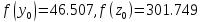 (рисунок 1,5).
(рисунок 1,5).
6.
Сравним
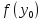 и
и
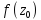 .
Так как
.
Так как
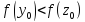 ,
то
,
то
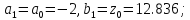
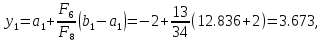
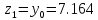 .
.
7. Проверим условие окончания:
 следовательно,
следовательно,
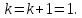 Переходим к шагу 51.
Переходим к шагу 51.
51.
Вычислим
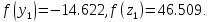
61.
Сравним
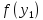 и
и
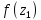 .
Так как
.
Так как
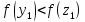 ,
то
,
то
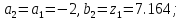
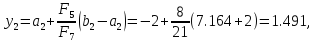
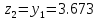 .
.
71. Проверим условие окончания:
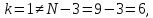 следовательно,
следовательно,
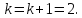 Переходим к шагу 52.
Переходим к шагу 52.
52.
Вычислим
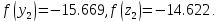
62.
Сравним
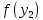 и
и
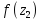 .
Так как
.
Так как
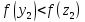 ,
то
,
то
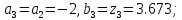
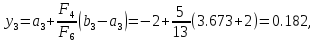
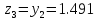 .
.
72. Проверим условие окончания:
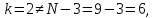 следовательно,
следовательно,
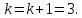 Переходим к шагу 53.
Переходим к шагу 53.
53.
Вычислим
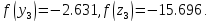
63.
Сравним
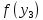 и
и
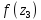 .
Так как
.
Так как
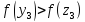 ,
то
,
то
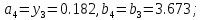
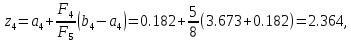
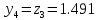 .
.
73. Проверим условие окончания:
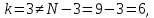 следовательно,
следовательно,
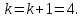 Переходим к шагу 54.
Переходим к шагу 54.
54.
Вычислим
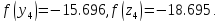
64.
Сравним
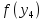 и
и
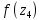 .
Так как
.
Так как
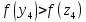 ,
то
,
то
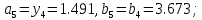
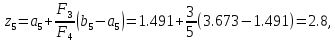
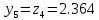 .
.
74. Проверим условие окончания:
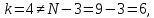 следовательно,
следовательно,
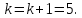 Переходим к шагу 55.
Переходим к шагу 55.
55.
Вычислим
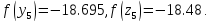
65.
Сравним
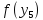 и
и
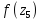 .
Так как
.
Так как
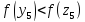 .
, то
.
, то
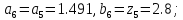
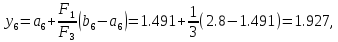
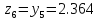 .
.
75. Проверим условие окончания:
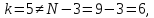 следовательно,
следовательно,
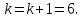 Переходим к шагу 56.
Переходим к шагу 56.
56.
Вычислим
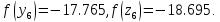
66.
Сравним
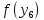 и
и
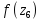 .
Так как
.
Так как
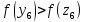 ,
то
,
то
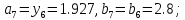
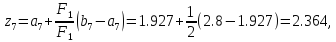
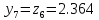 .
.
76. Проверим условие окончания:
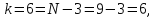 y7
= z7
=
y7
= z7
=
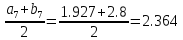 ,
то
,
то
y8 = y7 = z7 =2.364
z8 = y8 + ε = 2.364 + 0.02 = 2.366
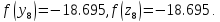
Так
как
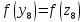 ,
то
,
то
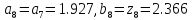
Поэтому
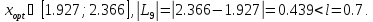
В качестве приближенного решения возьмем середину полученного интервала:
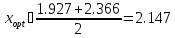
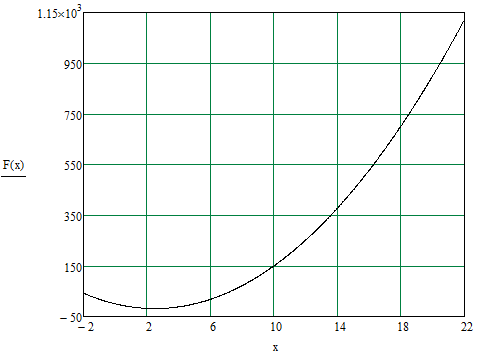
Рисунок 1.5 - Первые итерации поиска методом Фибоначчи
2. Многомерная оптимизация
2.1 Метод Коши
Найти минимум функции Ф(x) = (x1 + 2x2)2 + (x2 - 4)2 методом Коши с точностью ε = 0.3 для начальной точки с координатами x(0) = (- 4; 7).
Решение:
1.Предположим k = 0.
2.Вычислим компоненты градиента :
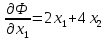

Т.е.
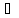 Ф(
Ф(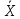 )
= (
)
= (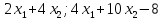 )
)
3. Вычислим :
 Ф(x(0))
= (
Ф(x(0))
= (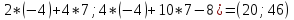
Так
как |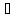 Ф(x(0))
| =
Ф(x(0))
| =
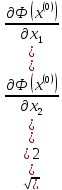 ,
то переходим к шагу 4.
,
то переходим к шагу 4.
4.
С помощью формулы
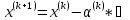 Ф(x(k))
построим первое приближение:
Ф(x(k))
построим первое приближение:
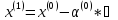 Ф(x(0))
Ф(x(0))
Выберем
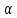 таким образом, чтобы минимизировать
функцию по
таким образом, чтобы минимизировать
функцию по
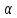 :
:
Ф(x(1))→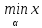
Ф(x)
=
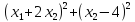
ε = 0.3
x(0) = (- 4; 7).
Определяем
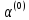 :
:
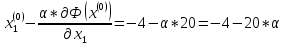
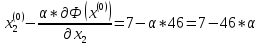
Ищем параметр :
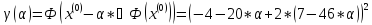 +
+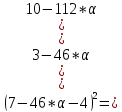
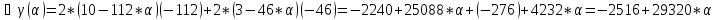
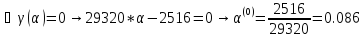
Поскольку
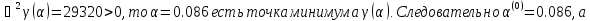
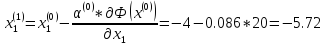
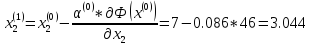
Т.е. x(1) = (- 5.72; 3.04)
5. Вычислим :
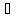 Ф(x(1))
= (
Ф(x(1))
= (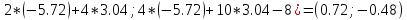
Так
как |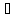 Ф(x(1))
| =
Ф(x(1))
| =
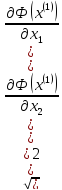 ,
то
,
то
k
= k+1
=1 переходим к шагу
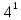 .
.
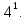 Определяем
Определяем
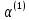 :
:
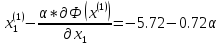
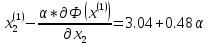
Ищем параметр :
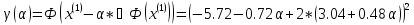 +
+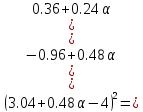
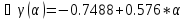
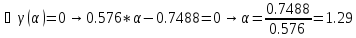
Поскольку
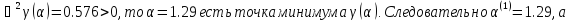
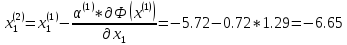
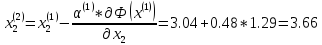
Т.е. x(2) = (- 6.65; 3.66)
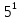 .
Вычислим :
.
Вычислим :
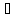 Ф(x(2))
= (
Ф(x(2))
= (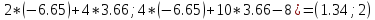
Так
как |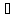 Ф(x(2))
| =
Ф(x(2))
| =
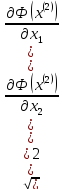 ,
то
,
то
k
= k+1
=2 переходим к шагу
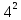 .
.
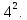 Определяем
Определяем
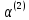 :
:
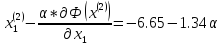
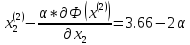
Ищем параметр :
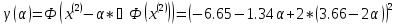 +
+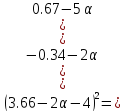
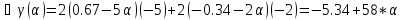
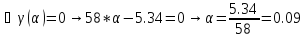
Поскольку
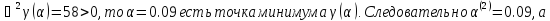
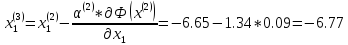
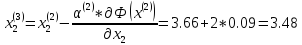
Т.е. x(3) = (- 6.77; 3.48)
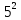 .
Вычислим :
.
Вычислим :
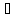 Ф(x(3))
= (
Ф(x(3))
= (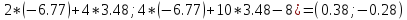
Так
как |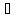 Ф(x(3))
| =
Ф(x(3))
| =
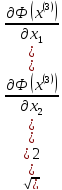 ,
то
,
то
k
= k+1
=3 переходим к шагу
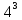 .
.
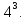 Определяем
Определяем
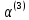 :
:
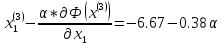
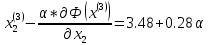
Ищем параметр :
 +
+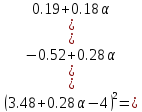
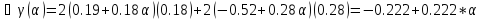
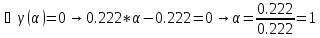
Поскольку
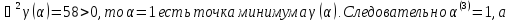
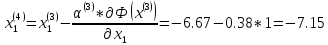
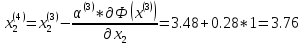
Т.е. x(4) = (- 7.15; 3.76)
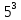 .
Вычислим :
.
Вычислим :
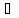 Ф(x(4))
= (
Ф(x(4))
= (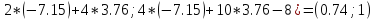
Так
как |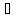 Ф(x(4))
| =
Ф(x(4))
| =
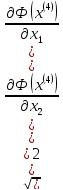 ,
то
,
то
k
= k+1
=4 переходим к шагу
 .
.
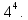 Определяем
Определяем
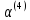 :
:
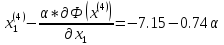
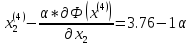
Ищем параметр :
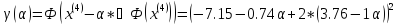 +
+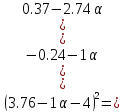
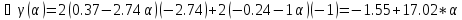
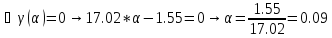
Поскольку
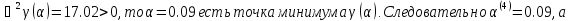
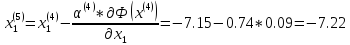
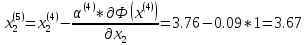
Т.е. x(5) = (- 7.22; 3.67)
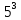 .
Вычислим :
.
Вычислим :
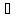 Ф(x(5))
= (
Ф(x(5))
= (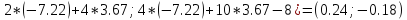
Так
как |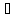 Ф(x(5))
| =
Ф(x(5))
| =
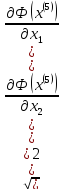 ,
то
,
то
вычисления завершаются.
В результате решения задачи безусловной многомерной оптимизации получаем:
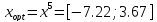 (рисунок
2.2)
(рисунок
2.2)
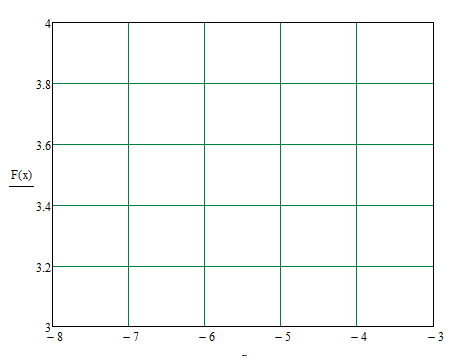
Рисунок 2.2 – Траектория спуска
