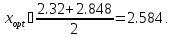- •Санкт-петербургский государственный морской технический университет
- •Задание
- •Содержание
- •1. Одномерная оптимизация 4
- •2. Многомерная оптимизация 14
- •1. Одномерная оптимизация
- •1.1 Метод Свенна
- •1.2 Метод равномерного поиска
- •1.3 Метод дихотомии
- •1.4 Метод золотого сечения
- •1.5 Метод Фибоначчи
- •2. Многомерная оптимизация
- •2.1 Метод Коши
- •2.2. Метод Ньютона.
- •Список использованной литературы
1.2 Метод равномерного поиска
Найти
минимум функции
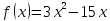 методом равномерного поиска.
методом равномерного поиска.
Решение:
1.
Зададим
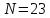 так, чтобы
так, чтобы
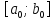 содержал
содержал
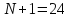 равных подынтервалов.
равных подынтервалов.
2.
Определим точки вычисления функции:
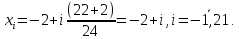
3. Вычислим значения функции в двадцати трех точках:
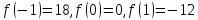 .
.
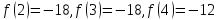 .
.
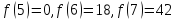
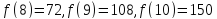 .
.
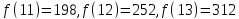 .
.
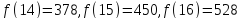 .
.
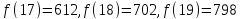
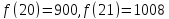
4.
В точке
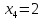 функция
принимает наименьшее значение:
функция
принимает наименьшее значение:
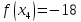 .
.
5.
Искомая точка минимума после двадцати
трех вычислений принадлежит интервалу:
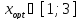 ,
в котором выбирается точка
,
в котором выбирается точка
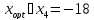 (рисунок 1.2)
(рисунок 1.2)
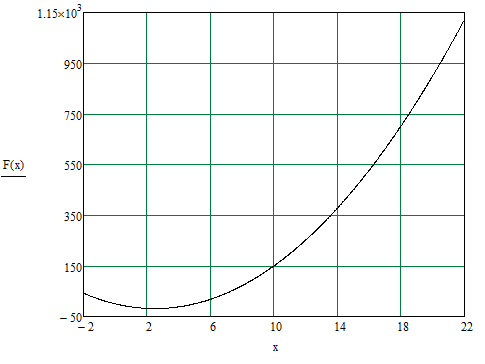
Рисунок 1.2 - Точка минимума заключенная в найденном интервале
1.3 Метод дихотомии
Найти
минимум функции
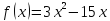 методом дихотомии с точностью
методом дихотомии с точностью
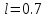 ,
начальной точкой
,
начальной точкой
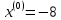 и константой различимости
и константой различимости
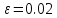 .
.
Решение:
1. Начальный интервал неопределенности [a0; b0] = [-2;22].
2.
Предположим, что
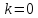 .
.
3. Вычислим
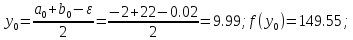
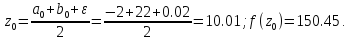
4.Сравниваем две функции :
Так
как
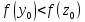 ,
то
,
то
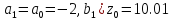 и переходим к шагу 5
и переходим к шагу 5
(рисунок 1.3)
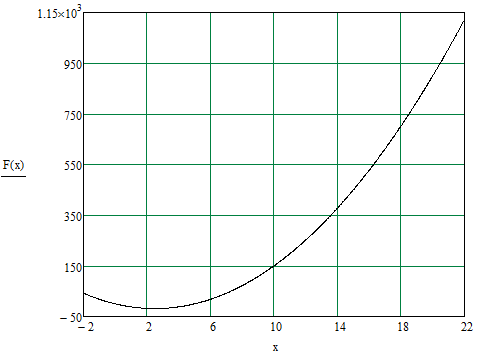
Рисунок 1.3 - Первые итерации поиска методом дихотомии
5.
Получим
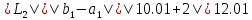 ,
поскольку
,
поскольку
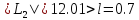 ,
,
то
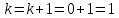 и переходим к шагу 31.
и переходим к шагу 31.
31. Вычислим
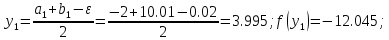
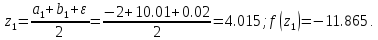
41. Сравниваем две функции :
Так
как
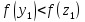 ,
то то
,
то то
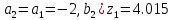 и переходим к шагу 51
и переходим к шагу 51
51.
Получим
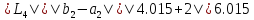 ,
,
Так
как
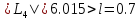 ,
то
,
то
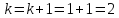 и переходим к шагу 32.
и переходим к шагу 32.
32. Вычислим :
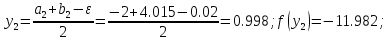
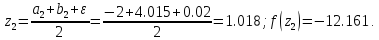
42. Сравниваем две функции :
Так
как
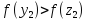 ,
то
,
то
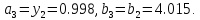
52.
Получим
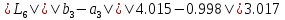 ,
поскольку
,
поскольку
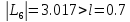 ,
,
то
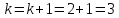 и переходим к шагу 33.
и переходим к шагу 33.
33. Вычислим :
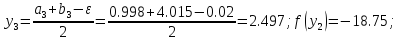
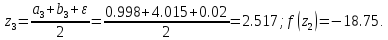
43. Сравниваем две функции :
Так
как
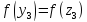 ,
то
,
то
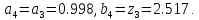
53.
Получим
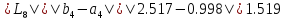 ,
поскольку
,
поскольку
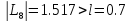 ,
,
то
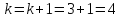 и переходим к шагу 34.
и переходим к шагу 34.
34. Вычислим :
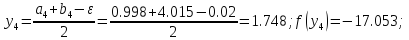
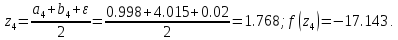
44. Сравниваем две функции :
Так
как
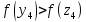 ,
то
,
то
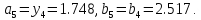
54.
Получим
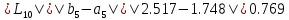 ,
,
поскольку
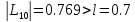 ,
то
,
то
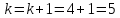 и переходим к шагу 35.
и переходим к шагу 35.
35. Вычислим :
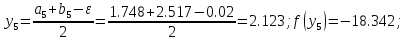
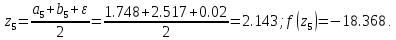
45. Сравниваем две функции :
Так
как
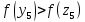 ,
то
,
то
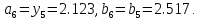
55.
Получим
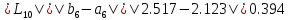 ,
,
поскольку
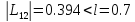 ,
то вычисления прекращаются и
,
то вычисления прекращаются и
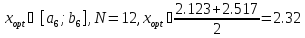
1.4 Метод золотого сечения
Найти
минимум функции
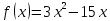 методом золотого сечения с точностью
методом золотого сечения с точностью
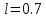 ,
начальной точкой
,
начальной точкой
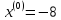 .
.
Решение:
1. Начальный интервал неопределенности [a0; b0] = [-2;22].
2.
Предположим, что
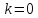 ;
;
3. Вычислим:
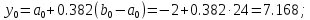
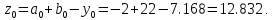
4. Вычислим функцию в двух точках:
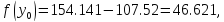
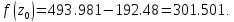
5.Проверяем :
Так
как
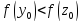 ,
то
,
то
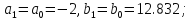
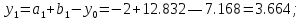
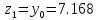
(рисунок 1.4).
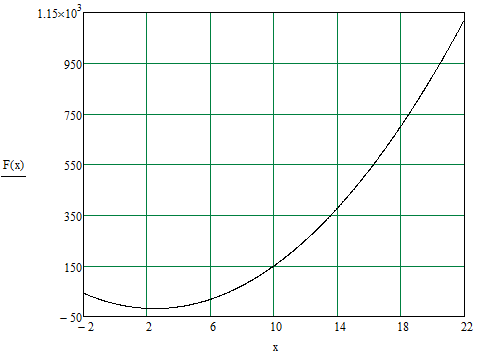
Рисунок 1.4 - Первые итерации поиска методом золотого сечения
6. Вычисляем :
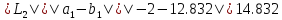 ,
поскольку
,
поскольку
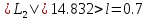 ,
,
то
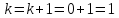 и переходим к шагу 41.
и переходим к шагу 41.
41. Вычислим функцию в двух точках:
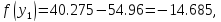
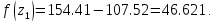
51.Проверяем :
Так
как
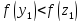 ,
то
,
то
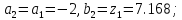
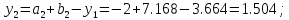
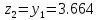
61. Вычисляем :
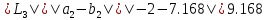 ,
поскольку
,
поскольку
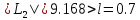 ,
,
то
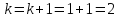 и переходим к шагу 42.
и переходим к шагу 42.
42. Вычислим функцию в двух точках:
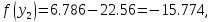
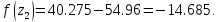
52.Проверяем :
Так
как
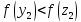 ,
то
,
то
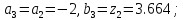
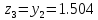
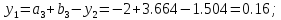
62. Вычисляем :
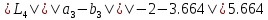 ,
поскольку
,
поскольку
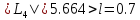 ,
,
то
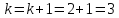 и переходим к шагу 43.
и переходим к шагу 43.
43. Вычислим функцию в двух точках:
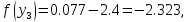
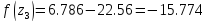
53.Проверяем :
Так
как
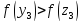 ,
то
,
то
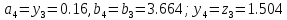
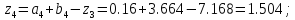
63. Вычисляем :
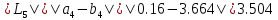 ,
поскольку
,
поскольку
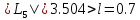 ,
,
то
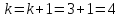 и переходим к шагу 44.
и переходим к шагу 44.
44. Вычислим функцию в двух точках:
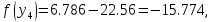
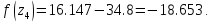
54.Проверяем :
Так
как
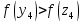 ,
то
,
то
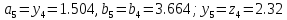
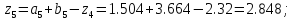
64. Вычисляем :
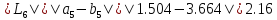 ,
поскольку
,
поскольку
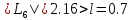 ,
,
то
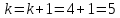 и переходим к шагу 45.
и переходим к шагу 45.
45. Вычислим функцию в двух точках:
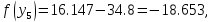
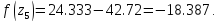
55.Проверяем :
Так
как
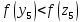 ,
то
,
то
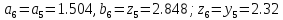
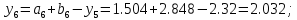
65. Вычисляем :
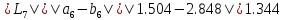 ,
поскольку
,
поскольку
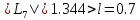 ,
,
то
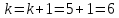 и
переходим к шагу 46.
и
переходим к шагу 46.
46. Вычислим функцию в двух точках:
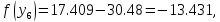
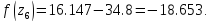
56.Проверяем :
Так
как
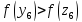 ,
то
,
то
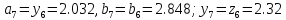
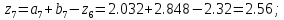
66. Вычисляем :
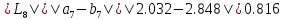 ,
поскольку
,
поскольку
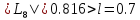 ,
,
то
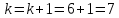 и переходим к шагу 47.
и переходим к шагу 47.
47. Вычислим функцию в двух точках:
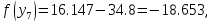
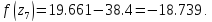
57.Проверяем :
Так
как
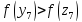 ,
то
,
то
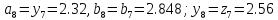
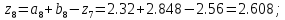
67. Вычисляем :
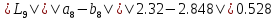 ,
поскольку
,
поскольку
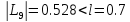 ,
,
то вычисления прекращаются и