Санкт-петербургский государственный морской технический университет

_____________________________________________________________________________________________

Факультет МОРСКОГО ПРИБОРОСТРОЕНИЯ

Кафедра самоходных подводных аппаратов (№30)

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К КУРСОВОЙ РАБОТЕ

ПО ДИСЦИПЛИНЕ

«ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ»

ВЫПОЛНИЛ __________ Ахрестин А. А.

^{подпись}

ПРОВЕРИЛА __________ Миннуллина Ю. З.

^{подпись}

ДАТА ЗАЩИТЫ ______________

ОЦЕНКА ______________

2012 г.

Задание

Вариант №7 по теме "Одномерная оптимизация": для заданной функции

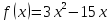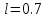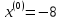с точностью , начальной точкой и константой различимости 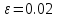найти:

1. Начальный интервал неопределенности методом Свенна;

2. Минимум функции методом равномерного поиска;

3. Минимум функции методом дихотомии;

4. Минимум функции методом золотого сечения;

5. Минимум функции методом Фибоначчи.

Вариант №15 по теме "Многомерная оптимизация": для заданной функции

Ф(x) = (x₁ + 2x₂)² + (x₂ - 4)² найти минимум с точностью ε = 0.3 для начальной точки с координатами x⁽⁰⁾ = (- 4; 7).

1. Методом Коши.

2. Методом Ньютона.

Содержание

1. Одномерная оптимизация 4

1.1 Метод Свенна 4

1.2 Метод равномерного поиска 5

1.3 Метод дихотомии 6

1.4 Метод золотого сечения 8

1.5 Метод Фибоначчи 12

2. Многомерная оптимизация 14

2.1 Метод Коши 14

2.2 Метод Ньютона 19

1. Одномерная оптимизация

1.1 Метод Свенна

Найти начальный интервал неопределенности для функции 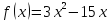методом Свенна с начальной точкой .

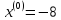Решение:

1. Зададим шаг 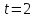. предположим, что ;

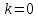2. Вычислим значение функции в трех точках:

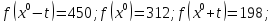
3. Проверяем условие окончания:

Т.к 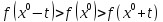, то переходим к шагу 4.

4. Определяем величину ∆ (дельта):

a) Функция 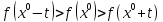, то ∆ = t = 2, a₀ = x₀ = - 8, x₁ = x₀ + t = - 6, k = 1.

5. Находим следующую точку:

x^k+1 = x² → x² = x¹ + 2¹*∆ = - 6 + 2*2 = - 2.

6. Проверяем условие убывания функции:

a)

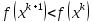
3*(- 2)² – 15*(- 2) < 3*(- 6)²- 15*(- 6)

42 < 198

∆= t→ a₀ = x^k+1= -2 и переходим к шагу 5

k = 2

x^k+1 = x³ → x³= x² + 2²*∆ = -2 + 4*2 = 6

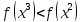
18 < 42 → переходим к шагу 5

k = 3

x^k+1 = x⁴ → x⁴= x³ + 2³*∆=6 + 8*2 = 22

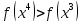
1122 > 18 → ∆ = t → b₀ = x^k+1= x⁴=22

Начальный интервал неопределенности методом Свенна найден:

[a₀; b₀] = [-2;22] (рисунок 1.1).

Рисунок 1.1 - Найденный интервал неопределенности