8 Закон взаимосвязи массы и энергии

Рассмотрим кинетическую энергию релятивистской частицы. Определим эту величину таким же путем, как в классической физике:

.

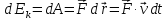Согласно основному уравнению релятивистской динамики (16)

,

, где – релятивистская масса.

Поэтому

Упростим это выражение, используя формулу для релятивистской массы

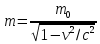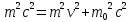. Приведем ее к виду , гдеи.

Найдем дифференциал этого выражения

.

Разделим на , получим

.

Отсюда следует

. (17)

Таким образом, приращение кинетической энергии частицы пропорционально приращению ее релятивистской массы. Для покоящейся частицы , а. Поэтому, интегрируя (17), получим

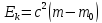, (18)

или

. (19)

Это и есть выражение для релятивистской кинетической энергии частицы. Убедимся, что при малых скоростях выражение (19) переходит в ньютоновское. Для этого воспользуемся формулой бинома Ньютона, согласно которой

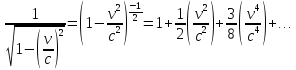
Тогда

.

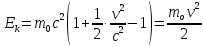Перепишем соотношение (18) в такой форме:

.

Здесь - (20)

- энергия покоя частицы,

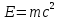
-полная энергия частицы

Отсюда 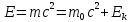(22)

-закон взаимосвязи массы и энергии.

Видно, что масса тела, которая в классической физике выступала как мера инертности (во втором законе Ньютона) или как мера гравитационного взаимодействия (в законе всемирного тяготения), теперь выступает в новой функции – как мера энергосодержания тела.

Всякое изменение энергии тела сопровождается изменением релятивистской массы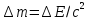, и наоборот, всякое изменение массысопровождается изменением энергии тела.

В ядерной физике впервые оказалось возможным экспериментально проверить и подтвердить закон взаимосвязи массы и энергии.

Формулы (20)-(22) – знаменитые формулы Эйнштейна, устанавливающие эквивалентность массы и энергии.

9. Связь между энергией и импульсом частицы

Ясно, что полная энергия и импульсчастицы имеют разные значения в разных системах отсчета. Оказывается, однако, что существует величина – некоторая комбинацияи, которая является инвариантной, то есть имеет одно и то же значение в разных системах отсчета. Эта величина есть. Убедимся в этом.

Итак, и,.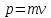

Запишем

,

или после сокращения

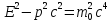(23)

Тот факт, что скорость 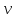в правой части сократилась, означает, что величина (не зависит от скорости частицы, а следовательно, и от системы отсчета.

Отсюда

. (24)

Приведем еще два полезных соотношения, с которыми приходится часто встречаться при решении задач в ядерной физике.

Первое:

, (25)

второе – связь между импульсом и кинетической энергией частицы. Подставим в формулу (23) , получим

(26)

Рассмотрим вопрос о возможности существования частиц с нулевой массой покоя . Из формул (24) и (25)

следует, что эти два выражения совместны, если .

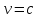Таким образом, согласно теории относительности существование частиц с нулевой массой покоя возможно, причем эти частицы могут двигаться только со скоростью света . Как сейчас известно, такими частицами являются фотон и нейтрино.

СТО находит подтверждение в экспериментах с элементарными частицами.

Однако СТО не дает возможности создать теорию гравитационного взаимодействия, не объясняет закон всемирного тяготения Ньютона.

Задачи

Задача 1. Серпуховский ускоритель разгоняет протоны до кинетической энергии

76 ГэВ. Найти массу и скорость ускоренных протонов.

Решение

, отсюда

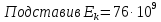эВ, эВ, получим.

найдем .

;

.

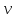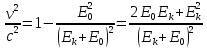Задача 2. Частица массы начинает двигаться под действием постоянной силы. Найти зависимость скорости частицы от времени.

Решение

, .

; .

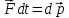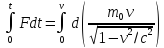
Отсюда

.

Согласно второму закону Ньютона 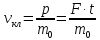,можно представить в виде:

Отсюда видно, что , т.е. скорость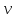частицы растет со временем медленнее, чем, причем при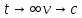(рис. )

Рис.

Задача3. Метод встречных пучков

Два протона движутся навстречу друг другу с одинаковыми кинетическими энергиями (в -системе отсчета). Найти кинетическую энергиюодного протона в-системе отсчета, где другой протон покоится.

Решение

Рис.1 Рис.2

Воспользуется инвариантностью величины ,

где

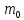–масса покоя протона.

Запишем выражение () в К -системе, а также в-системе.

В -системе (рис. 1) два протона движутся навстречу друг другу, поэтому

, (1)

(2)

В -системе (рис. 2) один протон покоится, а второй движется со скоростью, поэтому

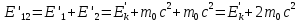(3)

. (4)

Итак,

,

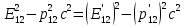После подстановки (1)-(4), получим

.

Отсюда

.

Для протона 939 МэВ1ГэВ. Например, при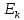= 50 ГэВ величинаГэВ. Возможность получения такого большого «выигрыша» в энергии лежит в основе принципа действия ускорителей на встречных пучках, которые называются коллайдерами.

25