Глава 2 Релятивистская динамика

6 Релятивистский импульс

Напомним сначала два основных положения ньютоновской механики об импульсе:

1) импульс частицы определяется как , где– масса частицы не зависит от ее скорости;

2) импульс замкнутой системы частиц сохраняется во времени в любой инерциальной системе отсчета.

В теории относительности за фундаментальный закон принимается именно закон сохранения импульса и уже отсюда находят выражение для самого импульса.

Предположим, в -системе отсчета частица с собственной массой (массой покоя)и наблюдатель в-системе может определить импульс этой частицы

,

где – характеризует перемещение частицы за время,– собственное время для частицы, для которой вычисляется импульс, то есть время по часам, движущимся вместе с частицей.

Рассмотрим абсолютно упругий удар в системах отсчета и. Пусть в системеимпульс системы сохраняется. Покажем, что он будет сохраняться в системе.

Итак, – масса покоя 1 частицы,– масса покоя 2 частицы, тогда

ЗСИ: .

В системе отсчета есть «часы», показывающие время, причем

.

Наблюдатель находится в К -системе отсчета, и для него ЗСИ:

или можно записать в виде:

. .

При этом мы обозначили

; .

В таком виде закон сохранения импульса выполняется.

А теперь напишем выражение для импульса релятивистской частицы. Перейдем в систему отсчета , относительно которой наблюдается движение частицы со скоростью.

,

где – скорость частицы.

Таким образом, релятивистский импульс

‘ (14)

где

(15)

масса движущейся частицы или релятивистская масса, – масса покоя.

Релятивистская масса частицы зависит от ее скорости и больше массы покоя (рис. 3).

Рис. 3

В отличие от релятивистской массы масса покоя – величина инвариантная, т.е. одинаковая во всех системах отсчета.

Опыт показывает, что так определенный импульс действительно подчиняется закону сохранения импульса независимо от выбора инерциальной системы отсчета.

При из (14) следует ньютоновское определение импульса:, гдене зависит от скорости. На рис.4 показаны для сравнения графики зависимостей релятивистскогои ньютоновскогоимпульсов частицы от скорости.

Рис. 4

Пример

В современных гигантских ускорителях протоны ускоряются до скоростей, отличающихся от скорости света на 0,0003%. Найдем, во сколько раз релятивистская масса таких протонов превышает их массу покоя.

Решение

Согласно(15) , где

Т.к. , то.

Тогда .

7 Основное уравнение релятивистской динамики

Согласно принципу относительности Эйнштейна, все законы природы должны быть инварианты по отношению к инерциальным системам отсчета. Уравнение Ньютона не удовлетворяет принципу относительности Эйнштейна.

Преобразования Лоренца при переходе к другой инерциальной системе придают ему совершенно иную форму. Принципу относительности Эйнштейна, как доказывается, удовлетворяет уравнение

, (16)

где 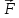– сила, действующая на частицу,– релятивистский импульс. Подставив (14), получим

. (17)

Это и есть основное уравнение релятивистской динамики. Отметим, что сила в теории относительности – величина неинвариантная, в разных системах отсчета ее числовое значение и направление будут различны.

Из уравнения (17) следует неожиданный вывод: вектор ускорения частицы в общем случае не совпадает по направлению с вектором силы.

Доказательство:

, где m(v)-релятивистская масса. Выполнив дифференцирование по времени, получим

Это выражение графически представлено на рис. 5. Таким образом, действительно, вектор ускорения в общем случае не коллинеарен вектору.

Рис. 5