4.4 Относительность одновременности

Предположим, что в системе произошли одновременно события в различных точках (залп ряда орудий), т.е.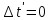;. Тогда используя преобразования Лоренца (6), получим

. (10)

Это значит, что наблюдатель в системе отсчета воспринимает рассматриваемое явление как ряд выстрелов с интервалом, т.е. одновременность событий относительна.

Физическая теория, инвариантная относительно преобразований Лоренца, называется специальной теорией относительности. Формулы и законы, составляющие ее сущность, называются релятивистскими законами (relative – относительный).

5 Релятивистский закон сложения скоростей

Пусть в -системе в плоскостидвижется частица со скоростью, проекции которойи. Найдем с помощью преобразований Лоренца (6) проекцииив-системе. Системадвижется относительно К-системы со скоростью(см. рис.1).

Получим

,

. (11)

При малых скоростях (и) они переходят в закон сложения скоростей классической механики:

,

или векторном виде

.

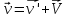Решим обратную задачу.

Найдем с помощью преобразований Лоренца (7) проекции скорости частицы ив-системе, зная ее проекцииив-системе.

Получим

;

(11a)

Отсюда скорость частицы в -системе

.

6 Пространственно-временной интервал

Относительный характер пространственных и временных промежутков отнюдь не означает, что теория относительности вообще отрицает существование каких бы то ни было абсолютных величин, то есть величин, которые не зависели бы от выбора инерциальной системы отсчета.

Инвариантные величины СТО:

1. универсальная скорость распространения взаимодействий, равная скорости света в вакууме «»;

2. интервал между двумя событиями 1 и 2, квадрат которого определяется как

, (12)

где 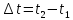– промежуток времени между событиями,– расстояние между двумя точками, в которых происходят данные события ().

В релятивистской механике интервал играет ту же роль, какую в классической механике играет расстояние между двумя точками в трехмерном пространстве. Длина сохраняется при преобразованиях Галилея. Интервал же сохраняется при преобразованиях Лоренца.

В инвариантности интервала легко убедиться, вычислив его непосредственно в - и К-системах отсчета.

Воспользовавшись формулами (7) и учитывая, что и, запишем:

.

Таким образом, . Утверждение «два события разделены таким-то интервалом» имеет абсолютный характер – оно справедливо во всех инерциальных системах отсчета.

Минковский обратил внимание на то, что выражение для интервала можно рассматривать как квадрат расстояния между близкими точками в некотором четырехмерном пространстве с координатами:

В этих координатах

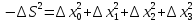. (13)

Четырехмерное пространство, в котором действует формула (13), является псевдоевкливовым и называется миром Минковского. В этом пространстве время является дополнительным измерением, равноправным с обычными пространственными измерениями, а расстояние между двумя четырехмерными точками определяется интервалом.

Задачи

Задача 1. В К -системе отсчета находится неподвижный стержень длины = 1 м, ориентированный под угломк осиOX (рис.) Найти его длину и соответствующий уголв-системе, движущейся относительно-системы со скоростью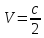вдоль осиOX.

Решение

Длина стрежня в 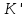-системе

, где .

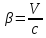Имея в виду, что и, получим

м.

Угол в-системе найдем через тангенс:

Отсюда

Задача 2. Найти расстояние, которое пролетела в К -системе отсчета нестабильная частица от момента ее рождения до распада. Если ее время жизни в этой системе c, а собственное время жизни c.

Решение

1 способ

Найдем скорость частицы из формулы. Получим.

Искомое расстояние равно км.

2 способ решения основан на использовании инвариантности интервала:

,

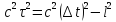где квадрат интервала записан слева в системе отсчета, связанной с самой частицей, а справа – в К -системе отсчета. Отсюда получается тот же результат .

Задача 3. Две ракеты движутся навстречу друг другу со скоростями по отношению к неподвижному наблюдателю. Найти скорость сближения ракет по классической и релятивистской формулам сложения скоростей.

Решение

Рис.

По классической формуле , что противоречит второму постулату теории относительности.

По релятивистской формуле (11а) 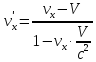найдем скорость частицы 2 в системе отсчета, при этом свяжем с частицей 1-систему отсчета (рис. ).

Подставим в формулу получим

Знак минус означает, что в данном случае частица 2 движется в отрицательном направлении оси 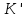-системы отсчета. Следует отметить, что если, то скорость.

Таким образом, мы получили скорость частицы 2 в системе отсчета, связанной с частицей 1 – это и есть скорость сближения частиц. В нашем случае , величина скорости равна.

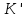Задача 4. Частица движется в К -системе со скоростью под угломк осиX. Найти соответствующий угол в-системе, движущейся со скоростью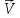, как показано на рис.

Решение

Рис.

В К-системе отсчета

В -системе отсчета с учетом формул (11а) получим

.

После подстановки инайдем

.