
- •Санкт-Петербургский государственный морской технический университет
- •2. Основы теории графов
- •4. Список использованной литературы
- •Задание 3.
- •4. Написать таблицу значений функции. Найти фиктивные переменные для данной функции. Преобразовать данную формулу в эквивалентную ей, но не содержащую фиктивных переменных.
- •1.4. Совершенные дизъюнктивные и конъюнктивные формы булевых функций. Двойственные функции.
- •6. Проверить, являются ли равносильными формулы a и b двумя способами а) составлением таблиц значений; б) приведением формул к сднф или скнф с помощью эквивалентных преобразований
- •1.5. Построение и упрощение формул, задаваемых различными схемами.
- •7. Построить формулы, задаваемые данными схемами. Упростить их. Построить схемы, соответствующие упрощенным формулам.
- •8. Представить функцию в виде дизъюнктивного разложения по переменным, коэффициенты разложения (функции двух переменных) представить соответствующими формулами над множеством связок|,
- •9. С помощью сднф установить, являются ли равносильными следующие днф:
- •1.7. Минимизация булевых функций методом Квайна–Мак-Класки и матричным методом Карно.
- •10. Минимизировать функцию методом Квайна-Мак-Класки и графическим методом Карно. Найти индекс простоты функции.
- •1. Метод Квайна-Мак-Класки.
- •1.8. Представление булевых функций полиномами Жегалкина.
- •11. Представить функцию полиномом Жегалкина.
- •1.9. Проверка принадлежности булевых функций классам Поста. Полные системы булевых функций. Базисы. Задание 12. Проверить, принадлежат ли функции ик классамT0, t1, l, s, m.
- •14. Являются ли полными следующие системы булевых функций Какие из указанных систем образуют базис?
- •1.10. Представление булевых функций в базисе Шеффера и в базисе Вебба .
- •15. Записать функцию в базисе «не и» и в базисе «не или».
- •1.11. Производные булевой функции.
- •16. Найти частные производные булевой функции по каждой переменной и их вес, если .
- •18. Заданы графы g1 и g2. Найти Для графанайти матрицы смежности, инцидентности, достижимости, контрдостижимости, сильных компонент и все маршруты длины 2, исходящие из вершины 1.
- •2.4 Матрицы фундаментальных циклов и матрицы фундаментальных разрезов графа.
- •3.Элементы теории кодирования.
8. Представить функцию в виде дизъюнктивного разложения по переменным, коэффициенты разложения (функции двух переменных) представить соответствующими формулами над множеством связок|,



|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
0 |
| |
|
0 |
0 |
0000 |
1 | |
|
0 |
1 |
0001 |
1 | |
|
1 |
0 |
0010 |
0 | |
|
1 |
1 |
0011 |
0 | |
|
|
|
0 |
|
|
0 |
0 |
0100 |
0 |
|
0 |
1 |
0101 |
1 |
|
1 |
0 |
0110 |
0 |
|
1 |
1 |
0111 |
0 |
|
|
|
1 |
|
|
0 |
0 |
1000 |
0 |
|
0 |
1 |
1001 |
1 |
|
1 |
0 |
1010 |
1 |
|
1 |
1 |
1011 |
1 |
|
|
|
1 |
| |
|
0 |
0 |
1100 |
0 | |
|
0 |
1 |
1101 |
1 | |
|
1 |
0 |
1110 |
1 | |
|
1 |
1 |
1111 |
0 | |
9. С помощью сднф установить, являются ли равносильными следующие днф:




1.7. Минимизация булевых функций методом Квайна–Мак-Класки и матричным методом Карно.
10. Минимизировать функцию методом Квайна-Мак-Класки и графическим методом Карно. Найти индекс простоты функции.
1. Метод Квайна-Мак-Класки.
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
|
№ гр. |
Набор |
№ наб. |
№ склеивания |
Результат склеивания |
№ скл. набора |
Результат склеивания |
Импликанты | |||||
|
0 |
0000 |
0 |
0.1
0.2 0.4 0.8 1.3 2.10 4.12 8.10 8.12 3.11 10.11 10.14 12.14 11.15 14.15 |
000-
00-0 0-00 -000 00-1 -010 0-00 10-0 1-00 -011 101- 1-10 11-0 1-11 111- |
0,2,1,3
0,2,8,10
0,4,8,12 4,12,8,12 8,10,12,14
8,12,10,14
10,11,14,15 10,14,13,15 |
00—
-0-0
--00 --00 1—0
1—0
1-1- 1-1- |
J1
J2
J3
J4
J5
| |||||
|
1 |
0001 0010 0100 1000 |
1 2 4 8 | ||||||||||
|
2 |
0011 1010 1100 |
3 10 12 | ||||||||||
|
3 |
1011 1110 |
11 14 | ||||||||||
|
4 |
1111 |
15 | ||||||||||
|
|
0000 |
0001 |
0010 |
0100 |
1000 |
0011 |
1010 |
1100 |
1011 |
1110 |
1111 |
|
I1 |
+ |
+ |
+ |
|
|
+ |
|
|
|
|
|
|
I2 |
+ |
|
+ |
|
+ |
|
+ |
|
|
|
|
|
I3 |
+ |
|
|
+ |
+ |
|
|
+ |
|
|
|
|
I4 |
|
|
|
|
+ |
|
+ |
+ |
|
+ |
|
|
I5 |
|
|
|
|
|
|
+ |
|
+ |
+ |
+ |
ТДНФ

МДНФ
=
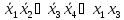
Метод Карно00
01
11
10
00
1
1
1
1
01
1
0
0
0
11
1
0
1
1
10
1
0
1
1
|
0000 |
|
0001 |
|
0011 |
|
0010 00--
|
|
1111 |
|
1110 |
|
1011 |
|
1010 1-1-
|
|
0000 |
|
0100 |
|
1100 |
|
1000 --00
|



























