МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

СЕВМАШВТУЗ

КАФЕДРА №3

Курзанова Е.В.

Сопротивление материалов

Методическое руководство к выполнению лабораторных работ на кручение:

«Испытание цилиндрических образцов из стали и чугуна на кручение до разрушения»

«Определение модуля сдвига при кручении»

Северодвинск

2005

УДК 539.3/8

Курзанова Е.В.

Сопротивление материалов. Методическое руководство к выполнению лабораторных работ на кручение.

Северодвинск. Севмашвтуз, 2005 – 25 стр.

В методическом руководстве к выполнению лабораторных работ на кручение:

«Испытание цилиндрических образцов из стали и чугуна на кручение до разрушения» лабораторная работа № 4 и «Определение модуля сдвига при кручении» лабораторная работа № 5 приводится описание лабораторных работ, выполняемых студентами всех специальностей Севмашвтуза по курсу «Сопротивления материалов».

В методическом руководстве излагаются краткие сведения из теории деформации кручения, содержится описание машины для испытания на кручение КМ-50-1, прибора для измерения углов закручивания.

Методическое руководство содержит методику проведения испытаний, формы отчёта по лабораторным работам и вопросы для защиты лабораторных работ.

Рецензенты:

доцент, канд. технических наук Н. В. Лобанов,

заведующий лабораторией «Сопротивление материалов» В. А. Слуцков,

ведущий инженер НИТИЦ ФГУП «ПО «Севмаш» Ю. П. Голованов

Лицензия на издательскую деятельность код 221, серия ИД №01734 от 11 мая 2000 г.

ISBN © СЕВМАШВТУЗ, 2004

СОДЕРЖАНИЕ

Предисловие …………………………………………………………….4

Основные понятия темы Кручение……………………………………..5

1. Испытательные машины и измерительные приборы…………..11

1. Машина для испытания на кручение КМ-50-1……………..……11

2. Прибор для измерения углов закручивания (прибор Бояршинова)……………………………….……………………….13

2. Описание лабораторных работ………………………………………15

2.1. Испытание цилиндрических образцов из стали и чугуна

на кручение до разрушения (лабораторная работа № 4)……………….15

2.2. Определение модуля сдвига при кручение (лабораторная

работа № 5)………………………………………………………………..22

Список литературы……………………………………………………….26

ПРЕДИСЛОВИЕ

Методическое руководство к выполнению лабораторных работ по кручению содержит основные теоретические понятия раздела Кручение курса Сопротивление материалов.

В методическом руководстве содержится описание и схемы испытательной машины и измерительного прибора, методика проведения испытаний, формы выполнения отчётов по лабораторной работе № 4 «Испытание цилиндрических образцов из чугуна и стали на кручение до разрушения» и лабораторной работе №5 «Определение модуля сдвига при кручении», проверочные вопросы для защиты лабораторных работ.

Целью методического руководства является оказание помощи студентам при выполнении лабораторных работ по разделу Кручение, при оформлении отчета и защиты лабораторных работ.

Методическое руководство предназначено для студентов всех специальностей, изучающих курс «Сопротивление материалов».

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ.

Тема: Кручение стержней круглого поперечного сечения.

Основные понятия и зависимости.

Под кручением стержня понимается такой вид нагружения, при котором в его поперечных сечениях возникает только один внутренний силовой фактор - крутящий момент М_кр, а в поперечных сечениях возникают только касательные напряжения τ.

Валом называется стержень, работающий на кручение.

Гипотезы, принятые при кручении:

1. Выбранное в стержне до нагружения поперечное сечение остается плоским и перпендикулярным оси и после нагружения. Радиусы поперечных сечений не искривляются.

2. Расстояния между поперечными сечениями не изменяются, так как отсутствуют нормальные напряжения и линейные деформации равны нулю.

3. Сечения поворачиваются друг относительно друга на угол закручивания dφ на элементарном расстоянии между сечениями dх. Чем больше расстояние между сечениями, тем больше угол закручивания. Полный угол закручивания - φ –характеризует поворот концевого сечения относительно другого неподвижного на расстоянии, равном длине вала -L. Чтобы исключить влияние длины вала вводится понятие относительного (погонного) угла закручивания -.

=φ/L=dφ/dx – отношение угла закручивания к расстоянию между сечениями. Имеет размерность см^-1.

Если на поверхность вала (см. рис. 1) с одним защемлённым концом, а другим свободным, нанести сетку, состоящую из линий, параллельных оси, и линий, представляющих собой параллельные круги и приложить к свободному концу вала нагрузку в виде скручивающего момента М_кр, то первоначально прямые углы сетки будут искажаться, перекашиваться (это особенно наглядно, если в качестве материала взять резину). Угол γ называется угловой деформацией или углом сдвига. Установлено, что в пределах упругих деформаций касательные напряжения τ и угол сдвига γ связаны между собой линейной зависимостью:

τ=G∙γ закон Гука при сдвиге, (1)

Рис. 1

G – коэффициент пропорциональности называется модулем сдвига, или модулем упругости второго рода и характеризует жесткость материала при сдвиге. Имеет размерность: кГ/см² или кГ/мм², или Н/мм²(МПа-мегапаскаль)

Для одного и того же материала между модулем упругости первого рода - Е (модуль Юнга), модулем упругости второго рода - G (модуль сдвига) и коэффициентом Пуассона - μ = ε^,/ε (отношение относительной поперечной деформации: к относительной продольной:) существует следующая зависимость:

(2)

При кручении вал рассчитывают на прочность и жёсткость.

Условие прочности при кручении имеет вид:

τ _max ≤ [τ]. (3)

При расчётах на прочность находят максимальные касательные напряжения τ_max, которые действуют на поверхности вала и сравнивают их с допускаемыми [τ]:

τ _max ≤ [τ].

τ _max = , (4)

где: М_кр – крутящий момент в сечении, берётся с эпюры крутящих моментов;

W_ρ = I_ρ/ρ_max – полярный момент сопротивления сечения.

Так как I_ρ = – полярный момент инерции сечения; ρ_max=d/2, то W_ρ=

Для нахождения касательного напряжения τ_ρ в любой точке поперечного сечения вала, находящийся на расстоянии ρ от центра (см. рис.2) справедлива следующая формула:

τ_ρ = (5)

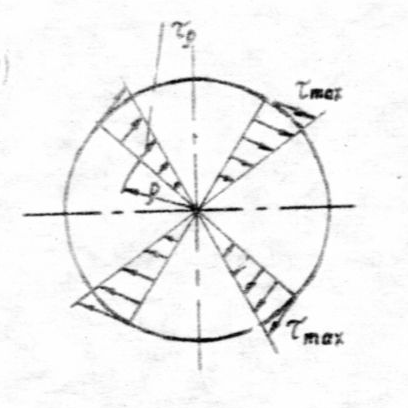
Рис. 2

Условие жесткости при кручении имеет вид:, где [] –допускаемый угол имеет размерность рад/м в данной формуле.

При расчетах на жесткость находят максимальный относительный угол закручивания: (6)

и сравнивают его с допускаемым []:

(7)

Чтобы перейти к размерности град/м условие жесткости должно иметь следующий вид:

, (8)

где [] - относительный угол закручивания имеет размерность град/м, величина лежит в пределах от 0,25 град/м до 1 град/м и зависит от назначения вала.

Величина-G I_ρ (произведение модуля упругости второго рода G на полярный момент инерции площади поперечного сечения I_ρ)- называется жесткостью сечения вала при кручении и показывает влияние материала и геометрического размера сечения вала на получаемую деформацию.

Угол закручивания круглого стержня в пределах упругих деформаций рассчитывают по следующей формуле:

(9)

где М_кр - крутящий момент,

ℓ - длина вала,

G - модуль сдвига

I_ρ - полярный момент инерции площади поперечного сечения сплошного стержня диаметром d,

- полярный момент инерции трубчатого стержня с внутренним диаметром и наружным диаметром ,

G - жесткость сечения стержня при кручении, кГ

Чтобы получить формулу (5) для определения касательного напряжения τ в любой точке сечения стержня и формулу (6) для определения относительного угла закручивания круглого стержня , необходимо рассмотреть некоторый участок вала длиной (см. рис. 3).

Рис. 3

Вал подвержен действию некоторого скручивающего момента М_к, вызывающего внутренний крутящий момент М_кр

Пусть угол поворота одного из сечений m-m выделенного элемента вала будет, тогда угол поворота другого сечения n-n элементарного участка будет , т. е. угол закручивания участка стержня длиной будет . Следовательно, если до деформации радиус сечения m-m и радиус сечения n-n находились в одной диаметральной плоскости, то после деформации кручения радиус займёт положение, составляющее угол

с его положением до деформации. Образующая после деформации займёт некоторое новое положение под углом к её первоначальному положению .

Угол между образующими и представляет cобой не что иное как относительный сдвиг, или угол сдвига:

tg.

Учитывая, что =, а =, угол сдвига можно представить в виде

(10)

Величина , как уже известно (см. пункт 3 основных гипотез, принятых при кручении), является относительным (погонным) углом закручивания и обозначается через . Учитывая это формулу (10) можно записать так:

. (11)

Теперь рассмотрим физическую сторону задачи, устанавливающую связь между напряжением и деформацией. Поскольку элемент испытывает чистый сдвиг, то, учитывая выражение (10) согласно формуле (1) получим:

. (12)

Так как при закручивании поперечные сечения вала остаются плоскими, а радиусы прямыми (см. пункт 1 гипотез, принятых при кручении), то выражения для угла сдвига и касательного напряжения в сечении на расстоянии от центра его можно представить формулами, аналогичными формулам (10) и (11):

;

. (13)

Формулы (13) показывают, что касательные напряжения в поперечном сечении изменяются по линейному закону прямо пропорционально расстоянию точек от центра сечения (см. рис. 2). Очевидно, максимальные напряжения будут у поверхности стержня, при . Таким образом, выражение (12) можно переписать в виде:

.

Так как М_кр будет единственным усилием в сечении вала, представляющим собой суммарный момент от касательных напряжений, действующих в плоскости поперечного сечения:

(14)

Подставляя выражение (13) для касательного напряжения в уравнение (14), будем иметь:

.

Отсюда получим формулу для определения относительного угла закручивания круглого стержня (см. формулу (6), указанную ранее):

(15)

Зная выражение (15) относительного угла закручивания, можно записать формулу для определения взаимного угла закручивания двух сечений, расположенных на расстоянии :

.

Если в пределах цилиндрического участка стержня длиною крутящие моменты в сечениях не изменяются, то

(16)

Формулу (16), устанавливающую связь между силовым фактором при кручении (М_кр) и соответствующей деформацией кручения (углом ), часто называют законом Гука при кручении.

Для определения касательного напряжения в любой точке сечения стержня достаточно в формулу (13) подставить выражение для по формуле (15). Тогда:

(17)

Формула (17) аналогична формуле (5), что и требовалось доказать.