7. Гамма-распределение

Для описания случайной величины, ограниченной с одной стороны, используется гамма-распределение, плотность вероятности которого равна

где параметры.- Гамма-функция.

Функция распределения имеет вид

Построим графики плотности вероятности для значений параметров ,,

и для значений параметров ,

При фиксированном иплотность вероятности гамма-распределения представляет собой убывающую функцию, а приодновершинную кривую с максимумом в точке.

При больших значениях гамма-распределение можно аппроксимировать нормальным распределением

,

где - функция распределения нормированного нормального закона.

При из гамма-распределения получается показательное распределение, плотность которого равна

Гамма-распределение позволяет описывать самые различные случайные величины со значениями от 0 до . Особенно часто оно используется в теории надежности в качестве модели времени безотказной работы различных приборов и сложных систем.

Частным случаем гамма–распределения при являетсяраспределение Эрланга, которое встречается в задачах резервирования теории надежности. Пусть имеется несколько резервных элементов, которые по мере возникновения отказов последовательно подключаются на место основного и выполняют его функции. Совокупность основного и резервного элементов называется резервной группой. Плотность распределения времени безотказной работы элементов задается формулой

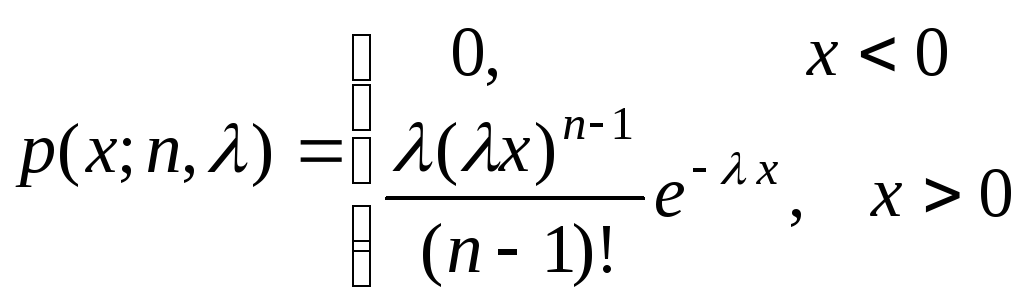
Распределение Эрланга имеет сумма независимых случайных величин, каждая из которых имеет показательное распределение с параметром.

8. Распределение .

Частным случаем гамма–распределения с параметрами является распределение с степенями свободы. .

Это распределение описывает случайную величину , где– независимые случайные величины, одинаково распределенные по нормальному закону с параметрами.

На рис. приведены графики плотности распределения для значений параметра .

9. Распределение Стьюдента (распределение).

Распределением Стьюдента (илираспределением) с степенями свободы называется распределение случайной величины

, где – независимые случайные величины, одинаково распределенные по нормальному закону с параметрами.

Плотность вероятности такого распределения имеет вид

. .

При график плотности вероятности распределения Стьюдента приближается к графику нормального распределения.

На рис. представлены графики плотности распределения Стьюдента в случае . Эти графики симметричны относительно оси ординат.

При распределение Стьюдента совпадает с распределением Коши

, для которого функция распределения имеет вид

.

63