3. Распределение Релея.

По закону Релея распределены амплитуды волн, огибающая случайных шумов.

Плотность вероятности распределения Релея имеет вид

Интегрируя это выражение, найдем функцию распределения

Построим графики плотности вероятности и функции распределения для значений (сплошной линией) и(пунктирной линией

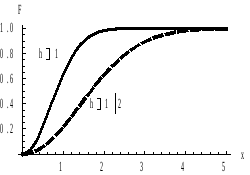
Плотность вероятности Функция распределения

Плотность вероятности имеет максимум в точке .

4. Показательное распределение

Плотность вероятности и функция распределения для показательного распределения имеют вид

Построим графики плотности вероятности и функции распределения для значений (сплошной линией) и(пунктирной линией)

Плотность вероятности Функция распределения

Среди непрерывных распределений только показательное распределение обладает свойством отсутствия последействия.

Действительно, пусть элемент, время безотказной работы которого распределено по показательному закону, проработал время. Тогда для вероятности времени безотказной работы.

Действительно,

Распределение остатка времени безотказной работы не зависит от того, сколько времени прибор проработал. Предварительное использование элемента не влияет на оставшееся время его работы, т.е. у элемента нет старения. Показательное распределение используется в качестве модели времени безотказной работы сложной системы, элементы которой восстанавливаются в процессе работы..

По показательному закону распределена длительность работы многих приборов. Вероятность отказа прибора за время равнавероятность безотказной работы прибора за время называется функцией надежности.

5. Закон Вейбулла.

Обобщением показательного распределения и распределения Релея является распределение Вейбулла, для которого плотность вероятности и функция распределения имеют следующее представление.

где ,

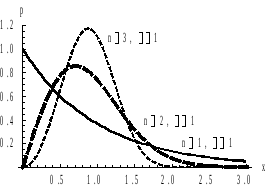
Плотность вероятности Функция распределения

При закон Вейбулла становится показательным распределением, а при– распределением Релея. На рис приведены графики плотности вероятности и функции распределения в случаедля(сплошной линией), для(пунктирной линией с длинными штрихами ), для(пунктирной линией с короткими штрихами ).

6. Распределение Коши.

Пусть построена окружность единичного радиуса с центром в начале координат. На окружности наугад выбирают точку, например, . В этой точке проводят касательную к окружности и вычисляют длинуотрезка касательной до пересечения с осью. Найдем функцию распределения длин отрезков таких касательных. Построим точки,,на окружности, для которых длины отрезков касательных будут равны. Тогда событиепроизойдет тогда, когда точка будет выбрана на одной из дугили. Вероятность

.

Следовательно, функция распределения

.

Плотность вероятности такого распределения равна

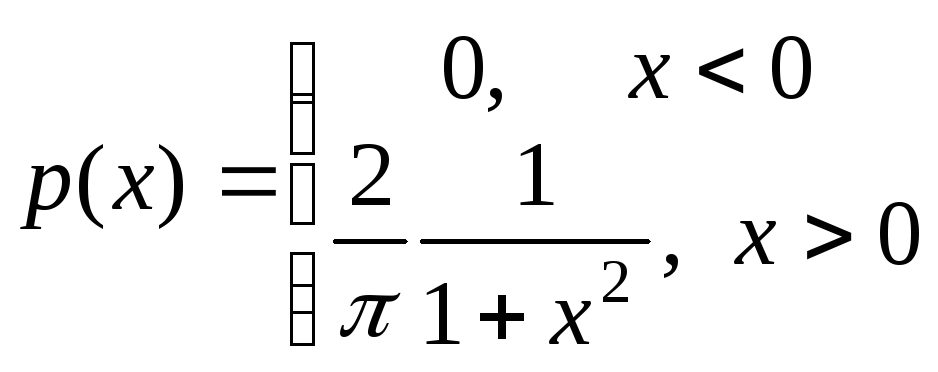
Распределение с такой функцией называется распределением Коши. Распределением Коши называется также распределение с плотностью и функцией распределения

. ,

На рис. представлены графики плотности вероятности и функции распределения для случайной величины, распределенной по закону Коши.