
Л8_ Теория вероятностей
.docЛекция 8.
Кратные интегралы.
Мера Жордана. Жордановы множества.
Областью
![]() в пространстве
в пространстве
![]() называется непустое связное открытое
множество. Замыкание
называется непустое связное открытое
множество. Замыкание
![]() области
области
![]() называется замкнутой областью. Замкнутым
называется множество, содержащее все
свои предельные точки. Замкнутое
множество
называется замкнутой областью. Замкнутым
называется множество, содержащее все
свои предельные точки. Замкнутое
множество
![]() называется границей области
называется границей области
![]() .
.
Диаметром
области
![]() называется
точная верхняя грань расстояний между
точками области
называется
точная верхняя грань расстояний между
точками области
 ,
где
,
где
![]() ,
,
![]() ,
,![]()
![]() .
.
Для замкнутой ограниченной области диаметр равен наибольшему из расстояний между точками области.
Стандартным прямоугольником называется прямоугольник со сторонами, параллельными координатным осям, например,
замкнутый стандартный прямоугольник
![]() (1)
(1)
открытый стандартный прямоугольник
![]() ,
(2)
,
(2)
а
также полуоткрытые прямоугольники, для
которых хотя бы одно из трех неравенств
в вышеприведенном определении (1) является
строгим. Обозначим через
![]() множество стандартных прямоугольников
на плоскости.
множество стандартных прямоугольников
на плоскости.
Два
прямоугольника
![]() ,
,
![]() называются непересекающимися, если они
не имеют общих внутренних точек. Для
прямоугольника
называются непересекающимися, если они
не имеют общих внутренних точек. Для
прямоугольника
![]() ,
который является объединением
,
который является объединением
![]() непересекающихся стандартных
прямоугольников
непересекающихся стандартных
прямоугольников
![]() ,
будем использовать специальное
обозначение
,
будем использовать специальное
обозначение
![]() .
Каждому прямоугольнику
.
Каждому прямоугольнику
![]() можно сопоставить число
можно сопоставить число
![]() – его меру, которая удовлетворяет
условиям неотрицательности:
– его меру, которая удовлетворяет
условиям неотрицательности:
![]() и аддитивности:
и аддитивности:
![]() .
В частности, мерой непустого стандартного
прямоугольника
.
В частности, мерой непустого стандартного
прямоугольника
![]() (замкнутого, открытого или полуоткрытого),
определяемого числами
(замкнутого, открытого или полуоткрытого),
определяемого числами
![]() ,
является его площадь
,
является его площадь
![]() .
.
Связное
плоское множество
![]() называется элементарным, если его можно
представить как объединение конечного
числа непересекающихся стандартных
прямоугольников
называется элементарным, если его можно
представить как объединение конечного
числа непересекающихся стандартных
прямоугольников
![]() .
.
Стандартным
прямоугольным параллелепипедом в
![]() называется
называется
![]() .
Два параллелепипеда
.
Два параллелепипеда
![]() ,
,
![]() называются непересекающимися, если они
не имеют общих внутренних точек. Мерой
или объемом стандартного параллелепипеда
называются непересекающимися, если они
не имеют общих внутренних точек. Мерой
или объемом стандартного параллелепипеда
![]() называется
называется
![]()
![]() .
.
Элементарным
телом называется связное множество
точек пространства
![]() ,
представляющее собой объединение
конечного числа непересекающихся
,
представляющее собой объединение
конечного числа непересекающихся
![]() -мерных
стандартных прямоугольных параллелепипедов.
Мера или объем элементарного тела
-мерных
стандартных прямоугольных параллелепипедов.
Мера или объем элементарного тела
![]() равна сумме мер стандартных прямоугольных
параллелепипедов
равна сумме мер стандартных прямоугольных
параллелепипедов
![]() .
.
Рассмотрим
произвольную область
![]() на плоскости, проведем прямые, параллельные
координатным осям. В результате получим
стандартные прямоугольники. Обозначим
такое разбиение через
на плоскости, проведем прямые, параллельные
координатным осям. В результате получим
стандартные прямоугольники. Обозначим
такое разбиение через
![]() .
Пусть
.
Пусть
![]() – площадь стандартных прямоугольников,
лежащих внутри
– площадь стандартных прямоугольников,
лежащих внутри
![]() и не имеющих общих точек с границей
и не имеющих общих точек с границей
![]() области, а
области, а
![]() – площадь стандартных прямоугольников,
имеющих хотя бы одну общую точку с
границей
– площадь стандартных прямоугольников,
имеющих хотя бы одну общую точку с
границей
![]() области. Тогда для разных разбиений
области. Тогда для разных разбиений
![]() получим множества
получим множества![]() и
и
![]() .
.
Нижней
или внутренней мерой Жордана множества
![]() называется
называется
![]() ;
верхней или внешней мерой Жордана
называется
;
верхней или внешней мерой Жордана
называется
![]()
![]() .
Множество
.
Множество![]() называется измеримым
по Жордану,
если
называется измеримым
по Жордану,
если
![]() и
и
![]() конечны и
конечны и
![]() .
В этом случае величина
.
В этом случае величина
![]() называется мерой
Жордана,
а множество
называется мерой
Жордана,
а множество
![]() называется жордановым.
Аналогичным образом определяется мера
области
называется жордановым.
Аналогичным образом определяется мера
области
![]() ,
,
![]() .
Мера Жордана обладает свойствами
неотрицательности
.
Мера Жордана обладает свойствами
неотрицательности
![]() (
(![]() ),
аддитивности (
),
аддитивности (![]() )
и монотонности (
)
и монотонности (![]()
![]() .
.![]() Если
Если
![]() жорданово множество, то
жорданово множество, то
![]() .
.
Множество
![]()
![]() ,
границей которого является спрямляемая
(в частности кусочно-гладкая) замкнутая
кривая без самопересечений является
жордановым множеством. Множество
,
границей которого является спрямляемая
(в частности кусочно-гладкая) замкнутая
кривая без самопересечений является
жордановым множеством. Множество
![]() ,
границей которого является кусочно-гладкая
замкнутая поверхность без самопересечений,
является жордановым множеством.
,
границей которого является кусочно-гладкая
замкнутая поверхность без самопересечений,
является жордановым множеством.
Жордановой мерой ограниченного участка кривой или отрезка является длина, жордановой мерой ограниченной замкнутой плоской области или поверхности является площадь, жордановой мерой тела в трехмерном пространстве, ограниченного замкнутой поверхностью, является объем.
Интеграл Римана по измеримому по Жордану множеству и его свойства
Пусть
![]() – жорданово множество, на котором
задана ограниченная функция
– жорданово множество, на котором
задана ограниченная функция
![]() .
Разбиением множества
.
Разбиением множества
![]() называется конечная система непустых
непересекающихся жордановых множеств
называется конечная система непустых
непересекающихся жордановых множеств
![]() ,
объединение которых равно заданному
множеству:
,
объединение которых равно заданному
множеству:
![]() .
Диаметром разбиения
.
Диаметром разбиения
![]() называется
называется
![]() .
Выберем произвольно точки
.
Выберем произвольно точки
![]() ,
,
![]() и составим интегральную сумму Римана
и составим интегральную сумму Римана
![]() (3)
(3)
Интегралом
Римана от функции
![]() по измеримому по Жордану множеству
по измеримому по Жордану множеству
![]() называется число
называется число
![]() ,
(4)
,
(4)
которое
не зависит ни от способа разбиения
множества
![]() ,
ни от выбора точек
,
ни от выбора точек
![]() .
Для интеграла Римана используется также
следующее обозначение
.
Для интеграла Римана используется также
следующее обозначение
![]() .
.
Такой интеграл называется кратным интегралом.
Если
![]() – плоская область, жордановой мерой
которой является площадь, то
– плоская область, жордановой мерой
которой является площадь, то
![]() =
=![]() – двойной интеграл. Если
– двойной интеграл. Если
![]() – область в трехмерном пространстве,
жордановой мерой которой является
объем, то
– область в трехмерном пространстве,
жордановой мерой которой является
объем, то
![]() =
=![]() – тройной интеграл.
– тройной интеграл.
Множество
интегрируемых по Риману функций на
множестве
![]() обозначается R
обозначается R![]() .
.
Если
![]() R
R![]() и
и
![]() ,
то
,
то
![]() ограничена на
ограничена на
![]() .
.
Если
![]() измеримое по Жордану замкнутое
ограниченное множество и
измеримое по Жордану замкнутое
ограниченное множество и
![]() ,
то
,
то
![]() R
R![]() .
.
Если
![]() измеримое по Жордану замкнутое
ограниченное множество,
измеримое по Жордану замкнутое
ограниченное множество,
![]() ограничена на
ограничена на
![]() и множество точек разрыва функции имеет
жорданову меру нуль, то
и множество точек разрыва функции имеет
жорданову меру нуль, то
![]() R
R![]() .
В
частности, ограниченная функция, имеющая
не более чем счетное множество точек
разрыва на жордановом множестве
.
В
частности, ограниченная функция, имеющая
не более чем счетное множество точек
разрыва на жордановом множестве
![]() ,
интегрируема по Риману на этом множестве.
,
интегрируема по Риману на этом множестве.
Основные свойства кратного интеграла Римана
Будем
считать в дальнейшем множества
![]() измеримыми
по Жордану и функции
измеримыми
по Жордану и функции
![]() ограниченными
на рассматриваемых множествах.
ограниченными
на рассматриваемых множествах.
1.
![]() .
.
2.
![]() R
R![]() ,
,
![]() R
R![]()
![]()
![]()
![]() R
R![]() для
для
![]() любых
постоянных
любых
постоянных
![]() и
и
![]() и
и
![]() (свойство линейности интеграла).
(свойство линейности интеграла).
3.
![]() R
R![]() ,
,
![]() R
R![]() ,
,
![]()
![]()
![]()
![]() R
R![]() и
и
![]() (свойство аддитивности интеграла).
Отметим, что здесь существенным условием
является ограниченность функции на
множествах
(свойство аддитивности интеграла).
Отметим, что здесь существенным условием
является ограниченность функции на
множествах
![]() и
и
![]() .
.
4.
![]() R
R![]() ,
,
![]() R
R![]()
![]()
![]()
![]() R
R![]() и
и
 R
R![]() ,
если
,
если
![]() .
.
5.
Если
![]() R
R![]() ,
,
![]() R
R![]() и
и
![]() для
любых
для
любых
![]() ,
то
,
то
![]() .
В частности, если
.
В частности, если
![]() R
R![]() и
и
![]() для любых
для любых
![]() ,
то
,
то
![]() .
.
6.
Если
![]() R
R![]() ,
,
![]() ,
,
![]() ,
то
,
то
![]() .
.
7.
Если
![]() R
R![]() ,
,
![]() ,
,
![]() ,
,
![]() R
R![]() ,
,
![]() для любых
для любых
![]() ,
то
,
то
![]() .
.
8.
Если
![]() ограничена на
ограничена на
![]() ,
,
![]() R
R![]() и
и
![]() почти везде на
почти везде на
![]() (т.е. равенство нарушается на множестве
меры нуль), то
(т.е. равенство нарушается на множестве
меры нуль), то
![]() .
.
Сведение кратных интегралов к повторным интегралам
Для вычисления двойных и тройных интегралов необходимо свести их к повторным интегралам. Это можно сделать на основе теоремы Фубини.
Область
![]() ,
где
,
где
![]() ,
,
![]() ,
называется стандартной относительно
оси
,
называется стандартной относительно
оси
![]() ,
если любая прямая, параллельная оси
,
если любая прямая, параллельная оси
![]() ,
пересекает границу этой области не
более, чем в двух точках. Иногда такая
область называется правильной в
направлении оси
,
пересекает границу этой области не
более, чем в двух точках. Иногда такая
область называется правильной в
направлении оси
![]() .
Аналогично определяются область на
плоскости, стандартная относительно
оси
.
Аналогично определяются область на
плоскости, стандартная относительно
оси
![]() (правильная
в направлении оси
(правильная
в направлении оси
![]() ):
):
![]() ,
где
,
где
![]() ,
,
![]() .
Стандартная относительно координатной
оси область и ее замыкание являются
жордановыми множествами.
.
Стандартная относительно координатной
оси область и ее замыкание являются
жордановыми множествами.
Теорема Фубини для стандартной плоской области.
Если
![]() ,
где,
,
где,
![]() ,
,
![]() и
и
![]() ,
то
,
то
 .
.
![]() (5)
(5)
Если
![]() ,
где
,
где
![]() ,
,
![]() и
и
![]() ,
то
,
то
 .
(6)
.
(6)
Замечание.
При практическом использовании формул
необходимо, чтобы
![]() ,
,
![]() (соответственно
(соответственно
![]() ,
,
![]() ),
в противном случае представляют интеграл
в виде суммы интегралов.
),
в противном случае представляют интеграл
в виде суммы интегралов.
Теорема Фубини для правильной пространственной области.
Пусть
![]() ограниченная и замкнутая пространственная
область, правильная в направлении оси
ограниченная и замкнутая пространственная
область, правильная в направлении оси
![]() ,
т.е. любая прямая, параллельная оси,
пересекает границу области не более
чем в двух точках. Тогда
,
т.е. любая прямая, параллельная оси,
пересекает границу области не более
чем в двух точках. Тогда
![]() – измеримый компакт. Если
– измеримый компакт. Если

![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
то
,
то
 .
(7)
.
(7)
Аналогично
формулируется теорема Фубини для
пространственной области, правильной
в направлении оси
![]() :
если
:
если
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
то
,
то
 .
(8)
.
(8)
Теорема
Фубини для пространственной области,
правильной в направлении оси
![]() :
если
:
если
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
то
,
то
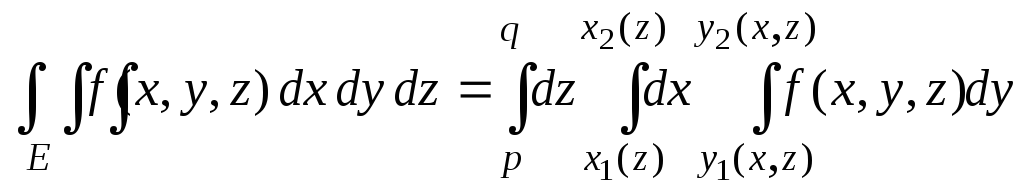 .
(9)
.
(9)
Теорема
Фубини для правильной области в
![]() .
.
Пусть
![]() – измеримый по Жордану компакт в
– измеримый по Жордану компакт в
![]() .
.
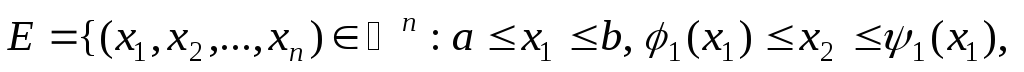 …,
…,
![]() .
Функции
.
Функции
![]() ,
…,
,
…,![]() ,
,
![]() непрерывны в области определения
(например, функции
непрерывны в области определения
(например, функции
![]() ,
,
![]() непрерывны на
непрерывны на
![]() – измеримом по Жордану компакте), функция
– измеримом по Жордану компакте), функция
![]() .
Тогда
.
Тогда
 (10)
(10)
Пример
1
. Вычислить интеграл
![]() ,
где
,
где
![]() –
область, ограниченная прямыми
–
область, ограниченная прямыми
![]() ,
,
![]() и гиперболой
и гиперболой
![]() .
.

Найдем точки пересечения кривых, ограничивающих заданную область, решив соответствующие системы уравнений
![]() .
.
![]()
![]()
![]()
Отсюда
следует, что область
![]() может быть представлена в виде
может быть представлена в виде
![]() .
Тогда интеграл
.
Тогда интеграл
![]() равен
равен

Область
![]() можно представить также в виде
можно представить также в виде
![]() ,
где
,
где
![]() ,
,
![]()
.и
тогда интеграл
![]() представляет собой сумму двух интегралов
представляет собой сумму двух интегралов
![]()
Пример
2.
Вычислить тройным интегрированием
объем тела
![]() ,
ограниченного цилиндрами
,
ограниченного цилиндрами
![]() ,
,
![]() и плоскостями
и плоскостями
![]() ,
,
![]() .
.
Объем
тела определяется тройным интегралом
![]() .
Сведем тройной интеграл к трехкратному.
.
Сведем тройной интеграл к трехкратному.

Здесь видны две цилиндрические поверхности, которые ограничивают тело снизу и сверху и две плоскости. Построим тело, объем которого нужно найти.

Спроектируем
тело на плоскость
![]() .
В результате получится прямоугольник,
две стороны которого лежат на прямых с
уравнениями
.
В результате получится прямоугольник,
две стороны которого лежат на прямых с
уравнениями
![]() ,
,
![]() .
Найдем уравнения прямых, на которых
лежат две другие стороны прямоугольника.
Для этого исключим из уравнений цилиндров
переменную
.
Найдем уравнения прямых, на которых
лежат две другие стороны прямоугольника.
Для этого исключим из уравнений цилиндров
переменную
![]() и решим полученное уравнение
и решим полученное уравнение
