модуль 1

и с^-1, а = 4,4 с^-1, т.е.

здесь действительно

Добротность в данном случае

= 130

Задача 4 Показать, что при малом затухании отношение амплитуды колебаний при резонансной частоте к амплитуде при очень малых частотах равно добротности осциллятора.

Решение

При амплитуда

, равна

.

При .

Из отношения

.

Видно, что для систем с малым затуханием добротность может быть очень большой.

Тесты

1. При уменьшении добротности колебательной системы его резонансная характеристика становится:

1. – более острой; 2. – более широкой и пологой; 3. – несимметричной относительно резонансной частоты; 4. – правый край резонансной характеристики увеличивает амплитуду; 5. – остается без изменений.

2. Собственная частота осциллятора 1 в два раза больше частоты осциллятора 2. Чему равно отношение добротностей Q₁/Q₂, если колебания совершаются в одной и той же среде?

1. – 1; 2. – 2; 3. – 0,5; 4. – 4; 5. – 0,25.

3. Уравнение движения пружинного маятника является дифференциальным уравнением…

1. – свободных затухающих колебаний; 2. – свободных незатухающих колебаний; 3. – вынужденных колебаний; 4. – не является уравнением колебаний; 5. – это уравнение стоячей волны в стержне.

4. На рисунке представлена зависимость амплитуды колебаний математического маятника от частоты внешней силы. Длина нити равна:

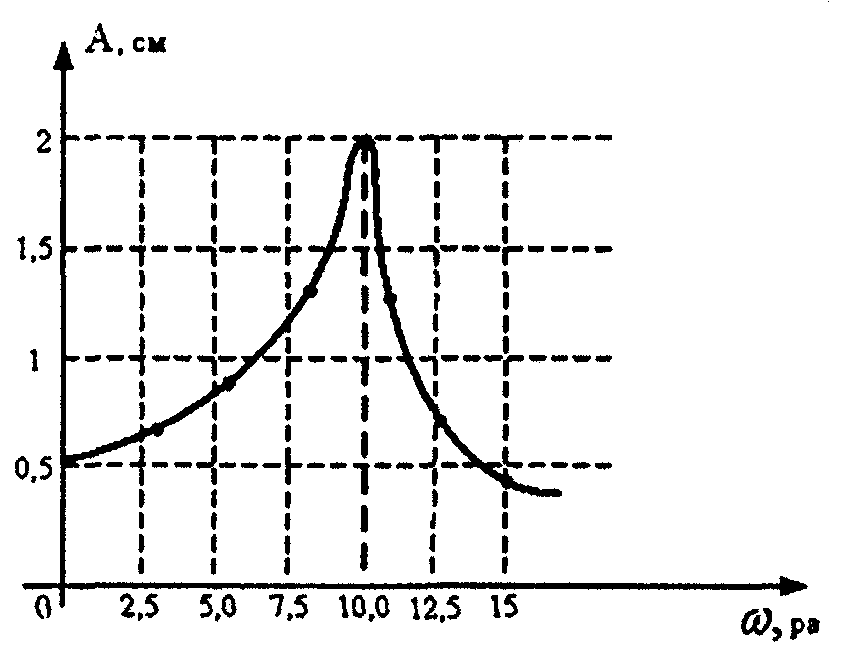
1.– 0,1 м; 2. – 0,02 м; 3. – 0,2 м; 4. – 1 м.

5. Единицей добротности колебательной системы является….

1. – метр; 2. – секунда; 3. – секунда в минус первой степени; 4. – метр в минус первой степени; 5. – величина безразмерна.

6. В каком случае возникает резонанс в системе с малым затуханием (высокой добротностью)?

1– Собственная частота колебаний равна нулю; 2. – Частота вынуждающей силы близка к нулю; 3. – Фаза вынуждающей силы совпадает с фазой колебаний; 4. – Частота вынуждающей силы близка к собственной частоте; 5. – Отношение частоты вынуждающей силы к собственной частоте равно добротности.

7. При увеличении добротности колебательной системы его резонансная характеристика становится:

1. – более острой; 2. – более широкой и пологой; 3. – несимметричной относительно резонансной частоты; 4. – правый край резонансной характеристики увеличивает амплитуду; 5. – остается без изменений.

8. В каком случае возникает резонанс в системе с малым затуханием (высокой добротностью)?

1. – Собственная частота колебаний равна нулю; 2. – Частота вынуждающей силы близка к нулю; 3. – Фаза вынуждающей силы совпадает с фазой колебаний; 4. – Частота вынуждающей силы близка к собственной частоте; 5. – Отношение частоты вынуждающей силы к собственной частоте равно добротности.

9. На рисунке изображен график затухающих колебаний, где S – колеблющаяся величина, описываемая уравнением . Определите время релаксации (в с).

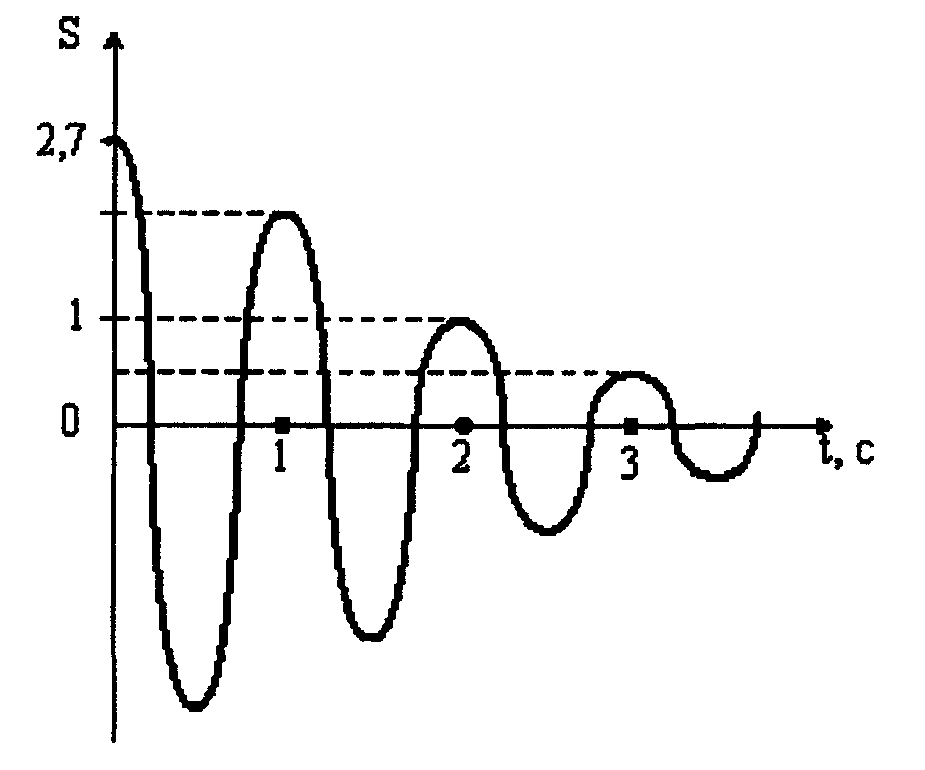
1.– 0,5; 2. – 3; 3. – 2; 4. – 1.

10. Уравнение движения пружинного маятника является дифференциальным уравнением…

1.– свободных незатухающих колебаний; 2. – апериодического движения; 3. – вынужденных колебаний; 4. – свободных затухающих колебаний.

11. В каком виде колебаний наблюдается явление резонанса и при каких условиях?

1. – Резонанс можно наблюдать при вынужденных колебаниях при совпадении собственной частоты колебаний в системе с частотой периодически изменяющейся внешней силы; 2. – Вынужденные колебания, при увеличении амплитуды колебаний периодически действующей внешней силы; 3 – Свободные колебания, при совпадении их частоты с частотой свободных колебаний в другой системе; 4. – Свободные колебания, при совпадении их частоты с собственной частотой колебаний системы; 5. – Резонанс можно наблюдать при вынужденных колебаниях, при совпадении собственной частоты колебаний в системе с частотой периодически изменяющейся внешней силы, фаза внешней силы должна обеспечивать компенсацию потерь энергии за период.

12. Амплитуда колебаний осциллятора А убывает в 2 раза за 1 с, а осциллятора В – за 2 с. Отношение коэффициентов затухания равно:

1. – 0,5; 2. – 2; 3. – 4; 4. – Зависит от соотношения амплитуд; 5. – Зависит от соотношения частот.

13. Уравнение движения пружинного маятника является дифференциальным уравнением…

1. – свободных затухающих колебаний; 2. – свободных незатухающих колебаний; 3. – ангармонических колебаний; 4. – вынужденных колебаний.

14. Амплитуда затухающих колебаний убывает по закону , где …

1. – частота затухающих колебаний; 2. – коэффициент затухания; 3. – логарифмический декремент затухания; 4. – декремент затухания; 5. – добротность колебательной системы.

15. Если коэффициент затухания колебательной системы превышает собственную частоту колебаний, то колебания становятся:

1. – синусоидальными; 2. – вынужденными; 3. – апериодическими; 4. – хаотическими; 5. – появляются биения.

16. При увеличении коэффициента затухания период свободных колебаний:

1. – возрастает; 2. – убывает; 3. – не изменяется; 4. – колеблется вокруг прежнего значения; 5. – изменяется произвольно.

17. Относительная убыль энергии за период колебаний при слабом затухании равна:

1. – ; 2. – ; 3. – ; 4. – ; 5. – , где – коэффициент затухания; – логарифмический декремент затухания.

18. Коэффициент затухания вычисляется по формуле:

1. – ; 2. – ; 3. – ; 4. – ; 5. – .

19. Механическую систему, совершавшую незатухающие колебания, поместили в среду, обладающую незначительным трением. Амплитуда колебаний будет с течением времени…

1. – оставаться неизменной; 2. – увеличиваться по линейному закону; 3. – увеличиваться по экспоненциальному закону; 4. – уменьшаться по экспоненциальному закону; 5. – уменьшаться по линейному закону.

20. Логарифмический декремент затухания , коэффициент затухания и период колебаний связаны соотношением:

1. – ; 2. – ; 3. ; 4. – ; 5. – .

21. Частота вынужденных колебаний в установившемся режиме равна частоте:

1. – собственных колебаний; 2. – затухающих колебаний; 3. – вынуждающей силы; 4. – силы трения; 5. – силы тяжести.

22. Логарифмический декремент затухания связан с добротностью колебательной системы Q соотношением:

1. – ; 2. – ; 3. – ; 4. – ; 5. – .

15