модуль 1

ФИЗИКА

Модуль 1.7

ГЛАВА 7 Затухающие и вынужденные колебания

1 Затухающие колебания

Во всякой реальной колебательной системе всегда имеется либо сила трения (в механической системе), либо активное электрическое сопротивление (в колебательном контуре), действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется, колебания будут затухать.

Начнем с рассмотрения механических колебаний. В простейшем случае сила трения (например, сила вязкого трения) пропорциональна скорости:

. (7.1)

Здесь — постоянная, которую мы будем называть коэффициентом трения или коэффициентом сопротивления среды. Знак минус обусловлен тем, что сила и скорость направлены в противоположные стороны, вследствие чего их проекции на ось х имеют разные знаки.

Уравнение второго закона Ньютона при наличии силы трения имеет вид

. (7.2)

Применив обозначения

, , ( 7.3)

напишем уравнение (7.2) следующим образом:

. (7.4)

Отметим, что - собственная частота колебательной системы, т. е. та частота, с которой колебалась бы система в отсутствие трения.

Попробуем искать решение уравнения (7.4) в виде

(7.5)

где некоторая функция от . Дифференцирование по дает:

,

.

После подстановки выражений для , и в уравнение (7.4) и сокращения на отличный от нуля множитель получим дифференциальное уравнение для :

. (7.6)

Решение уравнения (7.6) зависит от знака коэффициента, стоящего при . Рассмотрим случай, когда этот коэффициент положителен (т. е. — трение мала). Введя обозначение

, (7.7)

придем к уравнению

,

решением которого является функция

(см. (5.9) и (5.6)).

Таким образом, в случае малого трения () решением уравнения (7.4) будет функция

. (7.8)

Здесь — постоянные, значения которых зависят от начальник условий, — величина; определяемая формулой (7.7), называется циклической частотой затухающих колебаний.

График функции (7.8) дан на рис.1. Штриховыми линиями показаны пределы, в которых находится смещение колеблющейся частицы.

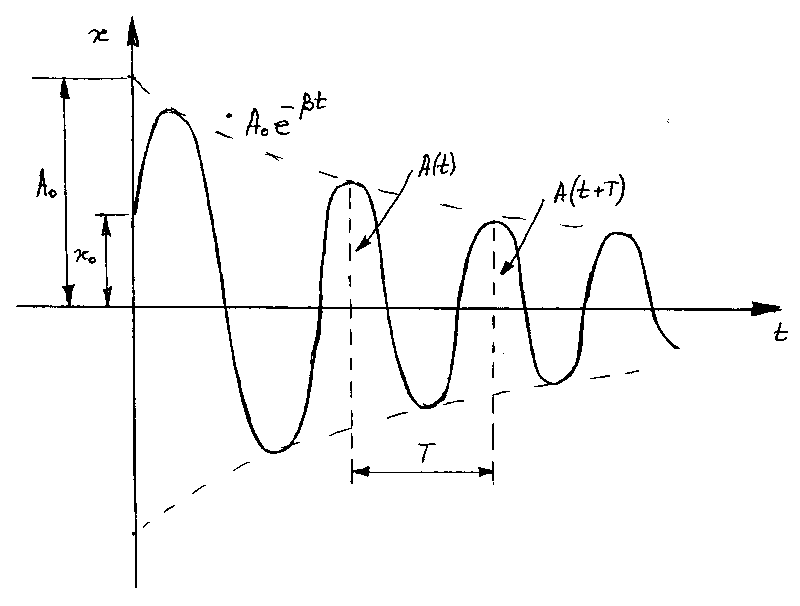
Рис. 1

В соответствии с видом функции (7.8) движение частицы можно рассматривать как гармоническое колебание частоты с амплитудой, изменяющейся по закону

. (7.9)

Верхняя из штриховых кривых на рис. 1 дает график этой функции, причем

представляет собой амплитуду и начальный момент времени. Начальное смещение зависит, кроме, также от начальной фазы : .

Скорость затухания колебаний определяется величиной . которую называют коэффициентом затухания. Найдем время , за которое амплитуда уменьшается в раз. По определению , откуда . Следовательно, коэффициент затухания обратен тому промежутку времени, за который амплитуда уменьшается и раз,

Согласно формуле (7.7) период затухающих колебаний

. (7.10)

При незначительном трении период колебаний практически равен . С ростом коэффициента затухания период колебаний увеличивается.

Отношение значений амплитуды, соответствующих моментам времени, отличающимся на период, равно

Это отношение называют декрементом затухания, а его логарифм — логарифмическим декрементом затухания

. (7.11)

Для характеристики колебательной системы обычно используется логарифмический декремент затухания . Выразив в соответствии с (7.11) через и можно закон убывания амплитуды со временем написать в виде

За время , за которое амплитуда уменьшается в раз, система успевает совершить колебаний. Из условия получается, что . Следовательно, логарифмический декремент затухания обратен числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в раз.

Для характеристики колебательной системы употребляется также величина

(7.12)

называемая добротностью колебательной системы. Она пропорциональна числу колебаний , совершаемых системой за то время , за которое амплитуда колебаний уменьшается

в е раз.

Энергия колебательной системы пропорциональна квадрату амплитуды. В соответствии с этим энергия системы при затухающих колебаниях убывает по закону,

(7.13)

( - значение энергии при ). Как и всякая производная, определяет скорость возрастания , а величина - скорость убывания энергии. Согласно (7.13)

скорость убывания энергии . (7.14)

Если энергия мало изменяется за время, равное периоду колебаний, убыль энергии за период можно найти, умножив выражение (7.14) на :

(напомним, что обозначает приращение, а - убыль энергии). Приняв во внимание формулы (7.11) и (7.12), придем к соотношению

(7.15)

из которого следует, что при слабом затухании колебаний добротность с точностью до множителя равна отношению энергии, запасенной в системе в данный момент, к убыли энергии за один период колебаний.

Из формулы (7.10) вытекает, что при период колебаний обращается в бесконечность, т. е. движение перестает быть периодическим. В случае, когда (трение велико), общее решение уравнения (7.4) имеет вид

, (7.16)

где , , — постоянные, значения которых зависят от начальных условий.

(В этом можно убедиться подстановкой функции (7.16) в уравнение (7.4).) Следовательно, движение носит апериодический (непериодический) характер— выведенная из положения равновесия система возвращается обратно, не совершая колебаний. На рис. 2 показаны два возможных способа возвращения системы в положение равновесия при апериодическом движении. Каким из этих способов приходит система в положение равновесия, зависит от начальных условий.

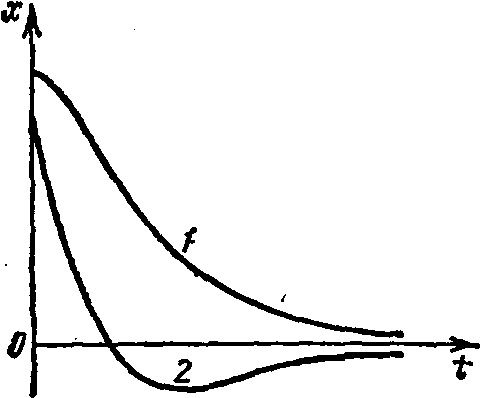
Рис. 2

2 Вынужденные колебания

Допустим, что механическая колебательная система подвергается действию внешней силы, изменяющейся со временем по гармоническому закону;

. (7.17)

В этом случае уравнение второго закона Ньютона имеет вид

.

Введя обозначения (7.3), преобразуем уравнение следующим образом:

. (7.18)

Здесь — коэффициент затухания, — собственная частота колебательной системы, — частота вынуждающей силы.

Дифференциальное уравнение (7.18) описывает вынужденные колебания. Из теории линейных дифференциальных уравнений с постоянными коэффициентами известно, что общее решение неоднородного уравнения (т.е. уравнения, в правой части которого стоит не равная тождественно нулю функция от ) равно сумме общего решения соответствующего однородного уравнения (т. е. того же уравнения, в котором правая часть принята равной тождественно нулю) и частного решения неоднородного уравнения. Общее решение однородного уравнения мы уже знаем, оно имеет вид

, (7.19)

где (см. формулу (7.8)).

Остается найти частное (т. е. не содержащее произвольных постоянных) решение уравнения (7.18). Попробуем искать это решение в виде

, (7.20)

где — неизвестный пока сдвиг фаз между силой и вызываемыми ею колебаниями. Попытаемся выяснить, не существует ли таких значений и , при которых функция (7.20) удовлетворяет уравнению (7.18). Для этого подставим в уравнение (7.18) выражение (7.20) и его производные

, (7.21)

, (7.22)

разворачивая одновременно и по формулам для синуса и косинуса разности:

Сгруппировав соответствующим образом члены уравнения, получим

(7.23)

Для того чтобы уравнение (7.23) удовлетворялось при любых значениях , коэффициенты при и в обеих частях уравнения должны быть одинаковыми. Отсюда получаются условия

, (7.24)

, (7.25)

Из этих соотношений можно найти значения и , при которых функция (7.20) удовлетворяет уравнению (7.18). Возведя равенства (7.24) и (7.25) в квадрат и сложив их друг с другом, получим

,

откуда

. (7.26)

Из уравнения (7.25) следует, что

. (7.27)

Подставив в (7.20) значения и , определяемые формулами (7.26) и (7.27), получим частное решение неоднородного уравнения (7.18):

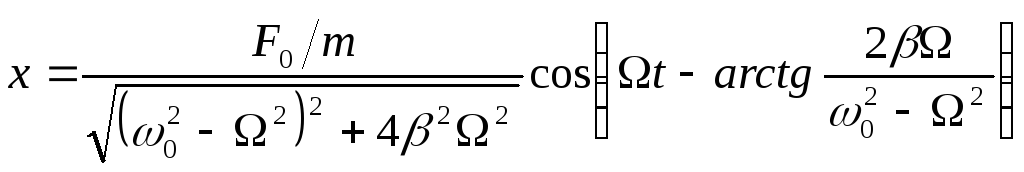. (7.28)

Функция (7.28) в сумме с (7.19) дает общее решение уравнения (7.18). Слагаемое (7.19) играет заметную роль только в начальной стадии процесса, при установлении колебаний (рис. 3). С течением времени из-за экспоненциального множителя роль слагаемого (7.19) уменьшается, и по прошествии достаточного времени им можно пренебречь, сохранив в решении только слагаемое (7.28), которое описывает установившиеся вынужденные колебания. Отметим, что на рис.3 изображен простейший случай установления колебаний.

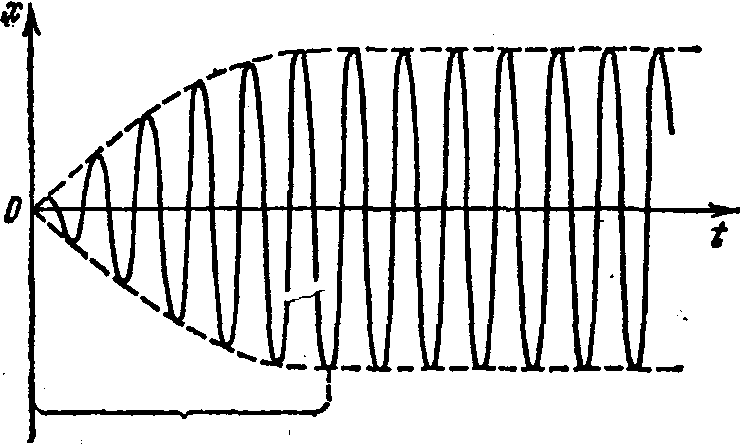
установление колебаний

Рис. 3

Обсудим полученные результаты. Из формулы (7.28) следует, что установившиеся вынужденные колебания представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда колебаний пропорциональна амплитуде силы. Для данной колебательной системы (для заданных и амплитуда зависит от частоты силы). Колебания отстают по фазе от силы, причем отставание также зависит от частоты силы.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой частоте амплитуда достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при данной частоте. Это явление называется резонансом, а соответствующая частота — резонансной частотой.

Чтобы определить резонансную частоту , нужно найти максимум функции (7.26) или, что то же самое, минимум выражения, стоящего под корнем в знаменателе. Продифференцировав это выражение по и приравняв производную нулю, получим условие, определяющее

.

Это уравнение имеет три решения: и . Решение, равное нулю, соответствует максимуму знаменателя (т. е. минимуму амплитуды). Из остальных двух решений отрицательное должно быть отброшено, как не имеющее физического смысла (частота не может быть отрицательной). Таким образом, для резонансной частоты получается одно значение:

(7.29)

Подставив это значение в (7.26), получим выражение для амплитуды при резонансе:

(7.30)

Из этого выражения следует, что в отсутствие трения амплитуда при резонансе обращалась бы в бесконечность. Согласно (7.29) резонансная частота при тех же условиях (при ) совпадает с собственной частотой колебаний системы

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (или, что то же самое, от частоты колебаний) показана графически на рис. 5.

Кривые на графике соответствуют различным значениям параметра . В соответствии с (7.29) и (7.30), чем меньше , тем выше и правее лежит максимум резонансной кривой. При очень большом затухании (таком, что ) выражение для резонансной частоты становится мнимым. Это означает, что резонанс в этом случае не наблюдается – с увеличением частоты амплитуда монотонно убывает (см. рис. 5).

Рис. 5

Изображенная на рис. 5 совокупность графиков функции (7.26) называется резонансными кривыми. По поводу этих кривых можно сделать следующие замечания. При стремлении частоты к нулю все кривые приходят к одному и тому же предельному значению, равному , т. е. . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы . При стремлении к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия. Наконец, отметим, что чем меньше , тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем острее получается максимум.

Согласно формуле (7.30) при малом затухании (т. е. при ) амплитуда при резонансе

.

Разделим это выражение на смещение из положения равновесия под действием постоянной силы , равное . В результате получим, что

, (7.31)

(см. формулу (7.12)). Следовательно, добротность показывает, во сколько раз амплитуда при резонансе превышает смещение системы из положения равновесия под действием постоянной силы, модуль которой равен амплитуде вынуждающей силы (это справедливо лишь при небольшом затухании).

Вынужденные колебания отстают по фазе от вынуждающей силы, причем отставание лежит в пределах от 0 до . Зависимость от при разных значениях показана

на рис. 6. Частоте соответствует . Резонансная частота меньше собственной

(см. формулу (7.29)), поэтому в момент резонанса . При слабом затухании и значение при резонансе можно считать равным .

Рис. 6

Явление резонанса приходится учитывать при конструировании машин и различных сооружений. Резонансная частота этих устройств не должна быть близка к частоте возможных внешних воздействий. Например, резонансная частота вибраций корпуса корабля и крыльев самолета должна сильно отличаться от частоты колебаний, которые могут возбуждаться вращением гребного винта или пропеллера. Иначе возбуждаются вибрации, которые могут вызвать катастрофу.

Задачи

Задача 1 Амплитуда затухающих колебаний за один период уменьшается в 3 раза. Определить логарифмический декремент затухания и найти, при каких значениях фазового угла достигается максимальное смещение от положения равновесия.

Решение

По определению логарифмический декремент затухания равен

.

Из условия задачи следует, что

= 1,09.

Для ответа на второй вопрос запишем уравнение затухающих колебаний.

и вычислим производную ,

Условие максимума имеет вид

,

где введено обозначение фазового угла

,

а - момент времени, когда .

Таким образом,

.

Подставляем численные значения, находим

, .

Задача 2 Стальной шарик диаметром = 2 см совершает на легкой пружине вертикальные колебания в воздухе с циклической частотой = 5 рад/с. Если шарик опустить в жидкость, то частота уменьшится до величины = 4 рад/с. Определить кинематическую вязкость жидкости .

Решение

Из формулы и имеем:

, ,

отсюда

.

Кинетический коэффициент вязкости можно найти, используя формулу Стокса:

,

откуда

.

Подставляя численные значения ( кг/м³), получаем

.

Задача 3 Найти добротность математического маятника длины = 50 см, если за время = 5,2 мин его энергия колебаний уменьшается в раз.

Решение

Прежде всего выясним, можно ли в данном случае пользоваться формулой , справедливой для малого затухания (). Если ~ , то из условия задачи следует, что