Строительная механика / Учебник СМ Саргсян / П17

,

где

6.5. Расчет тонкостенного стержня открытого профиля (задача 17)

Для тонкостенного стержня открытого профиля, изображенного на рис. 6.8, а, при следующих исходных данных: H = 12.5×10^-2 м; B = 19×10^-2 м; l = 2 м; d = 1×10^-2 м; P = 1 кН; E  = 2×10⁵ МПа; G = = 8×10⁴ МПа, требуется:

Рис. 6.8

1. Определить площадь, положение центра тяжести, главные центральные моменты инерции поперечного сечения;

2. Найти положение центра изгиба;

3. Определить момент инерции при чистом кручении J_кр и секториальные характеристики сечения;

4. Вычислить изгибно-крутильную характеристику ;

5. Построить эпюры поперечной силы Q_x, изгибающего момен­та M_y, момента чистого кручения M_g, изгибно-крутящего момента M_w, бимомента B_w ;

6. Построить эпюры нормальных напряжений s_z, s_w и их сум­марную эпюру.

Решение

1. Определение площади, положения центра тяжести и главных центральных моментов инерции

Вычислим расчетные размеры сечения стержня (рис. 6.8, б, в), приняв в дальнейших расчетах:

м = const; м;

м.

Тогда

м².

В выбранной системе координат x₁y₁, определим положение центра тяжести сечения: y_c = 0;

Для этого построим эпюру координат x₁ (рис. 6.9, а) и вычис­лим статический момент сечения относительно оси y₁ :

м³.

Тогда координата центра тяжести сечения будет равна:

м.

Для вычисления главных центральных моментов инерции пред­варительно построим эпюру координат x и y (рис. 6.9, б, в). С при­менением этих эпюр, определяются:

м⁴;

м⁴.

Рис. 6.9

2. Определение положения центра изгиба

Вначале построим эпюру секториальных координат площади w_В , в характерных точках (1, 2, 3, 4) профиля, выбрав произволь­ный полюс в точке B (рис. 6.9, г):

м²; ;

м².

Координаты центра изгиба вычисляем по формулам (6.5).

Используя эпюры w_В  и y и применяя правило Верещагина, вычисляем секториально линейный статический момент:

= -116.64×10^-8 м⁵.

Тогда координата центра изгиба по вертикальной оси прини­мает значение:

м.

Координата центра изгиба по горизонтальной оси вычисляется

Так как эпюра x симметрична, а эпюра w_B обратно симметрич­на относительно x, то по правилу Верещагина секториально-ли­нейный статический момент равен нулю, т.е.:

.

Cледовательно, y_А = 0 и поэтому центр изгиба лежит на оси x.

Вычислим постоянную D, предварительно построив эпюру сек­ториальных площадей w' (рис. 6.9, д).

При этом полюс расположим в центре изгиба (т. А). За начало отсчета возьмем точку 3 (произвольно):

м² ;

м² ;

м² .

Постоянную D вычисляется по формуле (6.6):

Далее вычисляем секториально статический момент , как произведение площади эпюры w' на d :

м⁴ .

В этом случае величина постоянной D будет равна:

м² .

Далее, используя зависимость (6.7), вычисляем секториальные координаты характерных точек профиля:

м² ;

м² ;

м² ;

м² .

По полученным координатам строим эпюру w (рис. 6.9, е).

3. Определить момент инерции при чистом кручении и секториальные характеристики сечения

Для корытообразного профиля поперечного сечения бруса (рис. 6.8, б), имеем:

м⁴ .

Cекториальный момент инерции J_w вычисляем по эпюре w (рис. 6.9, е):

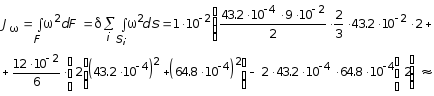
»м⁶ .

4. Определение изгибно-крутильной характеристики a

Изгибно-крутильную характеристику a вычисляем по формуле:

м^-1 .

5. Построение эпюр поперечной силы Q_x , изгибающего момента M_y , момента чистого кручения M_g , изгибно-крутящего момента М_w и бимомента В_w

В рассматриваемом примере:

м;    кН = 95 Н;

al = 1.3×2 = 2.6;  ch al = 6.7690;  a× ch al = 1.3×6.7690 = 8.7997 м^-1.

Тогда, согласно (6.25), получим:

Предварительно разбив тонкостенный брус по длине на 5 рав­ных частей, для этих сечений численные значения величин Q_x , M_y , M_g , М_w и В_w приведены в табл. 6.2.

По результатам табл. 6.2 строим эпюры Q_x , M_y , M_g , М_w и В_w (рис. 6.10). При этом в случае действия на брус сосредоточенной силы, во всех сечениях выполняется следующее условие: M_g  + М_w = Р е = const.

Таблица 6.2

z, м	a z	sh a z	ch a z	Qx, Н	My, Н×м	Mg, Н×м	Мw, Н×м	Вw , Н×м2
0.00	0.00	0.0000	1.0000	1000	0	80.97	14.03	0
0.40	0.52	0.5438	1.1383	1000	400	79.03	15.97	5.87
0.80	1.04	1.2379	1.5913	1000	500	72.67	22.33	13.37
1.20	1.56	2.2743	2.4845	1000	1200	60.14	34.86	24.50
1.60	2.08	3.9398	4.0647	1000	1600	37.96	57.04	42.56
2.00	2.60	6.6947	6.7690	1000	2000	0.00	95.01	72.32

6. Построить эпюры нормальных напряжений s_z, s_w и их суммарную эпюру

Нормальные напряжения зависят от внутренних силовых фак­торов M_y и B_w согласно выражения (6.11). Опасным сечением явля­ется сечение в заделке, так как в нем действуют наибольшие по величине M_y и B_w (рис. 6.10, в, д). Нормальные напряжения от изгиба (рис. 6.11, а) определяем по формуле:

Па = -303.8 x₁ МПа.

Рис. 6.8 Рис.6.9

В точке 1: x₁ = 8.57×10^-2 м, = -303.8×8.57×10^-2= -26 Мпа.

В точке 2: x₁ = -3.43×10^-2 м, = -303.8×(-3.43×10^-2) = 11.94 МПа.

В точке 3: x₁ = -3.43×10^-2 м, = -303.8×(-3.43×10^-2) = 11.94 МПа.

В точке 4: x₁ =8.57×10^-2 м, = -303.8×8.57×10^-2= -26 МПа.

По найденным данным строим эпюру s_z (рис. 6.11, а).

Нормальные напряжения в точках профиля от действия бимо­мента В_w вычисляем по формуле:

Па = МПа.

В точке 1: МПа.

В точке 2: МПа.

В точке 3: МПа.

В точке 4: МПа.

По полученным данным строим эпюру s_w. Суммарные нор­мальные напряжения в опасном сечении тонкостенного стержня от совместного действия изгиба и стесненного кручения вычислим пу­тем сложения эпюр s_z и s_w по формуле: s = s_z + s_w .

В точке 1: s₁ = -26 - 12.55 = -38.55 МПа.

В точке 2: s₂ = 11.94 + 8.37 = 20.31 МПа.

В точке 3: s₃ = 11.94 - 8.37 = 3.57 МПа.

В точке 4: s₄ = -26 + 12.55 = -13.45 МПа.

Суммарная эпюра нормальных напряжений s приведена на рис. 6.11, в.

6.6. Вопросы для самоконтроля

1. Дайте определение тонкостенного стержня как геометрической фигуры.

2. Что называется депланацией сечения?

3. Дайте пояснение, что такое свободное и стесненное кручение соответственно.

4. Дайте определение серединной линии поперечного сечения тонкостенного стержня.

5. Дайте определение понятия секторальной площади.

6. Какая точка называется секторальным полюсом.

7. Сформулируйте понятие секторально статический момент сечения, секторально линейный момент площади поперечного сечения и секторальный момент инерции поперечного сечения тонкостенного стержня.

8. Дайте пояснение понятия главной секторальной площади.

9. Дайте пояснение понятия бимомента.

10. Сформулируйте выражения перемещения, нормальные и касательные напряжения, возникающие при общем характере нагружения тонкостенного стержня.

Раздел 7.  ПЛАСТИНЫ И ОБОЛОЧКИ

7.1. Основные положения теории оболочек

Большинство элементов инженерных конструкций в расчетной схеме, подлежа­щих расчету на прочность, как это уже было отмечено, связаны с расчетом бруса, пластинок или оболочек.

Предыдущие разделы были достаточно подробно посвящены вопросам расчета стержней и стержневых систем. Настоящий раз­дел книги посвящен различным вопросам расчета пластинок и оболочек.

Под оболочкой понимается тело, одно из измерений которого (толщина) значительно меньше двух других. Геометрическое место точек, равноотстоящих от обеих поверхностей оболочки, носит наз­вание срединной поверхности.

Если срединная поверхность оболочки является плоскостью, то такую оболочку называют пластиной.

Геометрическая форма объектов, которые могут быть причислены к оболочкам или пластинам, чрезвычайно разнообразна: в машиностроении - это корпуса всевозможных машин; в гражданском и промышленном строительстве - покрытия и перекрытия, навесы, карнизы; в кораблестроении - корпуса судов, сухих и плавучих доков; в авиастроении - фюзеляжи и крылья самолетов; в подвижном составе железнодорожного транспорта, кузова вагонов, цистерны, несущие конструкции локомотивов; в атомной энергетике - защитная конструкция атомных станций, корпуса реакторов и т.д.

Если срединная поверхность оболочки образует поверхность вращения в форме цилиндра, то оболочку называют цилиндриче­ской.

К схеме осесимметричной цилиндрической оболочки сво­дится очень много инженерных конструкций, в том числе: котлов, баков, неф­тепроводов, газопроводов, деталей машин и др.

244