Проверка нормальности распределения выходной величины

Результаты предварительной серии опытов представлены в таблице:

Результаты предварительной серии опытов.

22,958	21,719	22,949
21,607	22,102	22,807
22,614	21,342	22,272
23,135	21,802	21,437
23,701	24,204	23,133
22,259	20,402	23,237
22,499	22,434	23,014
21,135	23,916	23,853
23,149	21,819	21,258
23,223	21,976	21,43
23,226	20,778	21,318
21,446	20,604	24,547
22,068	22,49	22,435
21,225	21,838	22,957
23,147	22,603	22,633
24,522	22,862	23,101
22,624	21,761	22,703
22,722	22,881	23,824
23,423	21,727	22,113
20,925	23,143	22,583

Разобьем диапазон от 20,402 до 24,547 на интервалы равной длины. По формуле нахождения интервалов находим 7 интервалов.

Длина каждого интервала:

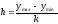
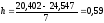
Среднее значение выходной величины будет равно:

=

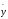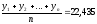
_{Для того чтобы вычислить выборочную дисперсию:}

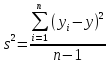
необходимо найти границы интервалов и их середины. Достаточно знать, в какой интервал попадает каждое значение случайной величины:

Номер интервала	Границы интервала	Середина интервала	Число наблюдений в интервале (mi)	Относительная частота pi = m1/m
1	20,402 … 20,994	20,698	4	0,06667
2	22,994 … 21,586	21,290	8	0,13333
3	21,586 … 22,178	21,882	11	0,18333
4	22,178 … 22,771	22,475	13	0,21667
5	22,771 … 23,363	23,067	16	0,26667
6	23,363 … 24,955	23,659	5	0,08333
7	24,955 … 24,547	24,251	3	0,05000

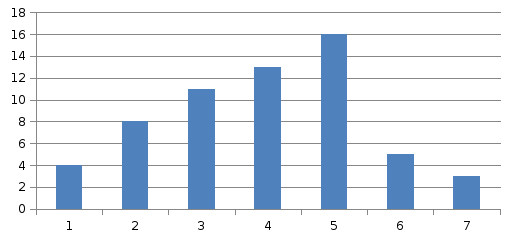
Т.к. сумма всех относительных частот равна единице, то площадь гистограммы тоже равна единице. С увеличением числа опытов, n значение каждой частоты становится всё ближе к соответствующей вероятности p_i.

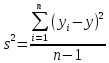=0,842

Предполагается, что выходная величина подчиняется нормальному закону распределения. Это предположение можно проверить разными способами. Наиболее строгим из них является применение критерия χ² Пирсона. Для этого необходимо иметь выборку достаточно большого объема: n> 50 – 150. Диапазон изменения выходной величины в этой выборке разбивается на l интервалов так, чтобы эти интервалы покрывали всю ось от -до +и в каждый интервал при этом попало не менее пяти значений выходной величины. Подсчитывают количествоm_i наблюдений, попавших в каждый интервал. Затем вычисляют теоретические попадания случайной величины в каждый i-й интервал. Для этого используют формулу

p_i = Ф(z₂) – Ф(z₁), где

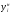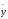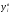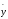z₁ = (-) / s; z₂ = (-) / s;

где - среднее арифметическое выборки;s – среднее квадратическое отклонение выборки; 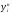- нижняя границаi-го интервала; 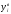- верхняя границаi-го интервала; Ф(z) – нормированная функция Лапласа:

Ф(z) =

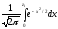
Значения ее для z = z₁ и z = z₂ определяют из таблиц. При отыскании значений этой функции для отрицательных значений аргумента следует иметь в виду, что функция Ф(z) нечетная:

Ф(- z) =1 - Ф(z).

Следующим этапом является вычисление величины χ² по формуле

χ² = .

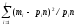По выбранному уровню значимости q и числу степеней свободы k = l – 3 из таблицы отыскивают . Гипотезу о нормальности распределения можно принять, если.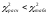

Вычисления удобно вести заполняя таблицу:

Вспомогательная таблица для расчета критерия χ² Пирсона.

Номер нтервала	yiн	yiв	mi	z1	z2	Ф0(z1)	Ф0(z2)	pin	(mi-pin)2	(mi-pin)2/pin
1	2	3	4	5	6	7	8	9	10	11
1	20,402	20,994	4	-2,215	-1,570	0,01355	0,03836	1,489	6,307	4,2370
2	20,994	21,586	8	-1,570	-0,925	0,05821	0,17879	7,235	0,586	0,0809
3	21,586	22,178	11	-0,925	-0,280	0,17879	0,38974	12,657	2,746	0,2169
4	22,178	22,771	13	-0,280	0,366	0,38974	0,64058	15,050	4,204	0,2793
5	22,771	23,363	16	0,366	1,011	0,50399	0,84375	20,386	19,233	0,9435
6	23,363	23,955	5	1,011	1,656	0,84375	0,85543	0,701	18,483	26,3743
7	23,955	24,547	3	1,656	2,301	0,85543	0,989280	8,031	25,311	3,1517

Данные выборки разобьем на 7 интервалов, границы которых указаны во втором и третьем столбцах. В четвертом столбце приведено количество наблюдений, попавших в каждый интервал. Далее по данным таблицы

вычислены среднее 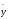и стандартs выборки.

Среднее квадратическое отклонение:

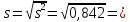0,918

По формулам рассчитываем значения z₁ и z₂ для каждого интервала (пятый и шестой столбец)

По таблице находим нормированную функцию Лапласа.

Согласно формуле вычисляем теоретическое попадание случайной величины в каждый i-й интервал и заполняем столбец 9 таблицы.

Искомую величину 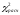получают суммированием значений последнего столбца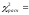2.923.

Выберем уровень значимости q = 0,05,

число степеней свободы k = 7-3 = 4.

По найденным величинам q и f из таблицы отыскиваем - гипотеза о нормальности распределения принимается. По результатам проверки строим гистограмму распределения, а так же теоретическую кривую плотности нормального распределения.