Глава 15. Операционное исчисление.
§ 1. Преобразование Лапласа.
Пусть
- функция (которая, вообще говоря, может
принимать и комплексные значения)
действительного аргумента
,
такая, что:
1)
она кусочно-непрерывна на
,
т.е. непрерывна на данном промежутке,
за исключением конечного числа точек,
где она имеет разрывы первого рода; 2)
существуют положительные числа
и
такие, что для всех
справедливо неравенство
.
Преобразованием
Лапласа
функции
называется функция
комплексного переменного
,
,
определяемая равенством :
.
При этом функция
называется оригиналом,
а функция
- его изображением.
Соответствие между оригиналом и его
изображением символически записывается
в виде
или
.
Если функция
задана на всей числовой прямой (
),
то вместо неё всюду в дальнейшем, без
специальных оговорок, будем рассматривать
функцию
,
где
- единичная
функция Хевисайда, т.е.
будем считать
при
,
причём
.
При нахождении
изображений и оригиналов широко
применяются таблица
изображений
преобразования Лапласа и его свойства,
а также формулы:
;
;
;
.
В задачах 15.1-15.4 пользуясь определением преобразования Лапласа, найти изображения следующих функций:
15.1
15.2
15.3
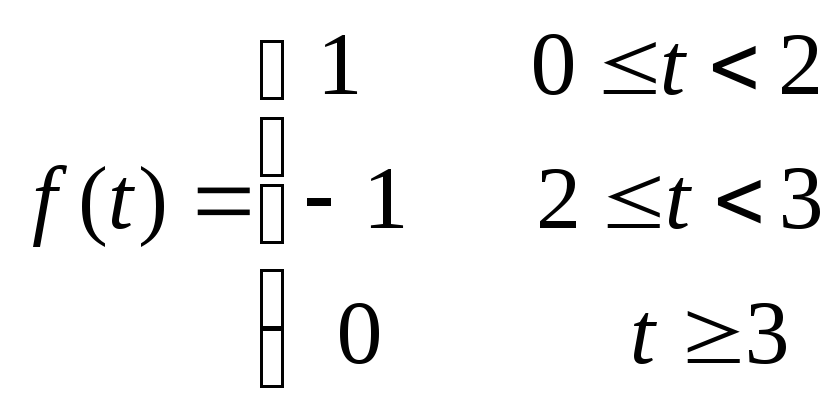15.4
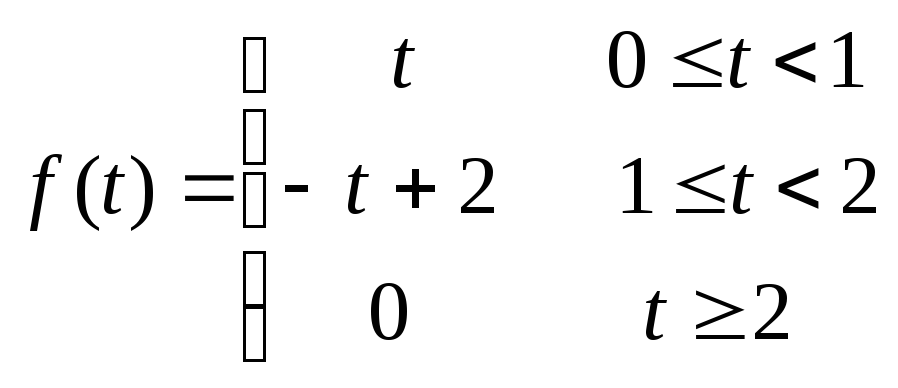
Таблица изображений преобразования Лапласа
|
|
|
|
|
1. |
1 |
1/p |
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
6. |
|
|
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
|
|
11. |
|
|
|
12. |
|
|
|
13. |
|
|
|
14. |
|
|
|
15. |
|
|
|
16. |
|
|
|
17. |
|
|
|
18. |
|
|
|
19. |
|
|
|
20. |
|
|
Cвойства преобразования Лапласа.
1.Аддитивность:
2.Однородность:
3.Теорема
смещения:
4.Теорема
запаздывания:
5.Теорема
о свертке:
где
6.Теорема о дифференцировании изображения:
7.Теорема о дифференцировании оригинала:
8.Теорема об интегрировании оригинала:
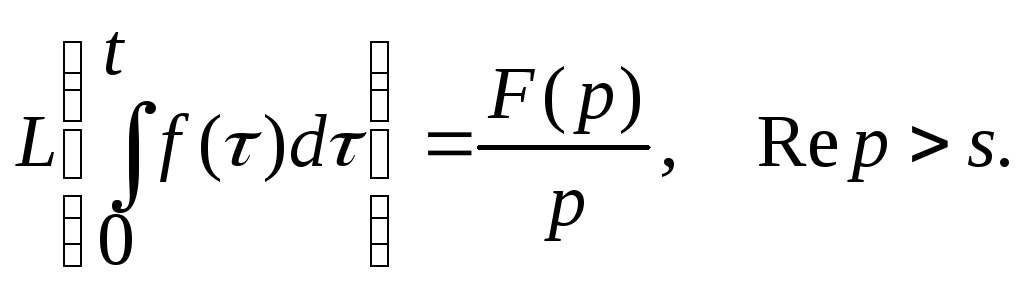
9.Теорема
об интегрировании изображения:
В задачах 15.5-15.22 используя таблицу изображений преобразования Лапласа, найти изображения следующих функций:
15.5
15.6
15.7
15.8
15.9
15.10
15.11
15.12
15.13
15.14
15.15
15.16
15.17
15.18
15.19
15.20
15.21
15.22
В задачах 15.23-15.28 используя теорему смещения, найти изображения следующих функций:
15.23
15.24
15.25
15.26
15.27
15.28
В задачах 15.29-15.34 используя теорему о дифференцировании изображения, найти изображения следующих функций:
15.29
15.30
15.31
15.32
15.33
15.34
В задачах 15.35-15.40 используя теорему об интегрировании изображения, найти изображения следующих функций:
15.35
15.36
15.37
15.38
15.39
15.40
В задачах 15.41-15.46 используя теорему об интегрировании оригинала, найти изображения следующих функций:
15.41
15.42
15.43
15.44
15.45
15.46
В задачах 15.47-15.52 используя теорему о свёртке, найти изображения следующих функций:
15.47
15.48
15.49
15.50
15.51
15.52
В задачах 15.53-15.62 используя теорему запаздывания, найти изображения следующих функций:
15.53
15.54
15.55
15.56
15.57
15.58
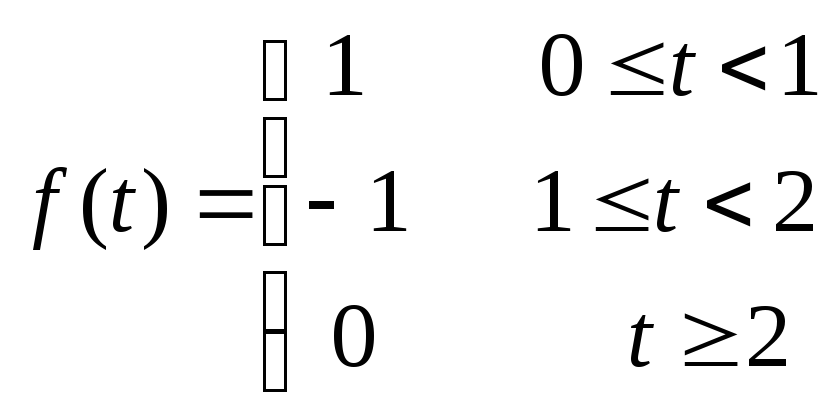
15.59
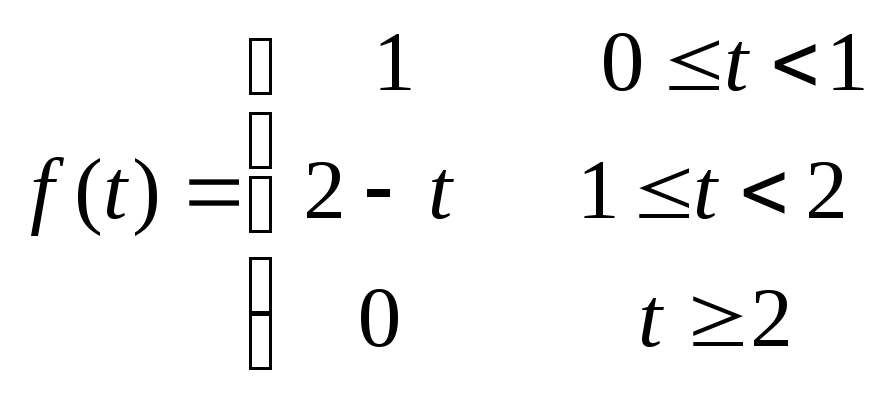15.60
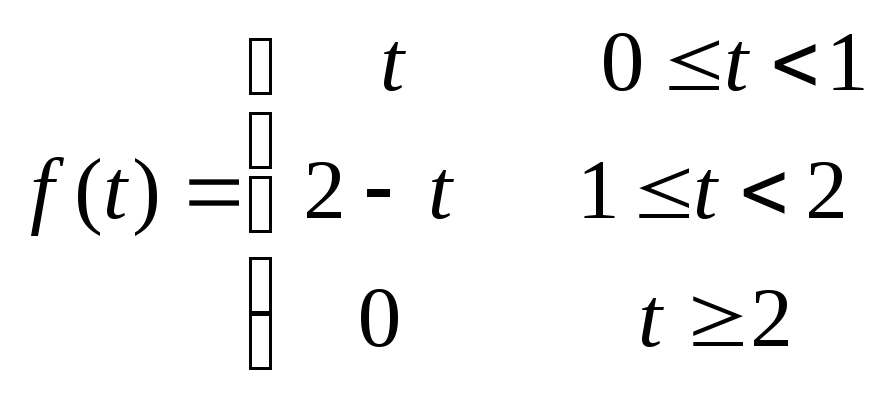
15.61
15.62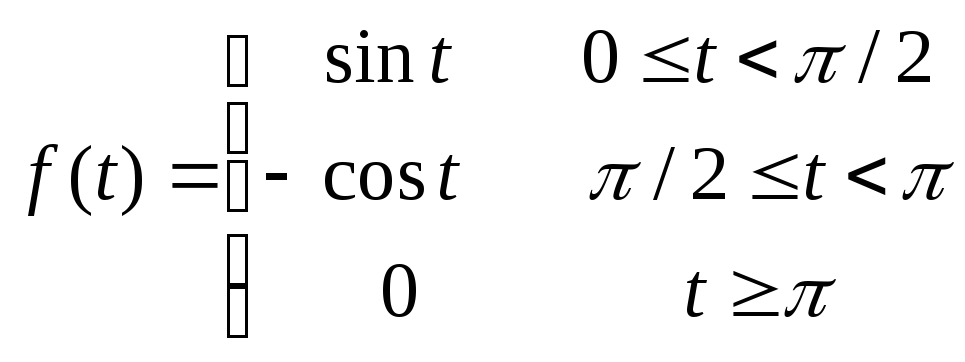
В задачах 15.63-15.74 используя таблицу изображений преобразования Лапласа, найти оригиналы для изображений:
15.63
15.64
15.65
15.66
15.67
15.68
15.69
15.70
15.71
15.72
15.73
15.74
В задачах 15.75-15.80 используя теорему запаздывания, найти оригиналы для следующих изображений:
15.75
15.76
15.77
15.78
15.79
15.80
