2 3

4

V2

5. 6

Коэффициент передачи управляемости вентиля 2И-НЕ CTF = 0.5.

Введем обозначения для двух вентилей V1 и V2.

Запишем выражения для управляемости всех входных узлов:

CY(V1, 1) = 1, 0

CY(V1, 2) = x (сначала неизвестна)

СY(V2, 4) = y сначала неизвестна)

CY(V2, 5) = 1, 0

Все входы в схеме асинхронные, можем записать выражение для управляемости выходов в учетом принятых обозначений и полученных выше формул:

CY(v1, 3) = y = ctf [cy(1) + CY(2)]/2 = 0.5(1+x)/2 ,

CY(V2, 6) = x = CTF[CY(4) + CY(5)]/2 = 0.5(1+y)/2 .

Решение системы уравнений будет x = y = 0.33, то есть cy(выходов) = 0,33.

Наблюдаемость (OY) – мера, характеризующая способность схемы к передаче информации о логическом состоянии данного узла на один или несколько выходов. Наблюдаемость первичного входа =1, наблюдаемость в самом узле =1. Величина OY уменьшается по мере прохождения сигналов вдоль активизированного пути к первичным выходам.

Коэффициент передачи наблюдаемости OTF – количественная мера уменьшения OY входного узла устройства по мере продвижения к выходу по активизированному пути. При этом все остальные входные узлы устройства должны быть управляемы.

OY(на выходе) = OTF  OY(на входе)  g(CY активизирующих входов).

OY – величина, зависящая от условий установки фиксированных значений на некоторых или всех входах, позволяющих активизировать определенный путь для прохождения сигнала по схеме.

Вычисление OTF.

Коэффициент передачи наблюдаемости от входа I к выходу Q OTF(I-Q) должен быть равен нулю, если нет пути транспортировки неисправности между этими точками, и, с другой стороны, OTF(I-Q) = 1, если это происходит независимо от состояний активизирующих входов.

где N(SP) – суммарное число различных активизированных путей от I к Q ,

N(IP) - - « - « неактивизированных путей - « - .

ПРИМЕРЫ. Переменные на входах A,B,C и т.д., Z – выход.

1. Cхема инвертора, НЕ-А. A,Z. N(SP A-Z) = 1

N(IP A-Z) = 0

OTF(A-Z) = 1.

2. Cхема 2И-НЕ. A,B,Z

N(SP A-Z) = 1

N(IP A-Z) = 1

OTF(A-Z) = 0.5, OTF(B-Z) = 0.5 (cимметрия схемы).

3. Cхема ИЛИ-НЕ - аналогично предыдущей схеме, OTF(A-Z) = OTF(B-Z) = 0.5.

4. Cхема «исключающего ИЛИ»или «неэквивалентность». A,B,Z. ().

N(SP:A-Z) = 2 OTF(A-Z) = 1,

N(IP:A-Z) = 0 OTF(B-Z) = 1 (симмертия) .

Наблюдаемость входа.

A B C

V1 v2

OY(A-A) – наблюдаемость узла А в узле А = 1 (по определению);

OY(A-B) – -“ -“ -“ узла А в узле В,

OY(B-C) – В в С,

OY(A-C) – А в С .

В общем виде:

OY(J-Q) = OY(J-J) OTF(J-Q) CY(cp.),

[(CY: i асинхр.активизир-щих входов)+ {(СY: такт. входов) (СY: j синхр. aктивизир-х входов)}].

Так как наблюдаемость мультипликативна, ее не нужно вычислять для каждого узла.

Для предыдущего примера имеем:

OY(A-C) = OY(A-A) OY(A-B) OY(B-C),

что эквивалентно математически

OY(A-C) = OY(C-C)  OY(B-C)  OY(A-B),

Так как OY(A-A) = OY(C-C) = 1.

Ветвление выхода.

В устройстве с ветвлениями можно наблюдать искомые состояния на первичных выходах. Рассмотрим пример:

V1 Пвых 1

Х

V2 Пвых 2

В этой схеме состояние узла Х можно наблюдать на выходах 1 и 2. При активизации одного из возможных путей, состояние любого узла можно наблюдать на первичных выходах, что можно рассчитывать при помощи следующего выражения:

OY (составная ) = 1 - [1 – OY(каждого Пвых )]

Для нашего примера

OY(X – (Пвых1, Пвых2 )) = 1 – [1 – OY(X – Пвых1)]  [1 – OY(X – Пвых2)].

Сходящиеся ветвления.

Путь 1 1 А 2 В путь 1 1

Х

Х4 Пвых 3

2

3 С путь 2 Пвых

путь 2

Для путей неравной длины нужно выбрать значение OY(X - Пвых), соответствующее кратчайшему путь от Х к Пвых (путь 2 для левого рисунка). Остальные пути блокируются, чтобы информация не сходилась.

Для путей равной длины вычисляется OY(X - Пвых), для обоих путей выбирается путь с наибольшим значением наблюдаемости, другие пути блокируются.

Вычисление тестопригодности.

TY(узла) = CY(узла)  OY(узла)

TY(схемы) = (TY(узлов))/(число узлов)

Процедура вычислений TY.

1. Подготовить и проверить схемные соединения.

2. Вычислить управляемость CY узлов от Пвх через схему. Составить библиотеку значений CTF.

3. Вычислить наблюдаемость OY узлов от Пвх до Пвых. Составить библиотеку значений OTF.

4. Вычислить узловые TY.

5. Вычисление средних значений 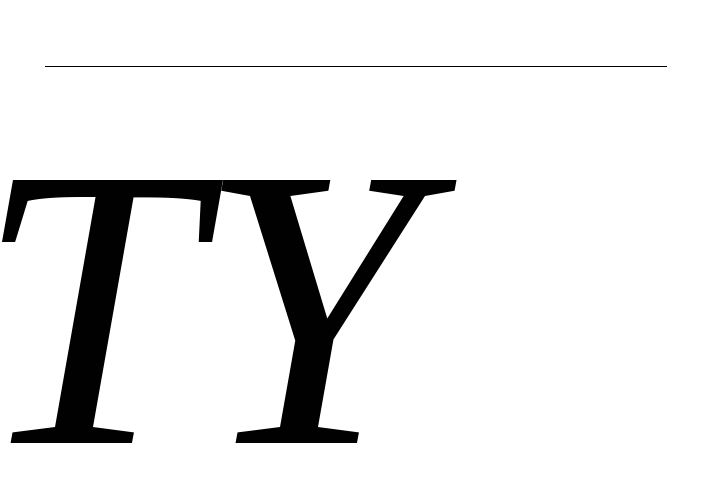и интерпретация результатов.

Количественная оценка проектируемых схем.

Численные значения тестопригодности TY помогают сравнительному анализу тестопригодности узлов схемы. Приоритетны значения управляемости CY, затем – наблюдаемости OY.

Величину CY можно увеличить введением дополнительных непосредственно управляемых входов.

Величину OY можно повысить, если улучшить доступ к данной части схемы введением дополнительных контрольных точек.

ДОМАШНЕЕ ЗАДАНИЕ

1. Ознакомиться с теоретическими сведениями по тестопригодности ИС.

2. Ознакомиться с заданием на лабораторную работу.

ЗАДАНИЕ НА ЛАБОРАТОРНУЮ РАБОТУ

Задание выполняется для схемы, спроектированной в лабораторной работе №3.

1. Рассчитать параметры тестопригодности для схемы, исследованной в работе №3 ,по формулам, представленным в теоретическом разделе.

2. Сравнить значения CY, OY и TY по узлам схемы.

3. Вычислить для всей схемы величины

4. Дать рекомендации по увеличению значений параметров тестопригодности исследуемой схемы.

ПОРЯДОК ВЫРОЛНЕНИЯ РАБОТЫ

1. Провести расчет величины CY для всех узлов схемы из работы №3. Вычислить также величины OY и TY для всех узлов схемы.

2. Заполнить таблицу результатов выполнения работы.

3. Исследовать возможность увеличения значений параметров тестопригодности исследуемой схемы.

4. Оформить отчет по работе.

Таблица

РЕЗУЛЬТАТЫ ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ №4

№№ УЗЛОВ	ВЕЛИЧИНА CY	ВЕЛИЧИНА OY	ВЕЛИЧИНА TY
1(Пвх)
2
…
N (Пвых)

СОДЕРЖАНИЕ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ

Отчет по лабораторной работе должен содержать:

1. Исследуемую структурную схему.

2. Значения параметров CTF и OTF для библиотечных элементов, на которых построена схема.

3. Заполненную таблицу с результатами выполнения расчетов (либо гистограмму).

4. Выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое тестопригодность?

2. Что такое наблюдаемость?

3. Что такое коэффициент передачи управляемости?

4. Что такое управляемость?

5. Как вычислить управляемость для синхронных или асинхронных схем?

6. Что такое наблюдаемость?

7. Как рассчитать тестопригодность узла схемы, всей схемы?

8. Как модифицировать схему для повышения тестопригодности?

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Р.Дж.Беннеттс. "Проектирование тестопригодных логических схем". М., Радио и Связь, 1990. 681.325.6.Б-463.