3. Расчет интенсивности отказов.

Среднее значение наработок изделий в партии до первого отказа называется средней наработкой до первого отказа. Этот термин применим как для ремонтируемых, так и для неремонтируемых изделий. Для неремонтируемых изделий вместо названного можно применять термин средняя наработка до отказа.

ГОСТом 13377 – 67 для неремонтируемых изделий введен еще один показатель надежности, называемый интенсивностью отказов.

Интенсивность отказов есть вероятность того, что неремонтируемое изделие, проработавшее безотказно до момента t, откажет в последующую единицу времени, если эта единица мала.

Интенсивность отказов изделия есть функция времени от его работы.

Задание :

- рассчитать интенсивность отказов λ(t) для заданных значений t и Δt.

- в предположении, что безотказность некоторого блока в электронной системе управления автомобиля характеризуется интенсивностью отказов, численно равной рассчитанной, причем эта интенсивность не меняется в течение всего срока его службы, необходимо определить наработку до отказа Т_Б такого блока.

Подсистема управления включает в себя k последовательно соединенных электронных блоков ( рис.2).

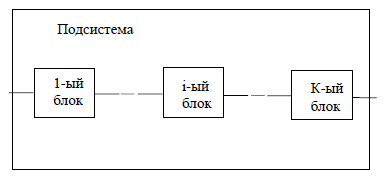
Рис.2 Подсистема управления с последовательно включенными блоками.

Эти блоки имеют одинаковую интенсивность отказов, численно равную рассчитанной. Требуется определить интенсивность отказов подсистемы λ_П и среднюю наработку ее до отказа , построить зависимости вероятности безотказной работы одного блока Р_Б(t) и подсистемы Р_П(t) от наработки и определить вероятности безотказной работы блока Р_Б(t) и подсистемы Р_П(t) к наработке t= T_П.

Интенсивность отказов λ(t) рассчитывается по формуле:

, (5)

Где - статистическая вероятность отказа устройства на интервале [t,t+Δt] или иначе статистическая вероятность попадания на указанный интервал случайной величины Т.

Р(t) – рассчитанная на шаге 1 – вероятность безотказной работы устройства.

Δt=3* 10³ч.

Заданное значение 10³ч - 6,5

Р(t) = 0,4

Интервал [t,t+Δt] = [6,5*10³ч ;9,5*10³ч]

= 20/50 = 0,4

λ(t) = 0,4 / 0,4*3*10³ч = 0,00033

Предположим, что интенсивность отказов не меняется в течение всего срока службы объекта, т.е. λ(t) = λ = const, то наработка до отказа распределена по экспоненциальному (показательному) закону.

В этом случае вероятность безотказной работы блока:

(6)

Р_Б(t) = exp (-0.00033*6.5*10³) = exp(-2.1666) = 0.1146

А средняя наработка блока до отказа находится как:

(7)

= 1/0,00033 = 3030,30 ч.

При последовательном соединении k блоков интенсивность отказов образуемой ими подсистемы:

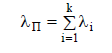(8)

Т.к.интенсивности отказов всех блоков одинаковы, то интенсивность отказов подсистемы:

(9)

λ_П = 4*0,00033 = 0,00132 ч.,

а вероятность безотказной работы системы:

(10)

Р_П(t) = exp (-0.00132*6.5*10³) = exp (-8,58) = 0.000188

С учетом (7) и (8) средняя наработка подсистемы до отказа находится как:

(11)

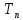= 1/0,00132 = 757,58 ч.

Вывод: по мере приближения к предельному состоянию – интенсивность отказов объектов возрастает.

4. Расчет вероятности безотказной работы.

Задание: Для наработки t = требуется рассчитать вероятность безотказной работы Рс() системы (рис. 3), состоящей из двух подсистем, одна из которых является резервной.

Рис. 3 Схема системы с резервированием.

Расчет ведется в предположении, что отказы каждой из двух подсистем независимы.

Вероятности безотказной работы каждой системы одинаковы и равны Р_П(). Тогда вероятность отказа одной подсистемы:

Q_П() = 1 – 0,000188 = 0,99812

Вероятность отказа всей системы определяется из условия, что отказала и первая, и вторая подсистемы, т.е.:

= 0,99812²= 0,99962

Отсюда вероятность безотказной работы системы:

,

Р_с(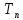) = 1 – 0,98 = 0,0037

Вывод: в данном задании была рассчитана вероятность безотказной работы системы при отказе первой и второй подсистемы. По сравнению с последова-тельной структурой вероятность безотказной работы системы меньше.