
2012 Формулы по Математической Статистике
.doc
Основные числовые характеристики выборки.
|
Негруппированная выборка |
Группированная выборка |
|
1.Среднее
арифметическое выборки (несмещённая
состоятельная оценка математического
ожидания
|
|
|
|
|
|
2.Дисперсия
выборки (смещённая состоятельная
оценка дисперсии
|
|
|
|
|
|
3.Исправленная
дисперсия
выборки (несмещённая состоятельная
оценка дисперсии
|
|
|
4.
Размах
выборки:
|
|
|
5.Мода
выборки: а)
|
|
|
6.Медиана
выборки: а)
б)
|
|
Доверительные
интервалы для параметров
![]() и
и
![]() нормального распределения.
нормального распределения.
|
Параметр |
Точечная оценка |
Доверительный интервал |
|
( |
|
|
|
( |
|
|
Доверительный
интервал для параметра
![]() биномиального распределения.
биномиального распределения.
|
Параметр |
Точечная оценка |
Доверительный интервал |
|
( |
|
|
Объём выборки
(повторной):
![]()
![]() или
или
![]() ;
;
![]()
Объём выборки
(бесповторной):

![]() или
или
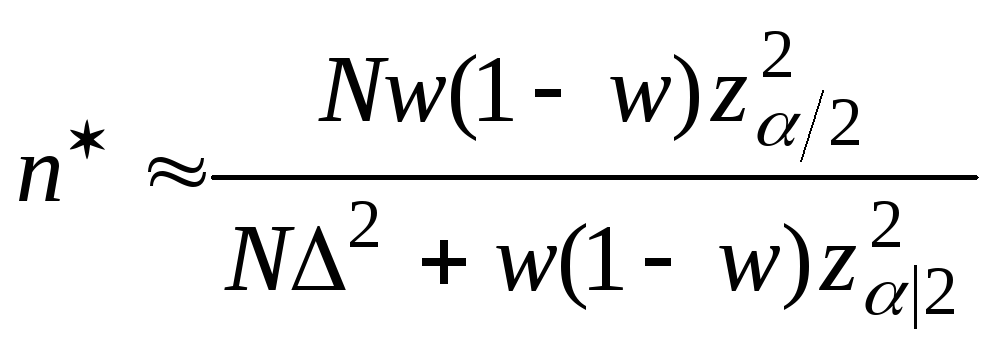 ,
где
,
где
![]() -объём
генеральной совокупности; если
-объём
генеральной совокупности; если
![]() -неизвестно,
то при определении объёма
-неизвестно,
то при определении объёма
![]() ,
,
![]() полагают
полагают
![]() .
.
Здесь:
![]() - корень уравнения
- корень уравнения
![]() (приложение
2);
(приложение
2);
![]() -критическая точка распределения
Стьюдента (приложение 4);
-критическая точка распределения
Стьюдента (приложение 4);
![]() ,
,
![]() -
критические точки распределения
-
критические точки распределения
![]() (приложение
3);
(приложение
3);
![]() -предельная
ошибка выборки;
-предельная
ошибка выборки;
![]() - доверительная вероятность;
- доверительная вероятность;
![]() -
число элементов в выборке, обладающих
данным свойством.
-
число элементов в выборке, обладающих
данным свойством.
Проверка гипотез о средних нормального распределения.
|
Гипотеза
|
Статистика критерия |
Критическое множество |
||
|
( |
|
|
||
|
|
|
|||
|
( |
|
|
||
|
|
|
|||
|
( |
|
|
||
|
|
|
|||
|
( |
|
|
||
|
|
|
|||
Здесь:
![]() - корень уравнения
- корень уравнения
![]() (приложение
2);
(приложение
2);
![]() - корень уравнения
- корень уравнения
![]() (приложение
2);
(приложение
2);
![]() ,
,![]() -критические точки распределения
Стьюдента для двусторонней и односторонней
критической области, соответственно
(приложение 4).
-критические точки распределения
Стьюдента для двусторонней и односторонней
критической области, соответственно
(приложение 4).
Проверка гипотез о дисперсиях нормального распределения.
|
Гипотеза
|
Статистика критерия |
Критическое множество |
|
|
( |
|
|
|
|
|
|
||
|
( |
|
|
|
|
|
|||
Здесь:
![]() ,
,
![]() ,
,![]() ,
,![]() -
критические точки распределения
-
критические точки распределения
![]() (приложение
3);
(приложение
3);
![]() ,
,
![]() -критические
точки распределения Фишера (приложение
5а,б).
-критические
точки распределения Фишера (приложение
5а,б).
Проверка гипотез
о параметре![]() биномиального
распределения
биномиального
распределения
|
Гипотеза
|
Статистика критерия |
Критическое множество |
||
|
|
|
|
||
|
|
|
|||
|
|
( |
|
||
|
|
|
|||
Здесь:
![]() - корень уравнения
- корень уравнения
![]() (приложение
2);
(приложение
2);
![]() - корень уравнения
- корень уравнения
![]() (приложение
2);
(приложение
2);
![]() ,
,
![]() -
число элементов в выборках объёма
-
число элементов в выборках объёма
![]() ,
,
![]() ,
соответственно, обладающих данным
свойством.
,
соответственно, обладающих данным
свойством.
Проверка гипотезы
о значимости выборочного коэффициента
корреляции
![]() .
.
|
Гипотеза
|
Статистика критерия |
Критическое множество |
|
|
|
|
Здесь:
![]() - критическая точка распределения
Стьюдента (приложение 4),
- критическая точка распределения
Стьюдента (приложение 4),
![]() -
объём выборки.
-
объём выборки.


 ,
где
,
где
 ,
,
 ,
,
 ,
,
 ,
где
,
где
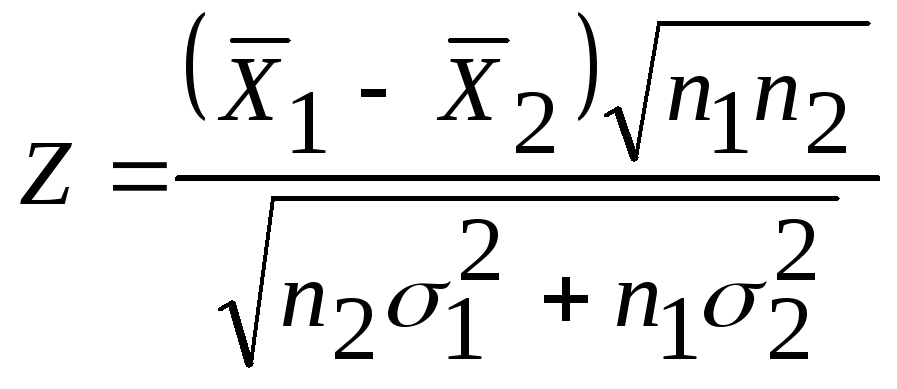
 где
где
 ,
где
,
где
 ,
где
,
где где
где