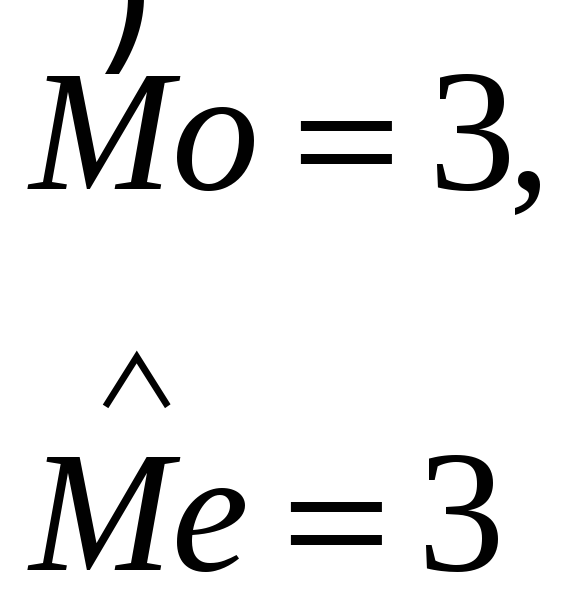2012_ТВиМС НУЛЕВОЙ ВАРИАНТ ЭКЗАМЕН-ТЕСТА
.doc
НУЛЕВОЙ ВАРИАНТ
экзаменационных тестов по дисциплине
«Теория вероятностей и математическая статистика»
|
№п/п |
Задания |
Ответы |
||||||||||||
|
Тема:
Комбинаторика: Правила суммы
и произведения комбинаторики;
комбинаторные числа
|
||||||||||||||
|
1. |
Количество различных трёхзначных
чисел не делящихся на
1)
|
1) |
||||||||||||
|
2. |
В новогоднем шахматном турнире участвуют 10 человек. Между любыми двумя участниками турнира должна быть сыграна одна партия. Тогда общее число партий, которое должно быть сыграно в турнире, равно: 1)
|
2) |
||||||||||||
|
3. |
Соответствие комбинаторного числа его значению: 1:
2:
3:
В ответе указать пары, соответствующих друг другу комбинаторных чисел и их значений. |
1-1 2-2 3-3 |
||||||||||||
|
4. |
В урне 5 чёрных и 6 белых шаров. Наудачу вынимают 4 шара. Тогда число способов отбора, при котором среди четырёх выбранных окажется два белых шара, равно: 1)
|
3) |
||||||||||||
|
Тема: Случайные события-1: Классическое определение. |
||||||||||||||
|
1. |
Наудачу выбрано двузначное число. Тогда вероятность того, что выбранное число простое (делится нацело только на единицу и на себя) и сумма его цифр – пять, равна: 1)
|
2) |
||||||||||||
|
2. |
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани кости появится менее трёх очков, равна: 1)
|
3) |
||||||||||||
|
3. |
Бросают три монеты. Тогда вероятность того, что «герб» появится хотя бы на одной монете, равна: 1)
|
5) |
||||||||||||
|
4. |
В урне два
белых, три чёрных и пять
красных шаров. Наудачу вынимают три
шара. Тогда вероятность того, что
все вынутые шары одного цвета,
равна
|
11/120 |
||||||||||||
|
Темы: Случайные события-2. Случайные события-3. Классическое определение, формулы сложения и умножения (открытая форма). Формула Бернулли, формулы полной вероятности и Байеса. |
||||||||||||||
|
1. |
Среди кандидатов в студсовет факультета
3 первокурсника, 5 второкурсников и 7
третьекурсников. Из этого состава
наудачу в студсовет выбирают 5 человек.
Тогда вероятность того, что среди
выбранных окажутся все три
первокурсника, равна
Вычисления
проводить в дробях. Ответ представить
в виде:
|
91 |
||||||||||||
|
2. |
Учитель
каждый день случайным образом отбирает
одного ученика для проверки подготовки
домашнего задания. Известно, что из
18 учеников 12 всегда полностью выполняют
домашнее задание. Тогда вероятность
того, что за шесть дней недели
учитель выставит четыре отрицательные
оценки равна
|
20 |
||||||||||||
|
3. |
Три станка-автомата производят
однотипную продукцию, поступающую на
сборочное производство в пропорции
Ответ
представить в виде несократимой дроби:
|
1/2 |
||||||||||||
|
4. |
В ящике
лежало три лотерейных билета, из них
один выигрышный. Один билет (неизвестно
какой) был утерян. Тогда вероятность
того, что билет, выбранный наудачу из
оставшихся билетов, окажется выигрышным
равна
|
1/3 |
||||||||||||
|
5. |
Имеются три одинаковых по виду ящика.
В первом ящике находятся 4 белых и 5
чёрных шаров, во втором – 5 белых и 4
чёрных, в третьем – 6 белых шаров. Из
наудачу выбранного ящика вынули белый
шар. Тогда вероятность того, что он
вынут из второго ящика, равна
Ответ представить
в виде:
|
18 |
||||||||||||
|
6. |
Результаты проверки выполнения контрольной работы по ТВ в двух студенческих группах показали, что в первой группе положительную оценку получили 20 студентов из 30, а во второй группе – 15 из 25. Наудачу выбранная работа имеет оценку «неудовлетворительно». Тогда вероятность того, что она написана студентом первой группы, равна: 1)
|
1) |
||||||||||||
|
7. |
Вероятность выиграть в шахматы у равносильного противника хотя бы одну из четырёх партий (ничьи во внимание не принимаются) равна: 1)
|
5) |
||||||||||||
|
8. |
Игральную
кость бросают
1)
|
2) |
||||||||||||
|
9 |
Вероятность попадания в цель при одном
выстреле
Ответ
представить в виде:
|
3 |
||||||||||||
|
Темы: Дискретные случайные величины-1. Непрерывные случайные величины-1. Случайные
величины-2. Ряд распределения
дискретной случайной величины. Функции
распределения
|
||||||||||||||
|
1. |
Известны дисперсии независимых
случайных величин
1)
|
2) |
||||||||||||
|
2. |
Известны математические
ожидания случайных величин
|
-7 |
||||||||||||
|
3. |
Дискретная случайная величина
1)
4)
|
3) |
||||||||||||
|
4. |
В партии из 6 деталей содержится 4
стандартных. Дискретная случайная
величина
Вычисления проводить
в дробях. Ответ представить в виде:
|
2 |
||||||||||||
|
5. |
Функция
распределения непрерывной случайной
величины
|
4 |
||||||||||||
|
Тема. Случайные величины-3: Основные законы распределения: биномиальный, равномерный, нормальный, показательный, их числовые характеристики. |
||||||||||||||
|
1. |
Случайная величина
Записать ответ. |
64 |
||||||||||||
|
2. |
Непрерывная случайная величина
равномерно распределена на отрезке
Вычисления проводить
в дробях. Ответ представить в виде:
|
2 |
||||||||||||
|
3. |
Вероятность того, что при трёх выстрелах
стрелок попадёт в цель хотя бы один
раз, равна
Вычисления
проводить в дробях. Ответ представить
в виде:
|
16 |
||||||||||||
|
4. |
Случайная величина
Вычисления
проводить в дробях. Ответ представить
в виде:
|
4 |
||||||||||||
|
Тема. Описательная статистика-1: Числовые характеристики выборки (среднее арифметическое, дисперсия, мода, медиана); графическое изображение выборки (полигон, гистограмма). |
||||||||||||||
|
1 |
При измерении
скорости ветра 26 сентября в течение
6 лет были получены значения:
1)
|
2) |
||||||||||||
|
2 |
Дано
статистическое распределение выборки
объёма
Тогда среднее арифметическое выборки
|
1)
|
||||||||||||
|
3 |
Дана выборка объёма
1)
|
1)
|
||||||||||||
|
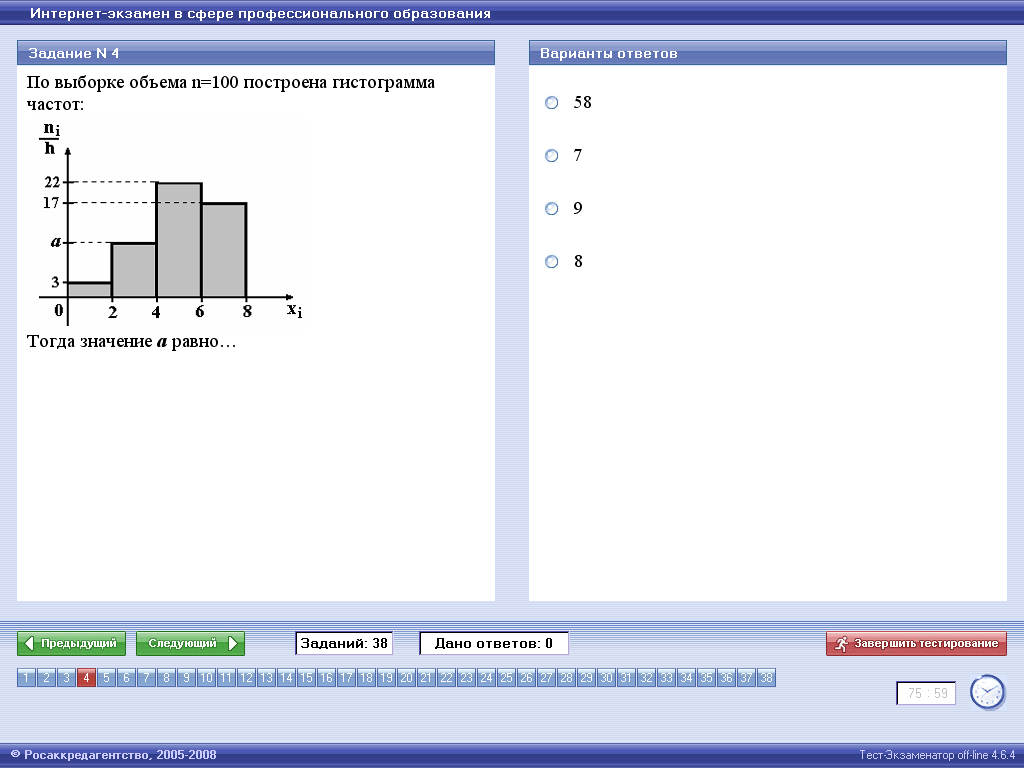
4 |
По выборке объема n=100 построена
гистограмма частот:
Тогда значение а равно:
1)
|
1) |
||||||||||||
|
5 |
Из генеральной совокупности извлечена
выборка объёма
Тогда число вариант
Записать ответ. |
|
||||||||||||

 .
Известно, что её дисперсия
.
Известно, что её дисперсия
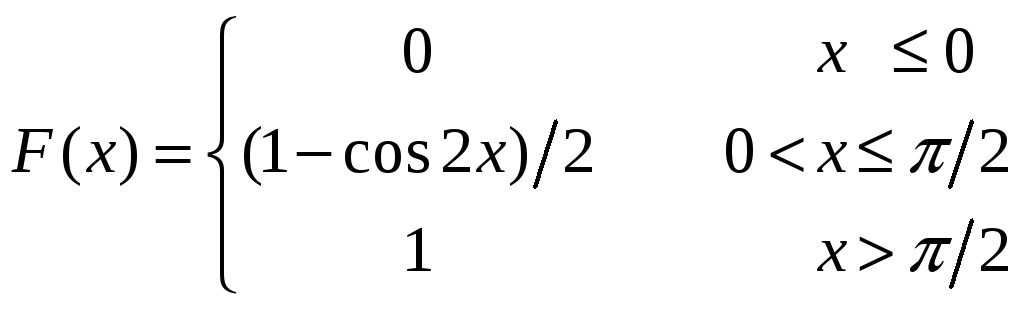 .
Тогда её математическое ожидание
.
Тогда её математическое ожидание
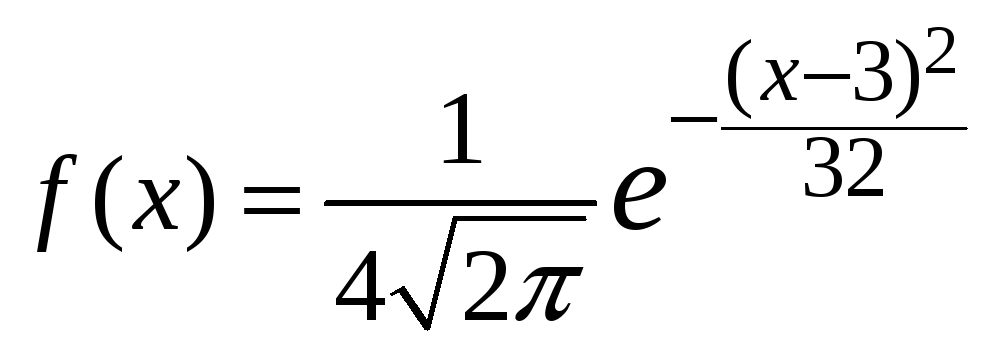 .
Тогда дисперсия
.
Тогда дисперсия
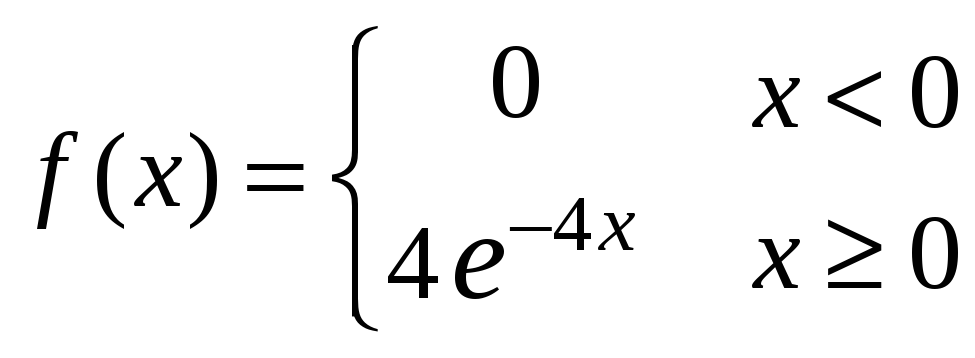 .
Тогда дисперсия
.
Тогда дисперсия