2. Алгоритм формирования случайной величины X, равномерно распределённой в диапазоне [a;b]

Рассматриваемый алгоритм генерирует дискретную случайную величину X, но шаг дискретности ∆Xможет быть настолько малым, что для практических задач моделированияXможет имитировать непрерывную случайную величину.

Вначале генерируется значение целой случайной величины R, равномерно распределённой в диапазоне [0;N–1].

В библиотеке функций языка программирования Cэто реализуется следующим образом:

R=random(N).

Значение Nнеобходимо выбирать достаточно большим (но не более допустимого максимального значения для заданного типа данных, например для целых беззнаковых 32767). При этом шаг дискретности ∆Xгенерируемой случайной величины будет равен

.

Случайная величина X, равномерно распределённая в диапазоне [a;b], вычисляется по формуле

,

где Z– переменная вещественного типа.

.

1.2.3 Алгоритм формирования случайной величины Yс нормальным законом распределения

Пусть при помощи алгоритма, описанного в п. 1.2.2. получено nнезависимых значений случайной величиныX, равномерно распределённых в диапазоне [–0.5; 0.5]. Обозначим их соответственноx₁,x₂,…x_n. Тогда суммируя по 6 значенийx_iполучим

,

где j=1,2,…m;k=6∙(j–1).

Случайная величина Xимеет нулевое среднее (M(x)=0), а дисперсия σ²_x=¹∕₁₂. ВеличинаYраспределена по закону, близкому к нормальному с математическим ожиданиемM(y)=0 и дисперсией σ²_x=0.5.

Напомним, что умножение Yна постоянный коэффициент C позволяет получить случайную величину, распределенную с дисперсией, равной 0.5∙C², а прибавлением кYпостоянной величины можно получить необходимое математическое ожидание.

1.2.4 Алгоритм формирования случайной величины с экспоненциальным законом распределения

Как известно, случайная величина , распределенная по экспоненциальныму закону описывается следующей плотностью распределения:

На рис. 1.1 построены графики экспоненциальных плотностей распределения при различных значениях параметра .

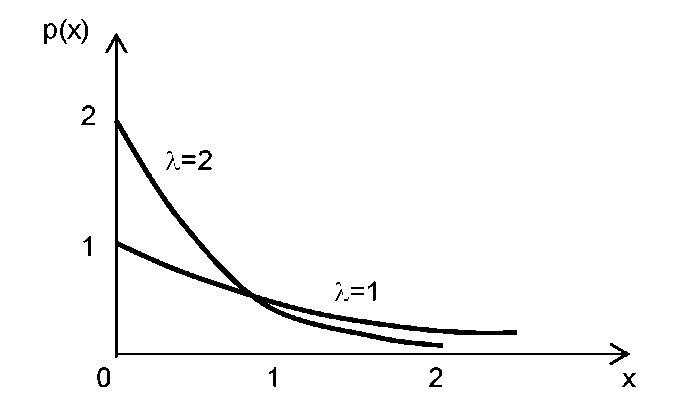
Рис. 1.1 Экспоненциальная плотность вероятностей с разными значениями параметра

Экспоненциальному распределению, как правило, подчиняется случайный интервал времени между поступлениями заявок в систему массового обслуживания. Поэтому весьма важно уметь моделировать потоки заявок разной интенсивности .

Математическое ожидание экспоненциально распределенной случайной величины равно:

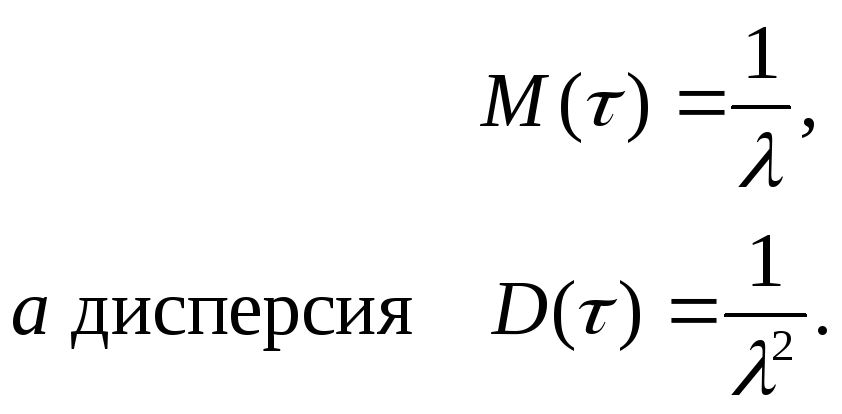
Чтобы найти алгоритм имитации экспоненциально распределенных чисел , пойдем от обратного. Приравняем равномерно распределенную на отрезке [0,1] величину R к интегралу от плотности распределения:

Взяв данный интеграл, получим:

откуда

но, поскольку случайная величина распределена точно так же, как , и находится в том же интервале , то предыдущую формулу можно заменить на более удобную:

что дает искомый ответ.