
- •Введение
- •1 Погрешность вычислений
- •2 Задача приближения функции
- •2.1 Задача интерполирования
- •2.2 Сплайн-интерполяция
- •3 Приближенное вычисление определенных интегралов
- •3.1 Метод прямоугольников
- •3.2 Метод трапеций
- •3.3 Метод парабол (метод Симпсона)
- •4 Приближенное вычисление линейных уравнений
- •4.1 Метод половинного деления
- •4.2 Метод касательных (метод Ньютона)
- •4.3 Метод хорд
- •4.5 Метод итераций
- •5 Решение задачи Коши
- •5.1 Метод Эйлера
- •5.2 Метод Рунге-Кутта
- •5.3 Метод степенных рядов
4 Приближенное вычисление линейных уравнений
Уравнением называется равенство двух функций f(x)=g(x).
Корнем уравнения называется значение независимой переменной, которое при подставлении его в исходное уравнение дает верное равенство.
Линейным
является уравнение вида:
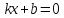 .
.
Приближенное решение линейных уравнений включает в себя следующие этапы:
Отделение корня
Отделение корня заключается в нахождении отрезка изоляции- отрезка, на оси OX, содержащего единственный корень данного уравнения.
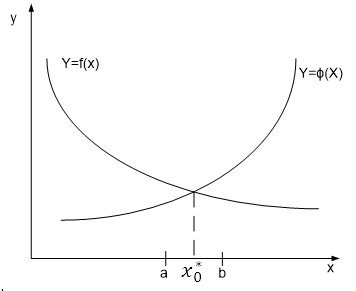
Удобнее всего данное действие выполнять графически:
Строятся
графики функций
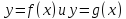 ,
затем находится абсцисса точки
пересечения
,
затем находится абсцисса точки
пересечения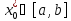 ,
где
,
где отрезок изоляции.
отрезок изоляции.
Или
же почленно перенести обе функции в
одну часть
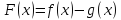 ,
и найти точку пересеченияF(x)
с осью OX,
т.е. точку
,
и найти точку пересеченияF(x)
с осью OX,
т.е. точку
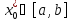 ,
где
,
где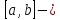 отрезок изоляции.
отрезок изоляции.
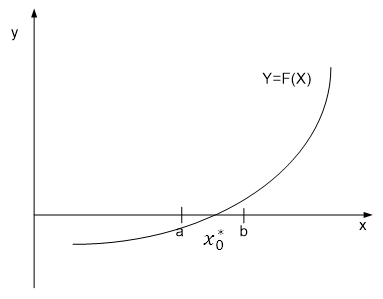
Проверка существования и единственности корня на отрезке изоляции
Если
F(x)
непрерывна на
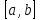 ,
то проверяются следующие условия:
,
то проверяются следующие условия:
Условие существования корня:
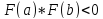 ;
;Условие единственности корня:
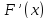 не меняет своего знака на
не меняет своего знака на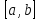 .
.
Уточнение корня
Уточнением корня называется вычисление значения корня с заданной точностью.
Существует несколько методов уточнения корня:
Метод половинного деления
Метод касательных (метод Ньютона)
Метод хорд
Комбинированный
Метод итераций
4.1 Метод половинного деления
Данный метод включает в себя следующие этапы:
Нахождение начального приближения:
Находим
точку с,
такую
что
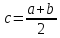 ,
где a
и
b
- крайние точки отрезка изоляции.
,
где a
и
b
- крайние точки отрезка изоляции.
Проверяем существование корня на отрезках
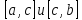 :
:
Если
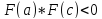 и
и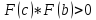 ,
то получаем новый отрезок изоляции
,
то получаем новый отрезок изоляции .
.Если
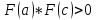 и
и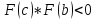 ,
то получаем новый отрезок изоляции
,
то получаем новый отрезок изоляции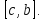
Допустим, мы получили отрезок изоляции
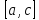 ,
тогда проверяем условие
,
тогда проверяем условие
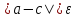 ,
где ε – допустимая погрешность. Если
данное условие выполняется, следовательно
,
где ε – допустимая погрешность. Если
данное условие выполняется, следовательно
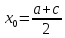 . В этом случае вычисления прекращаются.
. В этом случае вычисления прекращаются.
Если
условие
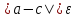 не выполняется, то вычисления продолжаются,
пока данное условие не будет выполнено.
не выполняется, то вычисления продолжаются,
пока данное условие не будет выполнено.
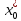
Достоинство данного метода заключается в простоте и в том, что он не требует дополнительных ограничений. Однако медленная сходимость данного метода является существенным недостатком.
4.2 Метод касательных (метод Ньютона)
Метод касательных заключается в том, что к графику функции F(x) в точке F(b) про водится касательная, при этом точка пересечения касательной с осью OX обозначается b1. Если условие проверки не выполняется, то проводится вторая касательная к графику в точке F(b1). Вычисления продолжаются пока не будет выполнено условие остановки счета:
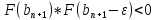 ,
где
,
где
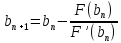
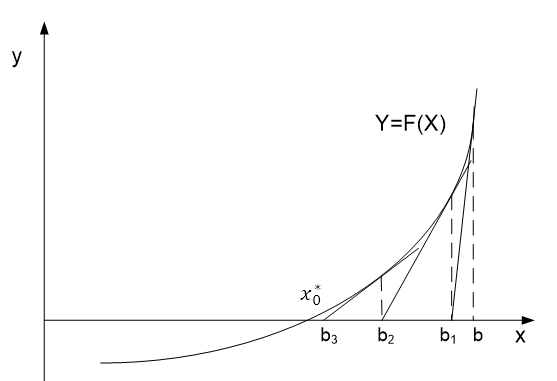
Достоинство этого метода заключаются в быстрой сходимости. Недостатками являются громоздкость вычислений и требование к отсутствию точек перегиба на отрезке изоляции.
Замечание: Касательная строится с того конца, где совпадают знаки второй производной и самой функции.
4.3 Метод хорд
Начальное приближение находится путем проведения хорды к графику функции F(x) от точки F(a) к точке F(b). При этом точка пересечения хорды с осью ОХ обозначается a1 и следующим приближением будет точка a2 -- точка пересечения оси ОХ хордой, проведенной из точки F(a1) к точке F(b).
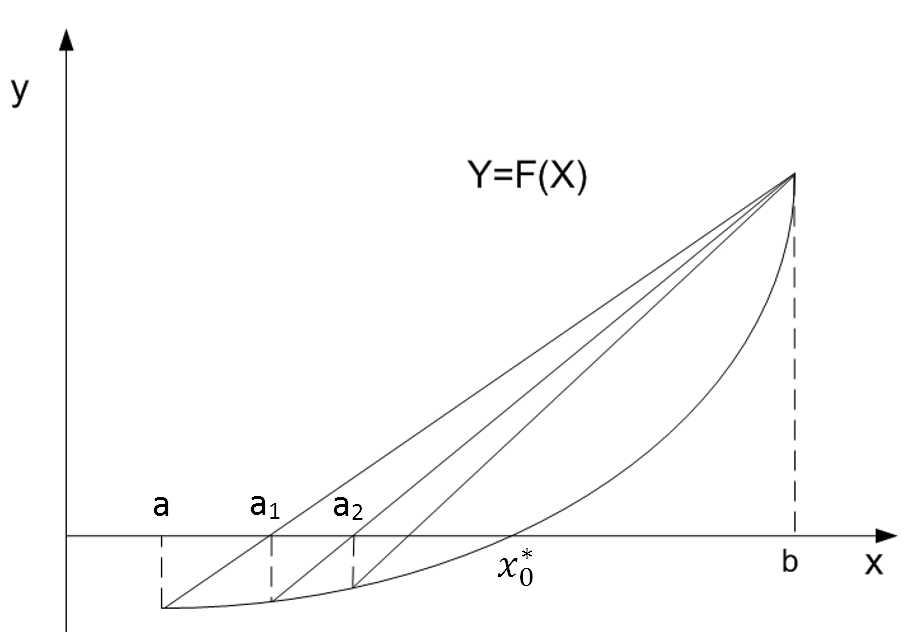
Если приближение слева:
 ;
;
Вычисления прекращаются при выполнении следующего условия:
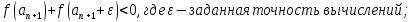
Если приближение справа:
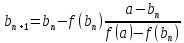 ;
;
Вычисления прекращаются при выполнении следующего условия:
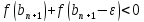 .
.
Достоинства и недостатки этого метода аналогичны достоинствам и недостаткам метода касательных.
Так же часто применяют комбинированный метод, где осуществляют приближение поочередно методами касательных и хорд – то есть приближение происходит с двух сторон от искомой точки.
