Дифференциал функции

Можно доказать, что если функция имеет при некоторой базе предел, равный конечному числу, то ее можно представить в виде суммы этого числа и бесконечно малой величины при той же базе (и наоборот): .

Применим это теорему к дифференцируемой функции: .

Отсюда .

Таким образом, приращение функции у состоит из двух слагаемых: 1) линейного относительнох, т.е.f`(x)х; 2) нелинейного относительнох, т.е.(x)х. При этом, так как, это второе слагаемое представляет собой бесконечно малую более высокого порядка, чемх.

Дифференциаломфункции называется главная, линейная относительнох часть приращения функции, равная произведению производной на приращение независимой переменнойdy=f`(x)х.

Найдем дифференциал функции у = х.

Так как dy=f`(x)х =x`х =х, тоdx=х, т.е. дифференциал независимой переменной равен приращению этой переменной.

Поэтому формулу для дифференциала функции можно записать в виде dy=f`(x)dх. Именно поэтому одно из обозначений производной представляет собой дробьdy/dх.

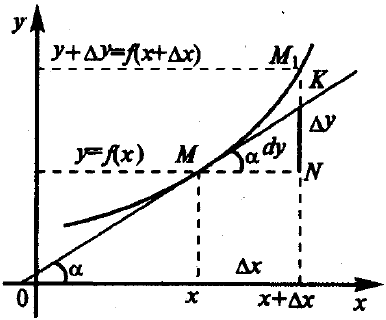
Геометрический смысл дифференциала проиллюстрирован рисунком 3.11. Возьмем на графике функции y = f(x) произвольную точку М(х, у). Дадим аргументу х приращение х. Тогда функция y = f(x) получит приращениеy = f(x +х) - f(x). Проведем касательную к графику функции в точке М, которая образует уголс положительным направлением оси абсцисс, т.е.f`(x) = tg. Из прямоугольного треугольника MKNKN=MN*tg=х*tg=f`(x)х =dy.

Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда х получает приращение х.

Свойства дифференциалав основном аналогичны свойствам производной:

1. dc = 0.

2. d(cu)=cdu.

3. d(u ± v) = du ± dv.

4. d(uv) = v du + u dv.

5. d(u/v) = (v du - u dv)/v².

Однако, существует важное свойство дифференциала функции, которым не обладает ее производная – это инвариантность формы дифференциала.

Из определения дифференциала для функции y= f(x) дифференциалdy=f`(x)dх. Если эта функцияyявляется сложной, т.е.y= f(u), гдеu=(х), тоy= f[(х)] иf`(x) = f `(u)*u`. Тогдаdy= f `(u)*u`dх. Но для функцииu=(х) дифференциалdu=u`dх. Отсюдаdy= f `(u)*du.

Сравнивая между собой равенства dy=f`(x)dх иdy= f `(u)*du, убедимся, что формула дифференциала не изменяется, если вместо функции от независимой переменной х рассматривать функцию от зависимой переменнойu. Это свойство дифференциала и получило название инвариантности (т.е. неизменности) формы (или формулы) дифференциала.

Однако в этих двух формулах все же есть различие: в первой из них дифференциал независимой переменной равен приращению этой переменной, т.е. dx = x, а во в торой дифференциал функции du есть лишь линейная часть приращения этой функцииuи только при малыхх duu.

Применение дифференциала в приближенных вычислениях

Выше было показано, что , т.е. приращение функцииу отличается от ее дифференциала dy на бесконечно малую величину более высокого порядка, чемх.

Поэтому при достаточно малых значениях хуdy или f(x +х) - f(x)f`(x)х, откуда f(x +х)f(x) +f`(x)х. Полученная формула будет тем точнее, чем меньшех.

Например, найдем

Итак, y=f(x) =x^1/3. Возьмемx= 125,х = 0,27.

f `(x) = (x<sup>1/3</sup>)`= 1/(3x^2/3)

f(125,27) = f(125 + 0,27)  f(125) + f `(125)*(0,27) = = 5 + 0,27/(3*25) = 5,0036

Например, найдем tg 46^о.

Итак, y=f(x) =tgx. Возьмемx= 45^o=/4,х = 1^o =/180.

f`(x) = (tgx)`= 1/cos²x

f(46^o) = f(/4 + /180)  f(/4) + f `(/4)*(/180) = tg(/4) + + (1/ cos²(/4))*(/180) = 1 + (1/(2/2)²)*(/180) = 1 + /90 ( 1,035)

Кроме того, с помощью дифференциала может быть решена задача определения абсолютной и относительной погрешностей функции по заданной погрешности нахождения (измерения) аргумента.

Пусть необходимо вычислить значение данной функции у = f(x) при некотором значении аргумента х₁, истинная величина которого неизвестна, а известно лишь его приближенное значение х с абсолютной погрешностью |х| = |х - х₁|. Если вместо истинного значенияf(x₁) взять величинуf(x), то абсолютная ошибка функции будет равна |f(x₁) -f(x)| = |y|dy=f`(x)х.

При этом относительная погрешность функции _y= |y/y| при достаточно малыхх будет равна, где Е_х(y) – эластичность функции, а_х= |x/x| - относительная погрешность аргумента.