Выпуклость функции многих переменных

Функция f(X), заданная в выпуклой области, называется выпуклой вниз(вверх), если для любых точек Х⁽¹⁾, Х⁽²⁾из области ее определения и любого числа 01 выполняется:

f(X⁽¹⁾ + (1-)Х⁽²⁾)()f(X⁽¹⁾) + (1-)f(Х⁽²⁾)

Для функции одной переменной это означает, что выпуклая вверх функция лежит выше отрезка, соединяющего любые две точке ее графика, а выпуклая вниз – ниже.

Определение выпуклой функции уже давалось ранее при изучении исследования функций с помощью дифференциального счисления, только вместо формулы отрезка использовалась формула, определяющая середину отрезка (см. рисунок 3.7).

Если неравенства в определении выполняются, как строгие, то функция называется строго выпуклой. В соответствии с этим определением линейная функция является нестрого выпуклой одновременно вверх и вниз.

Для выпуклой функции равенство нулю частных производных является не только необходимым, но и достаточным условием экстремума. Т.е. если функция является строго выпуклой на всей рассматриваемой области, и получена стационарная точка, то в ней достигается глобальный максимум (при выпуклости вверх) или минимум (при выпуклости вниз).

Для отыскания глобального максимума (наибольшего значения) выпуклой вниз функции или глобального минимума (наименьшего значения) выпуклой вверх функции достаточно исследования экстремумов только на границе области определения.

Условный экстремум

Рассмотренные выше ситуации поиска локальных и глобальных экстремумов представляли собой задачи нахождения безусловных экстремумов, или задачибезусловной оптимизации. Если на аргументы функции наложены некоторые дополнительные ограничениями в форме равенств, то задача оптимизации превращается взадачу на условный экстремум.

Такую задачу можно записать в общем виде следующим образом:

или,

где Х=(х₁, х₂, . . . х_n), а выраженияg_i(X) =bⁱназываютуравнениями связи,m– число таких уравнений (записьозначает, что система имеет вид).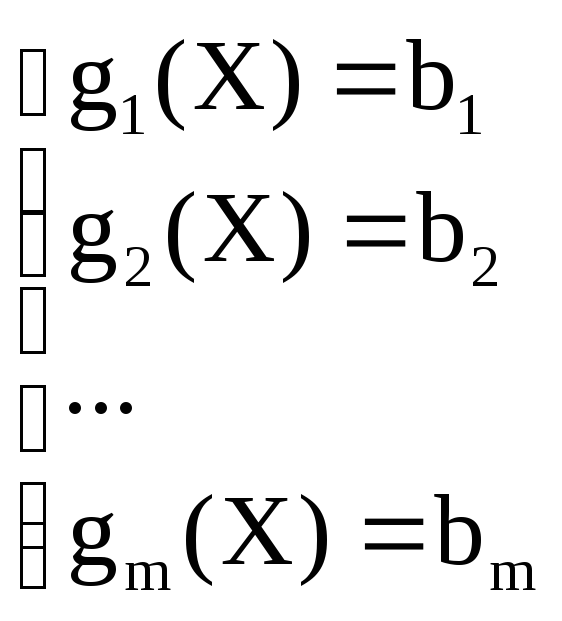

Если есть возможность выразить из ограничений задачи mпеременных через (n-m) остальных, то тривиальным подходом к решению является подстановка этих переменных в целевую функцию и далее безусловная оптимизация полученной функции.

Если такой возможности нет, то для нахождения условного экстремума в математическом анализе используют метод множителей Лагранжа. Он состоит в том, что строитсяфункция Лагранжа, имеющая следующий вид:

L(x₁, . . ., x_n, ₁, . . ., _m) = f(x₁, . . ., x_n) + _i (b_i - g_i(x₁, . . ., x_n)),

где _i,-множители Лагранжа.

Можно доказать, что если задача на условный экстремум имеет решение в некоторой точке, то существуют такие значения множителей Лагранжа, что вместе с координатами этой точки они будут представлять собой точку экстремума функции Лагранжа. Поэтому для решения задачи достаточно провести исследование на экстремум функции Лагранжа.

Приближенные методы оптимизации

Общего точного сходящегося метода решения задач оптимизации не существует. Однако, существуют общие приближенные методы.

Наиболее известны так называемые методы спуска. В общем случае они обеспечивают получение оптимального решения (если оно существует) через бесконечный процесс последовательных приближений. Однако, иногда процесс может закончиться получением точного решения и за конечное число шагов.

Суть методов заключается в том, что начиная с некоторой точки, осуществляют последовательный переход к некоторым другим точкам до тех пор, пока не выявится приемлемое решение задачи (см. рисунок 5.10). Решение будет приемлемым, если либо получен точный результат (по некоторому признаку), либо на последней итерации была достигнута заданная точность вычислений (например, функция возросла или уменьшилась не более чем на некоторую малую величину).

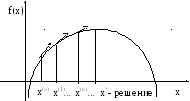
Рисунок 5.10 – Метод спуска

Кроме того, в общем случае методы спуска приводят лишь к локальному, а не к глобальному экстремуму. Поэтому они оказываются более эффективными при решении задач с выпуклыми функциями, в которых любой локальный экстремум является одновременно и глобальным.

Свое название методы спуска получили благодаря тому, что в большинстве учебников по оптимизации рассматриваются задачи на минимум (соответственно, поиск экстремума будет представлять собой не «подъем», как на рисунке 5.10, а «спуск»).

В зависимости от того, какая информация используется в алгоритме методов спуска, их подразделяют на:

1) методы нулевого порядка - используют только информацию о значениях самих функций;

2) методы первого порядка - используют, кроме того, информацию о значениях первых производных;

3) методы второго порядка - используют информацию о вторых производных.

Чаще всего при выборе способа перехода к последующим точкам рассчитывается градиент функции в очередной точке (поскольку именно он показывает направление наискорейшего роста функции). Такие методы называют градиентными методами.