Градиент функции

Из школьного курса математики известно, что вектор на плоскости представляет собой направленный отрезок. Его начало и конец имеют по две координаты. Координаты вектора рассчитываются путем вычитания из координат конца координат начала.

Понятие вектора может быть распространено и на n-мерное пространство (вместо двух координат будетnкоординат).

Градиентомgradzфункцииz=f(х₁, х₂, …х_n) называется вектор частных производных функции в точке, т.е. вектор с координатами.

Можно доказать, что градиент функции характеризует направление наискорейшего роста уровня функции в точке.

Например, для функции z= 2х₁ + х₂(см. рисунок 5.8) градиент в любой точке будет иметь координаты (2; 1). Построить его на плоскости можно различными способами, взяв в качестве начала вектора любую точку. Например, можно соединить точку (0; 0) с точкой (2; 1), или точку (1; 0) с точкой (3; 1), или точку (0; 3) с точкой (2; 4), или т.п. (см. рисунок 5.8). Все построенные таким образом вектора будут иметь координаты (2 – 0; 1 – 0) = = (3 – 1; 1 – 0) = (2 – 0; 4 – 3) = (2; 1).

Из рисунка 5.8 хорошо видно, что уровень функции растет в направлении градиента, поскольку построенные линии уровня соответствуют значениям уровня 4 > 3 > 2.

Рисунок 5.8 - Градиент функции z= 2х₁ + х₂

Рассмотрим другой пример – функцию z= 1/(х₁х₂). Градиент этой функции уже не будет всегда одинаковым в разных точках, поскольку его координаты определяются формулами (-1/(х₁²х₂); -1/(х₁х₂²)).

На рисунке 5.9 представлены линии уровня функцииz= 1/(х₁х₂) для уровней 2 и 10 (прямая 1/(х₁х₂) = 2 обозначена пунктиром, а прямая 1/(х₁х₂) = 10 – сплошной линией).

Рисунок 5.9 - Градиенты функции z= 1/(х₁х₂) в различных точках

Возьмем, например, точку (0,5; 1) и вычислим градиент в этой точке: (-1/(0,5²*1); -1/(0,5*1²)) = (-4; -2). Заметим, что точка (0,5; 1) лежит на линии уровня 1/(х₁х₂) = 2, ибоz=f(0,5; 1) = 1/(0,5*1) = 2. Чтобы изобразить вектор (-4; -2) на рисунке 5.9, соединим точку (0,5; 1) с точкой (-3,5; -1), ибо (-3,5 – 0,5; -1 - 1) = (-4; -2).

Возьмем другую точку на той же самой линии уровня, например, точку (1; 0,5) (z=f(1; 0,5) = 1/(0,5*1) = 2). Вычислим градиент в этой точке (-1/(1²*0,5); -1/(1*0,5²)) = (-2; -4). Чтобы изобразить его на рисунке 5.9, соединим точку (1; 0,5) с точкой (-1; -3,5), ибо (-1 - 1; -3,5 - 0,5) = (-2; -4).

Возьмем еще одну точку на той же самой линии уровня, но только теперь в неположительной координатной четверти. Например, точку (-0,5; -1) (z=f(-0,5; -1) = 1/((-1)*(-0,5)) = 2). Градиент в этой точке будет равен (-1/((-0,5)²*(-1)); -1/((-0,5)*(-1)²)) = (4; 2). Изобразим его на рисунке 5.9, соединив точку (-0,5; -1) с точкой (3,5; 1), ибо (3,5 – (-0,5); 1 – (-1)) = (4; 2).

Следует обратить внимание, что во всех трех рассмотренных случаях градиент показывает направление роста уровня функции (в сторону линии уровня 1/(х₁х₂) = 10 > 2).

Можно доказать, что градиент всегда перпендикулярен линии уровня (поверхности уровня), проходящей через данную точку.

Экстремумы функции многих переменных

Определим понятие экстремумадля функции многих переменных.

Функция многих переменных f(X) имеет в точке Х⁽⁰⁾максимум (минимум),если найдется такая окрестность этой точки, что для всех точек Х из этой окрестности выполняются неравенстваf(X)f(X⁽⁰⁾) ().

Если эти неравенства выполняются, как строгие, то экстремум называется сильным, а если нет, тослабым.

Заметим, что определенный таким образом экстремум носит локальныйхарактер, так как эти неравенства выполняются лишь для некоторой окрестности точки экстремума.

Необходимым условием локального экстремума дифференцируемой функции z=f(х₁, . . ., х_n) в точке является равенство нулю всех частных производных первого порядка в этой точке: .

Точки, в которых выполняются эти равенства, называются стационарными.

По-другому необходимое условие экстремума можно сформулировать так: в точке экстремума градиент равен нулю. Можно доказать и более общее утверждение - в точке экстремума обращаются в ноль производные функции по всем направлениям.

Стационарные точки должны быть подвергнуты дополнительным исследованиям - выполняются ли достаточные условия существования локального экстремума. Для этого определяют знак дифференциала второго порядка. Если при любых , не равных одновременно нулю, он всегда отрицателен (положителен), то функция имеет максимум (минимум). Если может обращаться в ноль не только при нулевых приращениях, то вопрос об экстремуме остается открытым. Если может принимать как положительные, так и отрицательные значения, то экстремума в стационарной точке нет.

В общем случае определение знака дифференциала представляет собой достаточно сложную проблему, которую здесь рассматривать не будем. Для функции двух переменных можно доказать, что если в стационарной точке, то экстремум присутствует. При этом знак второго дифференциала совпадает со знаком, т.е. если, то это максимум, а если, то это минимум. Если, то экстремума в этой точке нет, а если, то вопрос об экстремуме остается открытым.

Пример 1. Найти экстремумы функции.

Найдем частные производные методом логарифмического дифференцирования.

ln z = ln 2 + ln (x + y) + ln (1 + xy) – ln (1 + x²) – ln (1 + y²)

Аналогично.

Найдем стационарные точки из системы уравнений:

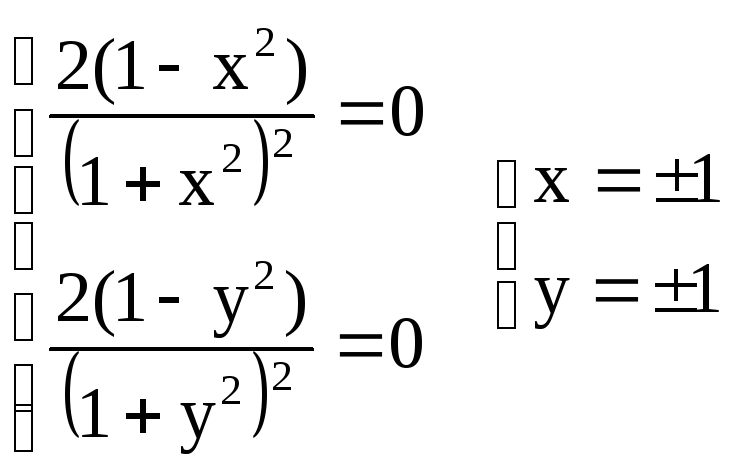
Таким образом, найдены четыре стационарные точки (1; 1), (1; -1), (-1; 1) и (-1; -1).

Найдем частные производные второго порядка:

ln (z _x `) = ln 2 + ln (1 - x²) -2ln (1 + x²)

Аналогично;.

Так как , знак выражениязависит только от. Отметим, что в обеих этих производных знаменатель всегда положителен, поэтому можно рассматривать только знак числителя,или даже знак выражений х(х²– 3)иy(y²– 3). Определим его в каждой критической точке и проверим выполнение достаточного условия экстремума.

Для точки (1; 1) получим 1*(1²– 3) = -2 < 0. Т.к. произведение двух отрицательных чисел> 0, а< 0, в точке (1; 1) можно найти максимум. Он равен= 2*(1 + 1)*(1 +1*1)/((1 +1²)*(1 +1²)) = = 8/4 = 2.

Для точки (1; -1) получим 1*(1²– 3) = -2 < 0 и (-1)*((-1)²– 3) = 2 > 0. Т.к. произведение этих чисел< 0, в этой точке экстремума нет. Аналогично можно показать, что нет экстремума в точке (-1; 1).

Для точки (-1; -1) получим (-1)*((-1)²– 3) = 2 > 0. Т.к. произведение двух положительных чисел> 0, а> 0, в точке (-1; -1) можно найти минимум. Он равен 2*((-1) + (-1))*(1 +(-1)*(-1))/((1 +(-1)²)*(1 +(-1)²)) = -8/4 = = -2.

Найти глобальныймаксимум или минимум (наибольшее или наименьшее значение функции) несколько сложнее, чем локальный экстремум, так как эти значения могут достигаться не только в стационарных точках, но и на границе области определения. Исследовать поведение функции на границе этой области не всегда легко.