

Московский государственный технический
УНИВЕРСИТЕТ «МАМИ»
Кафедра физики
ЛАБОРАТОРНАЯ РАБОТА 3.03
Изучение интерференции света при наблюдении колец Ньютона.
Москва 2005 г.
1
ЛАБОРАТОРНАЯ РАБОТА 3.03
Изучение интерференции света при наблюдении колец Ньютона.
Цель работы:Определение радиуса кривизны стеклянной линзы и длины световой волны; определение разности хода (разности фаз) интерферирующих волн.
Теоретическое введение
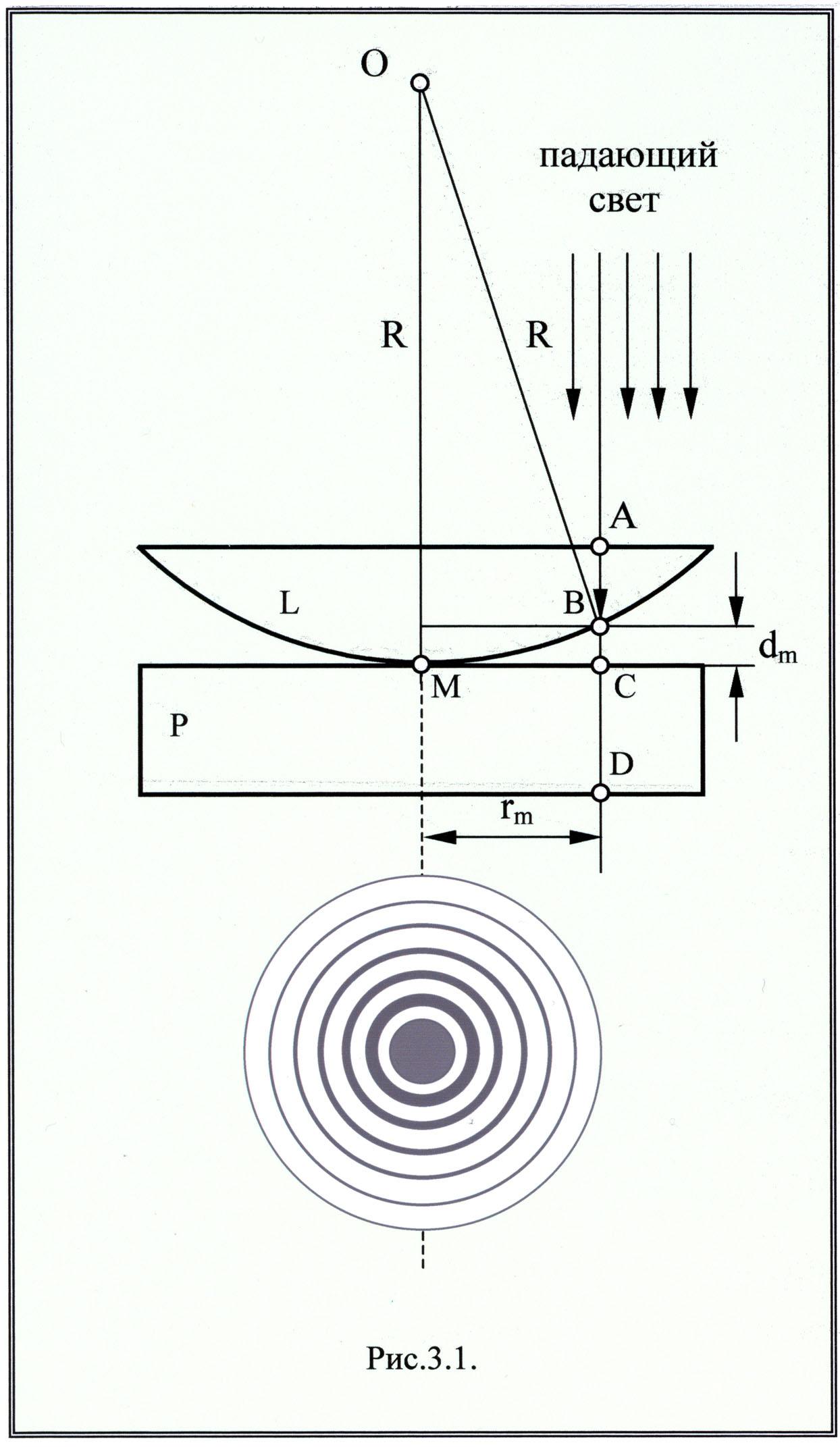
В данной лабораторной работе изучают интерференционную картину, носящую название к о л ь ц а Н ь ю т о н а. Так как контрастная интерференционная картина возникает обычно в отражённом свете, то устройство для наблюдения колец Ньютона осуществляется с учетом этого обстоятельства. Пусть плоская световая
волна падает на систему, сос-
тоящую из стеклянной линзы
и стеклянной пластины, как это показано на рис. 3.1. Плоско-выпуклая линза L большого радиуса кривизны накладывает-ся выпуклой стороной на плоскую стеклянную пластину Р. Между соприкасающимися в точке М поверхностями линзы L и пластины Р образуется воздушный клинообразный слой. Отражение световых волн происходит в точках А, В, С и D. Однако достаточно малую протяженность имеет лишь отрезок ВС (длина отрезка l меньше lког.), поэтому когерентными можно считать лишь волны, отраженные от нижней поверхности линзы (точка В) и верхней поверхности пластины (точка С). В точке В световой луч разделяется на два (рис. 3.2). Один луч отражается от выпуклой поверхности линзы (луч 1), другой (луч 2) преломляется, проходит воздушный зазор между линзой и пластиной и, отразившись от верхней поверхности пластины в точке С, возвращается обрат
2
но.
Полученные таким образом два когерентных
луча 1 и 2 дают интерференционный эффект
вблизи выпуклой поверхности линзы в
точке B.
Как уже отмечалось выше, для получения
интерференционной картины используется
линза с достаточно большим радиусом
кривизны. В этом случае клиновидный
воздушный зазор будет иметь очень малый
угол. Если еще
учесть, что и углы падения в этом случае
также будут достаточно малы, то тогда
точка наложения лучей Вбудет близка к точке В и практически
б удет
находиться на выпуклой поверхности
линзы. Следовательно, если при вычислении
оптической разности хода волн пренебречь
небольшими неизбежными наклонами лучей,
происходящих в тонком воздушном зазоре,
то оптическая разность хода волн,
отраженных в точках В и С и интерферирующих
в отраженном свете, определяется, как
видно из рис. 3.2, соотношением
удет
находиться на выпуклой поверхности
линзы. Следовательно, если при вычислении
оптической разности хода волн пренебречь
небольшими неизбежными наклонами лучей,
происходящих в тонком воздушном зазоре,
то оптическая разность хода волн,
отраженных в точках В и С и интерферирующих
в отраженном свете, определяется, как
видно из рис. 3.2, соотношением
![]() ,
(3.1)
,
(3.1)
где
d
- толщина зазора между пластиной Р
и линзой L
; n
показатель преломления среды, заполняющий
пространство между ними ;
- длина волны падающего света. Слагаемое
/2
учитывает изменение фазы световой
волны на
при отражении от стеклянной пластины
в точке С,
так как стекло является оптически более
плотной средой, чем воздух, что эквивалентно
уменьшению пути на /2.
Пространство между линзой и пластиной
заполнено в нашем случае воздухом
![]() ,
поэтому разность хода интерферирующих
волн составляет
,
поэтому разность хода интерферирующих
волн составляет
![]() .
(3.2)
.
(3.2)
В соответствии с (3.2) разность хода при заданном значении длины волны в данном эксперименте определяется только толщиной воздушного зазора, поэтому разность хода будет одинакова для всех волн, отраженных на одинаковом расстоянии от геометрического центра системы (точки соприкосновения М линзы и пластины). Вследствие этого интерференционная картина имеет вид концентрических колец. В центре картины, где d = 0, наблюдают темное кольцо, что соответствует разности хода отраженных волн /2. (Вид колец Ньютона показан на рис. 3.1, внизу).
Связь между радиусом интерференционного кольца r, радиусом R кривизны линзы и длиной световой волны может быть найдена с использованием простых геометрических соображений. Для этого снова обратимся к рис. 3.1. Здесь R радиус кривизны выпуклой поверхности линзы, rm радиус интерференционного кольца, имеющего порядок интерференции m , где dm толщина воздушного слоя в
3
том
месте, где наблюдается интерференционная
полоса с радиусом
![]() .
Из рис. 3.1 имеем
.
Из рис. 3.1 имеем
![]() .
(3.3)
.
(3.3)
Отсюда,
принимая во внимания, что
![]() ,
получим
,
получим
![]() .
(3.4)
.
(3.4)
Подставив полученное выражение в соотношение (3.2), получим
![]() .
(3.5)
.
(3.5)
Запишем условие минимума освещенности в интерференционной картине
![]() ,
,
![]() (3.6)
(3.6)
Принимая во внимание (3.5) , получим выражение для радиусов темных колец
![]() .
(3.7)
.
(3.7)
Отсюда, измерив rm и зная m и R , можно определить длину волны света , или, наоборот , по известному значению λ найти R .
Однако,
практически очень трудно добиться
идеального контакта сферической
поверхности линзы и плоской пластины
в одной точке вследствие упругой
деформации стекла и попадания в место
соприкосновения пылинок. Поэтому
непосредственно использовать формулу
(3.7) для вычислений нельзя: m
ому темному
кольцу в действительности может
соответствовать не
m
ный порядок
интерференции,
а
![]() ,где
p
неизвестное
число, одинаковое для всех колец.
,где
p
неизвестное
число, одинаковое для всех колец.
Для
исключения возможной ошибки расчет
длины волны
производят
по разности
квадратов колец
![]() и
и![]() .
В этом случае неизвестное p
исключается, и
.
В этом случае неизвестное p
исключается, и![]() расчетная
формула принимает вид:
расчетная
формула принимает вид:
![]() .
(3.8)
.
(3.8)
