Лабораторная работа №2.

Быстрое преобразование Фурье. Дискретная свертка.

Краткое описание.

В этой работе будет рассмотрен и исследован алгоритм БПФ, будет оценена его производительность, также я приведу сравнительный анализ моей реализации с реализацией в среде MATLAB.

Во второй части работы мы сравним различные реализации дискретной свёртки и выясним, какие из них когда лучше использовать. Также проведём сравнительный анализ с функцией conv среды MATLAB.

Итак, теперь по пунктам:

1. Реализовать на С или С++ алгоритмы непосредственного вычисления ДПФ и ОДПФ по формулам (1) и (2) для комплексного входного сигнала с двойной точностью (double).

Во-первых, все мои реализации алгоритмов написаны на C и находятся в каталоге fft, там же лежит тестовый проект fft.vcproj для Visual Studio 2008 и batch файлы:

make_conv.bat

make_dft.bat

make_fastconv.bat

make_fft.bat

make_idft.bat

make_ifft.bat

которые собирают MEX модули для MATLAB’а, каждый модуль содержит одну реализацию определённого алгоритма, а именно:

make_conv.bat – алгоритм свёртки по формуле (7)

make_dft.bat – алгоритм ДПФ по формуле (1)

make_fastconv.bat – алгоритм свёртки с использованием БПФ

make_fft.bat – алгоритм БПФ

make_idft.bat – алгоритм ОДПФ по формуле (2)

make_ifft.bat – алгоритм ОБПФ

при компиляции генерируются следующие модули:

labconv.mexw32

labdft.mexw32

labfastconv.mexw32

labfft.mexw32

labidft.mexw32

labifft.mexw32

теперь эти функции можно вызывать из MATLAB вот так:

Z = labconv(X, Y);

Y = labfft(X);

и т.д.

При реализации алгоритмов я старался как можно лучше оптимизировать их, так чтобы производительность их была предельной возможной (для языка C, естественно, написав те же самые алгоритмы на ассемблере можно получить куда более лучшие результаты ), в этом отчёте я в вкратце поясню их работу.

Что касается реализаций ДПФ и ОДПФ, то описывать особо нечего, можно лишь упомянуть о вспомогательной функции BitCount, которая используется в реализации ДПФ и ОДПФ (да и много где ещё) для быстрого подсчёта к-ва единичных битов в 32-битном числе, на основании этого можно сделать вывод является число степенью двойки или нет, если к-во единичных битов в числе == 1, то это число является степенью двойки, в противном случае – нет. Функция BitCount реализует алгоритм “MIT Hackmem”.

2. Реализовать на С или С++ алгоритмы прямого и обратного БПФ для комплексного входного сигнала длиной 2^n , n – любое натуральное число с прореживанием по времени и двоично-инверсными перестановками

Здесь первым делом производятся двоично-инверсные перестановки, делается это следующим образом:

1. берётся число

2. к текущему числу прибавляется инверсная единица (например для 3-x разрядного числа инверсная единица это 100₂)

3. если произошло переполнение, то берём инверсную единицу для количества разрядов меньшего текущего на один и переходим к шагу 2

4. Выполняем до тех пор, пока переполнения в результате сложения не произойдёт.

Таким образом мы можем сгенерировать нужную последовательность.

Пример для 3-х разрядов:

Т.е наши начальные числа: 0 1 2 3 4 5 6 7

Берём 000₂, прибавляем 100₂, получаем 100₂. Переполнения не произошло, первое число получено – 4, далее, берём полученное число – 4 - 100₂ и прибавляем 100₂, получаем 000₂ и переполнение, следовательно добавляем ещё 10₂ и получаем 010₂ = 2 и т.д, в итоге получим последовательность 0 4 2 6 1 5 3 7 – то что нужно и очень быстро.

Далее начинает работу сам алгоритм БПФ по формулам с тремя вложенными циклами, стоит также заметить, что омега не считается, все омеги (а их 31 штука) посчитаны заранее и сохранены в массивах RTable и ImTable, что даёт значительный прирост производительности + к этому сами циклы алгоритма тщательно оптимизированы (часто используемые значения хранятся во временных переменных, используются сдвиговые операции вместо умножения и деления, там где это возможно и т.д).

Заканчивается алгоритм нормировкой, в случае если это ОБПФ, а в случае БПФ нормировка не проводится (здесь мой fft подобен fft, реализованному в MATLAB).

3. Убедиться в корректности работы алгоритмов:

а) проверить выполнение равенства X = ОДПФ (ДПФ(X));

б) сравнить результаты работы реализованного алгоритма, например, с результатами процедуры fft, встроенной в MATLAB.

Для этого выполним скрипт task1.m, его вывод:

Average deviation for labidft(labdft(X)) and X is: 5.8553e-012

Average deviation for labdft(X) and fft(X) is: 2.35408e-010

Скрипт проводит 5 экспериментов, генерируя случайные векторы и проверяя пункты a) и б), как бы видим, разница между начальным вектором и вектором, полученным в результате ОДПФ(ДПФ(X)) примерно равна машинному нулю, то же можно и сказать о разнице labdft(X) и fft(X).

Скрипт task2.m проводит похожие действия для функции labfft и labifft, его вывод:

Average deviation for labifft(labfft(X)) and X is: 6.77889e-011

Average deviation for labfft(X) and fft(X) is: 1.97492e-008

Как мы видим, результат удовлетворительный.

P.S: Для замера времени используются функции tic и toc среды MATLAB, альтернативой можно считать cputime, но в документации MATLAB сказано, что лучше использовать tic и toc, т.к cputime даёт не совсем корректный результат на многокристальных процессорах или на процессорах с включённым гипертредингом.

4. Проанализировать зависимость времени выполнения БПФ и непосредственного вычисления ДПФ от длины N преобразования.

Для этого запустим task3.m, он выведет следующий график:

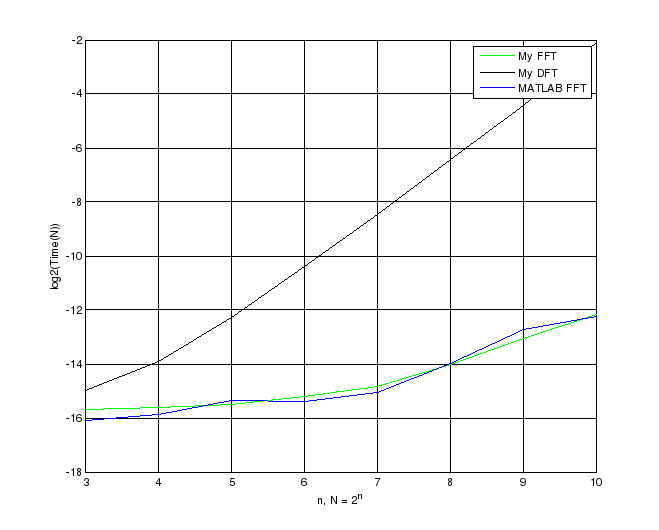
Это логарифмические кривые для 3-х реализаций ПФ:

My FFT – Наше БПФ

My DFT – Наше ДПФ

MATLAB FFT – функция fft в MATLAB’е.

Как мы видим, ДПФ со своей квадратичной сложностью тратит куда больше времени на вычисление, чем БПФ, это можно судить по углу наклона прямой к оси абсцисс, используя Curve Fitting Toolbox найдём уравнения этих прямых:

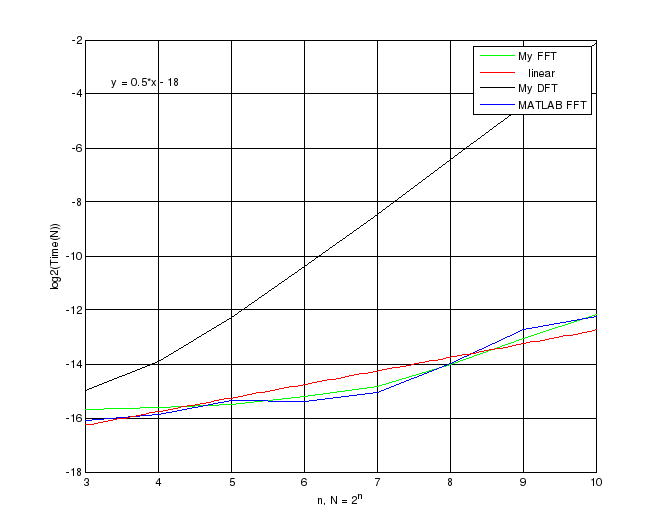
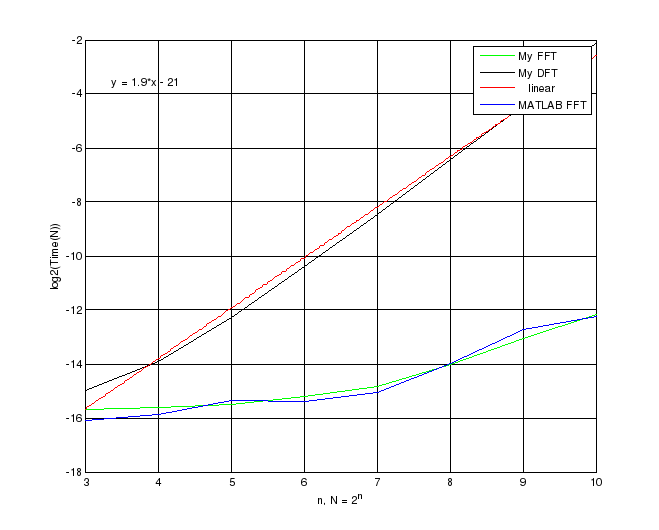
Итак, получили для My FFT – 0.5, для My DFT – 1.9 и для 0.56 для MATLAB FFT. Отсюда сразу можно сделать вывод, что наилучшая функция для вычисления БПФ это My FFT, совсем недалеко от неё идёт MATLAB FFT и далеко позади My DFT. Теперь подсчитаем сложность каждого алгоритма непосредственно.

Итак, имеем графики вида y = a*x + b, здесь x = log(N), а y = log(T(N)), где T(N) – время, которое требуется чтобы выполнить алгоритм для входного вектора, длинны N, т.е получается:

log(T(N)) = a*log(N) + b =>

T(N) = 2^(a*log(N))*2^b

Для алгоритма My DFT получаем:

T(N) = 2^(1.9*log(N))*C, (2^b – постоянная, поэтому её можно просто заменить на C, на асимптотику она всё равно не влияет)

и, следовательно, T(N) = O(N^1.9) ~ O(N^2) – как видим, результат соответствует теоретической оценке.

Для My FFT и MATLAB FFT как известно сложность равна N*log2(N), поэтому с помощью логарифмической прямой ничего конкретного сказать нельзя.

5. Реализовать на С или С++ процедуру прямого вычисления свертки двух последовательностей по формуле (7).

Свёртку считаем по следующему алгоритму:

1. Выявляем наибольшую из двух последовательностей X(длины M) и Y(длины N) (Допустим M<=N)

2. Распишем вычисление свёртки для каждого компонента:

Элемент k

0 от 0 до 0

1 от 0 до 1

.

.

.

M-1 от 0 до M-1

M от 0 до M-1

M+1 от 0 до M-1

.

.

.

N-1 от 0 до M-1

N от 1 до M-1

N+1 от 2 до M-1

.

.

.

N+M-1 от M-1 до M-1

т.е разбиваем вычисление на 3 цикла от 0 до M-1, от M до N-1, и от N до N+M-1. и в каждом цикле организуем соответствующий подцикл. Таким образом мы гарантируем что свёртка будет вычислена максимально быстро, т.к мы не производим лишних вычислений, не умножаем на нуль, не используем условные операторы.

6. Реализовать процедуру нахождения дискретной свертки, основанную на БПФ.

Тут в общем-то без комментариев, алгоритм очевиден.

7. Убедится в корректности работы процедуры из п. 6 задания, сравнив полученные результаты с результатами работы встроенной функций MATLAB conv.

Для этого запускаем task4.m, его работа аналогична работе скриптов task1.m и task2.m, примерный вывод:

Average deviation for labconv(X, Y) and conv(X, Y) is: 1.2544e-011

Average deviation for labfastconv(X, Y) and conv(X, Y) is: 8.94749e-011

И вновь получаем разницу, близкую к машинному нулю.

8. Сравнить производительность алгоритмов вычисления свертки по определению (7) и с помощью БПФ в двух случаях: когда размер одной из последовательностей фиксирован, и когда меняются длины обеих последовательностей.

Первый случай – обе последовательности изменяются в размерах, запускаем task5.m, предварительно выставив переменную OneFixed в false, получаем:

Как видим, свёртка с помощью БПФ работает гораздо лучше обычных свёрток (My conv и MATLAB conv), теперь будем изменять только одну последовательность, зададим OneFixed = true и вновь выполним task5.m, получим:

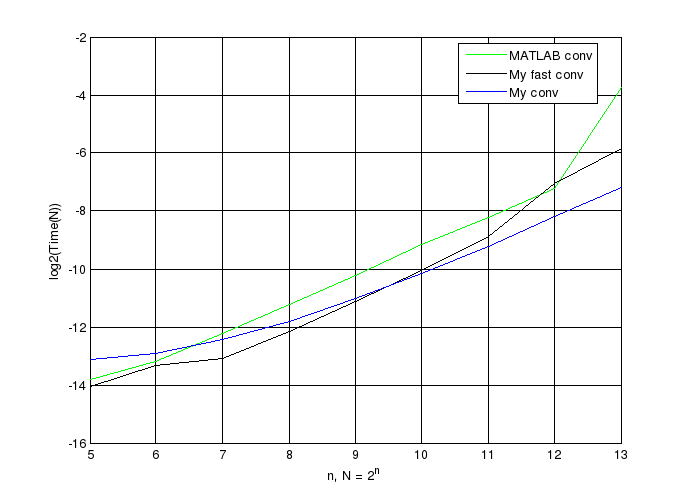
Как видим, здесь БПФ свёртка проигрывает алгоритму My conv, вызвано это следующим: чтобы провести свёртку при помощи My fast conv, нужно сперва привести векторы к одинаковой размерности N = max(2*N1, 2*N2), где N1 и N2 – размеры первого и второго вектора соответственно. Ясно, что когда оба вектора изменяются, то БПФ, проводимые нами работают на, в основном, не нулевых элементах, тоже самое касается и свёртки My conv, поэтому в этом случае свёртка My fast conv быстрее, т.к вычислить два БПФ, быстрее, чем считать по формуле (7).

Во втором случае, когда один из вектором фиксирован происходит вот что: алгоритм My fast conv приводит векторы к одинаковой размерности, тем самым заполняя меньший из них нулями и БПФ проводить значительную часть времени умножая на нули, в то время как My conv быстро считает по формуле (7) (Напомним, что My conv не выполняет лишних действий, благодаря разбивки на 3 цикла, см. выше.)

Дабы доказать что My conv быстрее чем My fast conv во втором случае, воспользуемся Curve Fitting Toolbox:

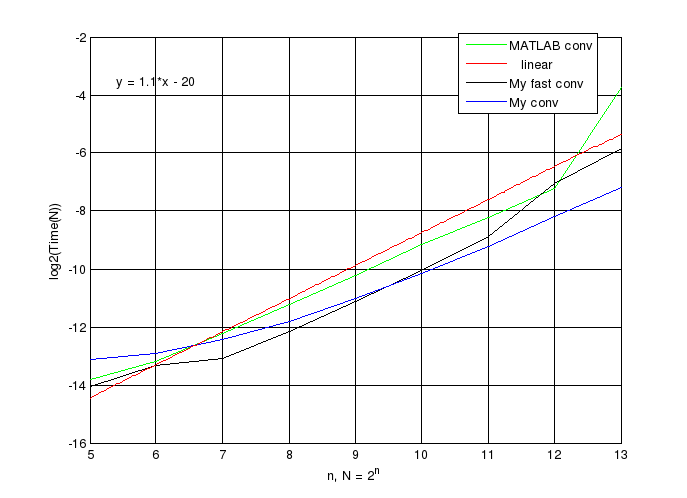
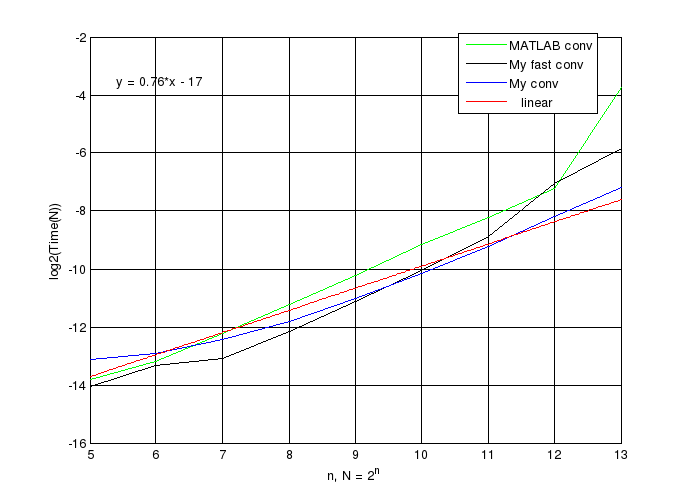
Имеем 0.76 < 1.0 < 1.1.

Работу выполнил: Воробьёв Станислав, МП-40.