
9.Теорема Коши
.pdf
§3. Теорема Коши
Теорема Коши. Если функции f (x) и g(x)
1.определены и непрерывны на отрезке [a, b],
2.дифференцируемы на интервале (a, b),
3.g (x) 0 на интервале (a, b),
то на интервале (a, b) найдѐтся хотя бы одна точка с такая, для которой будет справедливо равенство
f (b) f (a) |
|
f (c) |
, |
(3.1) |
g(b) g(a) |
g (c) |
называемое формулой Коши.
►Из условия теоремы следует, что g(b) g(a) , иначе бы, в силу теоремы Ролля, на интервале (a, b) нашлась бы хотя бы одна точка х0 , в которой бы g (х0) 0 , что противоречит условию g (x) 0 на интервале (a, b).
Рассмотрим вспомогательную функцию
F(x) f (x) f (a) f (b) f (a) g(х) g(а) . g(b) g(a)
Она обладает следующими свойствами:
1)F(x) непрерывна на отрезке [a, b] как алгебраическая сумма
непрерывных функций;
2) F(x) дифференцируема на интервале (a, b) как алгебраическая сумма дифференцируемых функций, при этом
F (x) f (x) |
f (b) f (a) |
g (x) ; |
(3.2) |
|
|||
|
g(b) g(a) |
|
|
3) F(а) F(b) = 0.
Итак, для функции F(x) выполнены условия теоремы Ролля, поэтому на
интервале (a, b) найдѐтся хотя бы одна точка с такая, что F (с) 0. |
При х с |
||||
из (3.2) |
получаем: 0 f (с) |
f (b) f (a) |
g (с) , отсюда следует |
равенство |
|
|
|||||
|
|
|
g(b) g(a) |
|
|
(3.1).◄ |
|
|
|
|
|
Пример 3.1. Проверить справедливость теоремы Коши для |
функций |
||||
f (x) x3 8x и g(x) x2 |
2 2x , заданных на отрезке [2, 4]. |
|
|||
►Для |
f (x) и g(x) |
на отрезке [2,4] выполнены все условия теоремы |
|||
Коши. Поэтому на интервале (2, 4) есть хотя бы одна точка с, для которой
справедлива |
формула |
Коши, |
имеющая в |
данном |
случае |
вид: |
|||||||
|
f (4) |
f (2) |
|
3c2 8 |
или |
40 |
3c2 |
8 |
. Отсюда для с |
получаем уравнение: |
|||
|
g(4) |
|
|||||||||||
|
g(2) |
c 2 |
|
2 |
c 2 |
|
|
|
|
|
|||
3c2 20c 32 0 , |
которое |
имеет |
два корня: |
c 4, c |
8 3. Так |
как |
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
c1 4 (2, 4) , то заключаем, что c 8 3.◄
3.◄
Замечание 3.1. Как и в случае теоремы Ролля, можно привести примеры, показывающие, что условия теоремы Коши существенны для еѐ заключения.
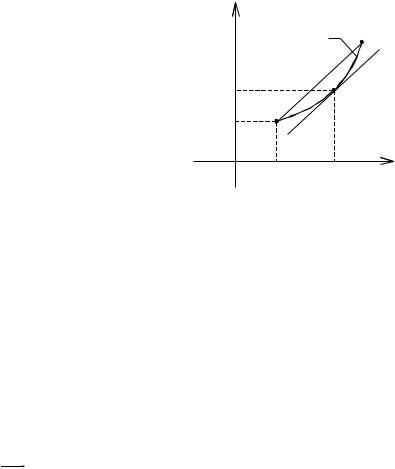
1º. Геометрическая интерпретация теоремы Коши. Пусть дуга Г задана
параметрически: |
x x(t) , |
y y(t) , |
t [α,β] , |
а функции |
x(t) , y(t) |
||||||||||
удовлетворяют |
на |
отрезке |
[α,β] |
условиям |
|
|
y |
|
|
||||||
|
|
|
|
|
y(β) y(α) |
yt (γ) |
|
|
|
|
|
||||
теоремы Коши, поэтому: |
|
|
|
, где |
у (β) |
|
|
|
B |
||||||
x(β) x(α) |
x (γ) |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
T |
|
|
(α,β) (см. (3.1)). Правая часть этого равенства |
у (γ) |
|
|
C |
|
|||||||||
|
yt ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= y (x(γ)) |
– |
угловой |
коэффициент |
у (α) |
|
|
|
|
||||||
|
xt ( ) |
|
|
|
|
||||||||||
|
x |
|
|
|
|
|
|
|
|
|
A |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
касательной, проведѐнной в точке C(х(γ),(y(γ)) к |
|
|
|
|
x |
||||||||||
кривой Г, а левая – угловой коэффициент хорды |
O |
x( ) |
x( ) x( ) |
||||||||||||
|
|
|
|||||||||||||
АВ, А(х(α),(y(α)),B(х(β),(y(β)). |
|
|
|
|
|
Рис. 4.1. К геометрической |
|||||||||
|
|
|
|
|
|
|
интерпретации |
|
|||||||
Итак, |
на кривой Г |
есть точка |
С такая, что |
|
|
|
|||||||||
|
|
теоремы Коши |
|
||||||||||||
проведѐнная в ней касательная Т к Г параллельна |
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||
хорде, соединяющей концы дуги Г (рис. 4.1). |
|
|
|
|
|
||||||||||
|
2º. Физическая интерпретация теоремы Коши. Пусть материальная |
||||||||||||||
точка |
движется |
по |
дуге Г, |
заданной |
параметрически: |
|
x x(t) , |
y y(t) , |
|||||||
[t1, t2 ] . Параметр t трактуется как время, а функции x(t) , |
y(t) удовлетворяют |
||||||||||||||
на этом про |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
межутке условиям теоремы Коши. В силу формулы (3.1) получаем равенство:
y(t2 ) y(t1 ) |
|
y (t*) |
, |
t* (t , t |
2 |
) . Итак, на интервале |
(t , t |
|
) есть момент |
|
|
2 |
|||||||
x(t2 ) x(t1 ) |
x (t*) |
1 |
|
1 |
|
||||
|
|
|
|
|
|
||||
времени t*, в который вектор скорости движения точки v(x (t*), y (t*))
будет коллинеарен вектору AB , где A(x(t1), y(t1)), B(x(t2 ), y(t2 )) – концы дуги Г.
