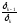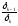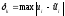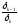Implicit none
include 'link_fnl_static.h'
parameter mxparam=50
!nr - число точек на координатной оси
!nt - число точек на временной оси
real*8 param(mxparam),y(n),yprime(n),t,tend,phi,
& tfinish,ht,tol,yy(n,nt+2),a(1,1),u,htrial,eps,err(n)
integer i,ido,l,m,j,nstep,nfcn,nje
external fcn,fcnj
open(1,file='out_ur.dat')
open(2,file='out_ut.dat')
open(3,file='param.dat')
open(4,file='error.dat')
param=0.0
param(4)=5000000.0 !макс число шагов
param(10)=1.0 !вычисляем абс ошибку
param(12)=2.0 !используем метод Гира дифференцирования назад
param(13)=1.0 !метод хорд с аналит зад якоб
param(14)=1.0 !задаёт ленточный несимм. вид массива dypdy
param(15)=1.0 !число нижних кодиагоналей
param(16)=1.0 !число верхних кодиагоналей
param(19)=0.0 !явная система,матрица А не используется
tol=1.0e-7 !допуск ошибки
rl=2.0d0 !левая граница по радиусу
rr=10.0d0 !правая граница по радиусу
hr=(rr-rl)/(n-1) !шаг по координате
t=0.0d0 !начальный момент времени
ro(1)=rl;y(1)=phi(ro(1))
yy(1,1)=ro(1)
write(*,*)ro(1)
do i=2,n
ro(i)=ro(i-1)+hr !задание основной коорд. сетки
y(i)=phi(ro(i)) !и начальных значений y(i)
write(*,*)ro(i)
yy(i,1)=ro(i) !столбец с координатами точек сетки
if(i.ne.n) then
end if
end do
do i=1,n
yy(i,2)=y(i) !столбец начальных значений
end do
tfinish=10.0d0 !конечный момент времени
ht=tfinish/nt !шаг по времени
ido=1.0 !метка,характериз. стадию вычислений
write(2,88)t,y
do i=1,nt !решение системы из nr дифф. уравнений
tend=t+ht !в момент времени tend
call divpag(ido,n,fcn,fcnj,a,t,tend,tol,param,y)
if(ido==2) then
do l=1,n
yy(l,i+2)=y(l)
end do
write(2,88)t,y !вывод зависимости U(t)в разных точках сетки
else
write(1,*)'ido = ',ido
end if
!вывод погрешности в узлах в разные моменты времени
write(4,*)
do m=1,n
write(4,*) dabs(u(ro(m),t)-y(m))
end do
end do
eps=0.0d0
do i=1,n
if(dabs(y(i)-u(ro(i),t)).gt.eps) then
eps=dabs(y(i)-u(ro(i),t))
end if
end do
do j=1,n !вывод зависимости U(r)в разные мом. времени
write(1,88)(yy(j,i),i=2,nt+2)
end do
write(1,88) t,eps
do i=1,n
write(1,88)ro(i),u(ro(i),t),y(i)
end do
write(1,88)
!вывод параметров для сравнения эффективности программ
nstep=param(34);nfcn=param(35)
nje=param(36);htrial=param(31)
write(3,*)"nstep = ",nstep
write(3,*)"nfcn = ",nfcn
write(3,*)"nje = ",nje
write(3,*)"htrial = ",htrial
ido=3.0
88 format(1x,23(e11.4,1x))
end program task1
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
subroutine fcn(nr,t,y,yprime)
use datamod
real*8 y(nr),yprime(nr),k,q,f,onu,tnu,t
! kapa=0.0d0 !1 u=1
kapa=1.0d0 !3 u=r*e^(-t)
yprime(1)=((rl+0.5d0*hr)*k(rl+0.5d0*hr,t)/hr*(y(2)-
& y(1))+rl*onu(t)-0.5d0*hr*rl*q(rl,t)*y(1)+0.5d0*hr*rl*f(rl,t))/
& (0.5d0*hr*rl)
do i=2,nr-1
yprime(i)=((ro(i)+0.5d0*hr)*k(ro(i)+0.5d0*hr,t)/hr*(y(i+1)-y(i))-
& (ro(i)-0.5d0*hr)*k(ro(i)-0.5d0*hr,t)/hr*(y(i)-y(i-1))-
& hr*ro(i)*q(ro(i),t)*y(i)+hr*ro(i)*f(ro(i),t))/
& (hr*ro(i))
end do
yprime(nr)=(-rr*(kapa*y(nr)-tnu(t))-(rr-0.5d0*hr)*k(rr-0.5d0*hr,t)
&*(y(nr)-y(nr-1))/hr-0.5d0*hr*rr*q(rr,t)*y(nr)+0.5d0*hr*rr*f(rr,t))
& /(0.5d0*hr*rr)
end
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
subroutine fcnj(nr,t,y,dypdy)
use datamod
real*8 t,y(nr),dypdy(3,nr),k,q,f,onu,tnu
!задаём коэфф. матрицы якоби
dypdy(1,1)=0.0d0
dypdy(2,1)=(-(rl+0.5d0*hr)*k(rl+0.5d0*hr,t)/hr-0.5d0*hr*rl*
& q(rl,t))/(0.5d0*hr*rl)
dypdy(3,1)=((ro(2)-0.5d0*hr)*k(ro(2)-0.5d0*hr,t)/hr)/
& (hr*ro(2))
do i=2,nr-1
if(i.eq.2) then
dypdy(1,i)=(ro(i-1)+0.5d0*hr)*k(ro(i-1)+0.5d0*hr,t)/hr/
& (0.5d0*hr*ro(i-1))
else
dypdy(1,i)=(ro(i-1)+0.5d0*hr)*k(ro(i-1)+0.5d0*hr,t)/hr/
& (hr*ro(i-1))
end if
dypdy(2,i)=(-(ro(i)+0.5d0*hr)*k(ro(i)+0.5d0*hr,t)/hr-
& (ro(i)-0.5d0*hr)*k(ro(i)-0.5d0*hr,t)/hr-hr*ro(i)*q(ro(i),t))/
& (hr*ro(i))
if(i.ne.(nr-1))then
dypdy(3,i)=((ro(i+1)-0.5d0*hr)*k(ro(i+1)-0.5d0*hr,t)/hr)/
& (hr*ro(i+1))
end if
end do
dypdy(1,nr)=(ro(nr-1)+0.5d0*hr)*k(ro(nr-1)+0.5d0*hr,t)/hr/
& (hr*ro(nr-1))
dypdy(2,nr)=(-rr*kapa-(rr-0.5d0*hr)*k(rr-0.5d0*hr,t)/hr-
& 0.5d0*hr*rr*q(rr,t))/(0.5d0*hr*rr)
dypdy(3,nr-1)=((ro(nr)-0.5d0*hr)*k(ro(nr)-0.5d0*hr,t)/hr)/
& (0.5d0*hr*rr)
dypdy(3,nr)=0.0d0
end
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
double precision function k(r,t)
real*8 r,t
! k=1.0d0 !1
k=r**2.0d0
end
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
double precision function q(r,t)
implicit real*8 (a-h,k,o-z)
! q=0.0d0 !1
q=r*dexp(0.01d0*t)
end
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
double precision function f(r,t)
real*8 r,t
! f=0.0d0 !1
f=-3.01d0*r*dexp(-0.01d0*t)+r**2
end
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
double precision function onu(t) !ню один
real*8 t
! onu=0.0d0 !1
onu=-4.0d0*dexp(-0.01d0*t)
end
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
double precision function tnu(t) !ню два
real*8 t
! tnu=0.0d0 !1
tnu=110.0d0*dexp(-0.01d0*t)
end
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
double precision function phi(r) !начальное условие
real*8 r
! phi=1.0d0 !1
phi=r
end
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
double precision function U(r,t) !точное решение
real*8 r,t
! u=1.0d0
u=r*dexp(-0.01d0*t)
end
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
8. Зависимость погрешности решения от числа разбиений интервала интегрирования по пространственной переменной в фиксированный момент времени Т (конец интервала интегрирования).
Таблица
результатов работы программы на тестах
(зависимость Чебышевской нормы погрешности
решения от удваивающегося количества
разбиений ).N=20
).N=20
Метод Рунге-Кутта:
|
|
Тест 1 |
|
Тест 2 |
|
|
k |
|
|
|
|
|
1 |
0.0000E+00 |
---- |
0.2217E-01 |
---- |
|
2 |
0.0000E+00 |
---- |
0.5327E-02 |
4,16E+00 |
|
3 |
0.0000E+00 |
---- |
0.1302E-02 |
4,09E+00 |
|
4 |
0.0000E+00 |
---- |
0.3217E-03 |
4,05E+00 |
|
5 |
0.0000E+00 |
---- |
0.7994E-04 |
4,02E+00 |
Табл. 1.
Метод Гира с численным вычислением матрицы Якоби:
|
|
Тест 1 |
|
Тест 2 |
|
|
k |
|
|
|
|
|
1 |
0.0000E+00 |
---- |
0.2217E-01 |
---- |
|
2 |
0.0000E+00 |
---- |
0.5327E-02 |
4,16E+00 |
|
3 |
0.0000E+00 |
---- |
0.1302E-02 |
4,09E+00 |
|
4 |
0.0000E+00 |
---- |
0.3217E-03 |
4,05E+00 |
|
5 |
0.0000E+00 |
---- |
0.8004E-04 |
4,02E+00 |
Табл. 2.
Метод Гира с аналитическим вычислением матрицы Якоби:
|
|
Тест 1 |
|
Тест 2 |
|
|
k |
|
|
|
|
|
1 |
0.0000E+00 |
---- |
0.2217E-01 |
---- |
|
2 |
0.0000E+00 |
---- |
0.5327E-02 |
4,16E+00 |
|
3 |
0.0000E+00 |
---- |
0.1302E-02 |
4,09E+00 |
|
4 |
0.0000E+00 |
---- |
0.3217E-03 |
4,05E+00 |
|
5 |
0.0000E+00 |
---- |
0.8004E-04 |
4,02E+00 |
Табл. 3.
9. Вывод об оценке порядка точности разностной схемы по пространственной переменной по результатам табл. 1-3.
По результатам таблиц 1-3 разностная схема имеет второй порядок точности по пространственной переменной, т.к. с увеличением числа разбиений в два раза чебышевская норма погрешности уменьшается в 4 раза.
10. Оценка эффективности работы подпрограмм IVPRK и IVPAG на тестах.
Тест №1.
Метод Рунге-Кутта.
|
k |
Величина последнего шага |
Число шагов |
Число вычислений правой части |
Число вычислений матрицы Якоби |
|
1 |
0.5 |
23 |
184 |
0 |
|
2 |
0.5 |
23 |
184 |
0 |
|
3 |
0.5 |
23 |
184 |
0 |
|
4 |
0.5 |
23 |
184 |
0 |
|
5 |
0.5 |
23 |
184 |
0 |
Метод Гира с численным вычислением ленточной матрицы Якоби:
|
k |
Величина последнего шага |
Число шагов |
Число вычислений правой части |
Число вычислений матрицы Якоби |
|
1 |
5 |
5 |
46 |
2 |
|
2 |
5 |
5 |
86 |
2 |
|
3 |
5 |
5 |
166 |
2 |
|
4 |
5 |
5 |
326 |
2 |
|
5 |
5 |
5 |
646 |
2 |
Метод Гира с аналитическим вычислением ленточной матрицы Якоби:
|
k |
Величина последнего шага |
Число шагов |
Число вычислений правой части |
Число вычислений матрицы Якоби |
|
1 |
5 |
5 |
6 |
2 |
|
2 |
5 |
5 |
6 |
2 |
|
3 |
5 |
5 |
6 |
2 |
|
4 |
5 |
5 |
6 |
2 |
|
5 |
5 |
5 |
6 |
2 |
Тест №2.
Метод Рунге-Кутта.
|
k |
Величина последнего шага |
Число шагов |
Число вычислений правой части |
Число вычислений матрицы Якоби |
|
1 |
1.653698299275419E-003 |
4871 |
43721 |
0 |
|
2 |
4.256709891485855E-004 |
21532 |
193956 |
0 |
|
3 |
7.387772536304738E-005 |
91012 |
821721 |
0 |
|
4 |
2.003697105834590E-005 |
375523 |
3390318 |
0 |
|
5 |
5.212606627225114E-006 |
1528847 |
13804404 |
0 |
Метод Гира с численным вычислением ленточной матрицы Якоби:
|
k |
Величина последнего шага |
Число шагов |
Число вычислений правой части |
Число вычислений матрицы Якоби |
|
1 |
2.39132091241583 |
119 |
632 |
24 |
|
2 |
2.25971699230220 |
106 |
1059 |
23 |
|
3 |
1.35843331127791 |
87 |
1881 |
22 |
|
4 |
2.74058010078488 |
62 |
2810 |
17 |
|
5 |
3.28309397551500 |
44 |
4222 |
13 |
Метод Гира с аналитическим вычислением ленточной матрицы Якоби:
|
k |
Величина последнего шага |
Число шагов |
Число вычислений правой части |
Число вычислений матрицы Якоби |
|
1 |
2.39132096455194 |
119 |
152 |
24 |
|
2 |
2.25971650989382 |
106 |
139 |
23 |
|
3 |
1.35843352104231 |
87 |
121 |
22 |
|
4 |
2.74058018793197 |
62 |
90 |
17 |
|
5 |
3.28309598153478 |
44 |
62 |
13 |
11. Выводы об эффективности применения подпрограмм IVPRK и IVPAG с использованием явных и неявных методов численного интегрирования.
Самым быстрым методом оказался тот, где использовалась подпрограмма IVPAG с аналитическим вычислением матрицы Якоби. При решении жестких дифференциальных уравнений применение IVPRK оказывается невозможным, а IVPAG справляется с поставленной задачей. В случае данных тестовых задач самым эффективным оказалось применение подпрограммы IVPAG с аналитическим заданием матрицы Якоби.