
- •Глава 1. Основные положения статики.
- •§ 1. Аксиомы и принципы статики твёрдого тела.
- •§ 2. Момент силы относительно произвольного центра, оси.
- •§ 3.Пара сил и её свойства.
- •§ 4.Главный вектор и главный момент системы сил. Правило Пуансо.
- •§ 5. Приведение системы сил к простейшему виду.
- •§ 6. Уравнения равновесия тела.
- •Глава 2. Центр параллельных сил и центр тяжести.
- •§ 1. Центр параллельных сил.
- •§ 2. Центр тяжести, методы определения координат центра тяжести.
- •Глава 3. Равновесие при наличии сил трения.
- •§ 1. Трение скольжения Угол трения, конус трения.
- •§ 2. Задача об опрокидывании тела. Трение качения.
- •Некоторые задачи статики и динамики точки и твёрдого тела.
- •Глава 18 Уравнения статики деформируемого твёрдого тела.
- •§ 1. Дифференциальные уравнения равновесия нерастяжимой нити.
- •§ 2. Статика деформируемых прямых стержней.
- •1.Статика.
§ 5. Приведение системы сил к простейшему виду.
Как
выше было доказано, произвольная система
сил, как угодно расположенных в
пространстве, может быть приведена к
одной силе, равной главному вектору
 системы и приложенной в произвольном
центре приведенияО,
и одной паре с моментом
системы и приложенной в произвольном
центре приведенияО,
и одной паре с моментом
 ,
равным главному моменту системы
относительно того же центра. По
,
равным главному моменту системы
относительно того же центра. По
|
|
|
Рис 8 |
 и момента
и момента ,
приложенных в точкеО.
При изменении положения центра приведения
О главный
вектор
,
приложенных в точкеО.
При изменении положения центра приведения
О главный
вектор
 будет сохранять величину и направление,
а главный момент
будет сохранять величину и направление,
а главный момент будет изменяться. Докажем, что если
главный вектор и главный момент отличны
от нуля и взаимно
перпендикулярны, то система сил приводится
к одной силе, которую в этом случае будем
называть равнодействующей
будет изменяться. Докажем, что если
главный вектор и главный момент отличны
от нуля и взаимно
перпендикулярны, то система сил приводится
к одной силе, которую в этом случае будем
называть равнодействующей
 (рис.8). Главный момент
(рис.8). Главный момент можно представить парой сил (
можно представить парой сил ( ,
, )
с плечом
)
с плечом
 ,
тогда силы
,
тогда силы и главный век тор
и главный век тор образуют
систему двух сил эквивалентную
нулю, которую можно отбросить. Останется
одна сила
образуют
систему двух сил эквивалентную
нулю, которую можно отбросить. Останется
одна сила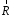 ,
действующая вдоль прямой, параллельной
главному вектору и проходящей на
расстоянииh=
,
действующая вдоль прямой, параллельной
главному вектору и проходящей на
расстоянииh= от плоскости, образуемой векторами
от плоскости, образуемой векторами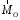 и
и .
Рассмотренный случай показывает, что
если с самого начала выбрать центр
приведения на прямой L,
то систему сил сразу бы привели к
равнодействующей, главный момент был
бы равен нулю. Теперь докажем, что если
главный вектор отличен от нуля и не
перпендикулярен к главному моменту, то
за центр приведения может быть выбрана
такая точка О*,
что главный момент относительно этой
точки и главный вектор расположатся на
одной прямой. Для доказательства разложим
момент
.
Рассмотренный случай показывает, что
если с самого начала выбрать центр
приведения на прямой L,
то систему сил сразу бы привели к
равнодействующей, главный момент был
бы равен нулю. Теперь докажем, что если
главный вектор отличен от нуля и не
перпендикулярен к главному моменту, то
за центр приведения может быть выбрана
такая точка О*,
что главный момент относительно этой
точки и главный вектор расположатся на
одной прямой. Для доказательства разложим
момент
 на
две составляющие- одну
на
две составляющие- одну ,
направленную вдоль главного вектора,
и другую
,
направленную вдоль главного вектора,
и другую - перпендикулярную к главному вектору.
Тем самым пара сил
- перпендикулярную к главному вектору.
Тем самым пара сил раскладывается на две пары с моментами:
раскладывается на две пары с моментами: и
и ,
причем плоскость первой пары
перпендикулярна к
,
причем плоскость первой пары
перпендикулярна к ,
тогда плоскость второй пары,
перпендикулярная к вектору
,
тогда плоскость второй пары,
перпендикулярная к вектору (рис 9) содержит вектор
(рис 9) содержит вектор .
Совокупность пары с моментом
.
Совокупность пары с моментом и
силы
и
силы образует
систему сил, которая может быть сведена
к одной силе (рис.8) , проходящей через
точку О* . Таким образом (рис 9), совокупность
главного вектора
образует
систему сил, которая может быть сведена
к одной силе (рис.8) , проходящей через
точку О* . Таким образом (рис 9), совокупность
главного вектора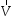 и главного момента
и главного момента в точкеО
сведена к силе
в точкеО
сведена к силе
 ,
проходящей через точкуО*,
и паре с моментом параллельным этой
прямой
,
проходящей через точкуО*,
и паре с моментом параллельным этой
прямой
 ,
что и требовалось доказать. Совокупность
силы и пары, плоскость которой
перпендикулярна к линии действия силы,
называется динамой (рис.10). Пару сил
можно представить двумя равными по
величине силами (
,
что и требовалось доказать. Совокупность
силы и пары, плоскость которой
перпендикулярна к линии действия силы,
называется динамой (рис.10). Пару сил
можно представить двумя равными по
величине силами ( ,
, ),
расположенными как показано на рис 10.
Но, сложив две силы
),
расположенными как показано на рис 10.
Но, сложив две силы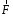 и
и ,
получим их сумму
,
получим их сумму и оставшуюся силу
и оставшуюся силу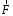 ,
откуда следует (рис.10), что совокупность
главного вектора
,
откуда следует (рис.10), что совокупность
главного вектора и главного момента
и главного момента в точкеО,
может быть сведена к двум непересекающимся
силам
в точкеО,
может быть сведена к двум непересекающимся
силам
 и
и .
.
Рассмотрим
некоторые случаи приведения системы
сил.
1. Плоская система сил. Пусть для определённости все силы находятся в плоскости OXY. Тогда в самом общем случае
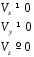

Главный вектор не равен нулю, главный момент не равен нулю, их скалярное произведение равно нулю, действительно
 ,
,
следовательно, главный вектор перпендикулярен главному моменту: плоская система сил приводится к равнодействующей.
2. Система параллельных сил. Пусть для определённости все силы параллельны оси OZ. Тогда в самом общем случае


Здесь также главный вектор не равен нулю, главный момент не равен нулю, а их скалярное произведение равно нулю, действительно
 ,
,
следовательно,
главный вектор перпендикулярен главному
моменту: система параллельных сил
приводится к равнодействующей. В частном
случае, если
 равна нулю, то и главный вектор сил равен
нулю, и система сил приводится к паре
сил, вектор момента которой находится
в плоскостиOXY.
Систематизируем теперь рассмотренные
случаи. Напомним: произвольная
пространственная система сил, приложенная
к твердому телу, статически эквивалентна
силе, равной главному вектору, приложенной
в произвольной точке тела (центре
приведения), и паре сил с моментом, равным
главному моменту системы сил относительно
указанного центра приведения.
равна нулю, то и главный вектор сил равен
нулю, и система сил приводится к паре
сил, вектор момента которой находится
в плоскостиOXY.
Систематизируем теперь рассмотренные
случаи. Напомним: произвольная
пространственная система сил, приложенная
к твердому телу, статически эквивалентна
силе, равной главному вектору, приложенной
в произвольной точке тела (центре
приведения), и паре сил с моментом, равным
главному моменту системы сил относительно
указанного центра приведения.
1)
Пусть
 =0,
=0, ≠0.
Это случай, когда система сил приводится
к одной силе, которую будем называть
равнодействующей системы сил. Примером
такой системы сил можно считать сходящуюся
систему сил, для которой линии действия
всех сил пересекаются в одной точке.
≠0.
Это случай, когда система сил приводится
к одной силе, которую будем называть
равнодействующей системы сил. Примером
такой системы сил можно считать сходящуюся
систему сил, для которой линии действия
всех сил пересекаются в одной точке.
2)
 ≠0,
≠0, =0
. Система сил эквивалентна паре сил.
=0
. Система сил эквивалентна паре сил.
3)
 ≠0,
≠0, ≠0,
но
≠0,
но .
Главный вектор не равен нулю, главный
момент не равен нулю, их скалярное
произведение равно нулю, т.е. главный
вектор и главный момент ортогональны.
Любая система векторов, у которой главный
вектор и главный момент не равны нулю
и они перпендикулярны, эквивалентна
равнодействующей, линия действия
которой проходит через точкуО*
(рис 8). Примером такой системы сил можно
считать плоскую систему сил или
систему параллельных сил.
.
Главный вектор не равен нулю, главный
момент не равен нулю, их скалярное
произведение равно нулю, т.е. главный
вектор и главный момент ортогональны.
Любая система векторов, у которой главный
вектор и главный момент не равны нулю
и они перпендикулярны, эквивалентна
равнодействующей, линия действия
которой проходит через точкуО*
(рис 8). Примером такой системы сил можно
считать плоскую систему сил или
систему параллельных сил.
4)
 ≠0,
≠0, ≠0,
и главный вектор и главный момент
неортогональны. В этом случае система
сил приводится к динаме или к двум
непересекающимся силам.
≠0,
и главный вектор и главный момент
неортогональны. В этом случае система
сил приводится к динаме или к двум
непересекающимся силам.

