
- •1 Информация и информационные процессы в природе, обществе, технике. Информационная деятельность человека. Привести примеры.
- •2Информатика. Определение. Основные направления информатики.
- •3Основные этапы развития вычислительной техники. Информатизация общества.
- •4 Качественные и количественные характеристики информации. Свойства информации. Единицы измерения количества информации.
- •5Кодирование информации, его способы. Привести примеры.
- •6 Арифметические основы компьютера. Системы счисления. Определение системы счисления. Позиционные и непозиционные системы счисления.
- •7 Двоичная система счисления. Запись чисел в двоичной системе счисления.
- •8 Восьмеричная система счисления. Запись чисел в восьмеричной системе счисления. Привести примеры.
- •Алгоритм перевода из 8-ой в 2-ую
- •9 Шестнадцатеричная система счисления. Запись чисел в шестнадцатеричной системе счисления. Привести примеры.
- •Примеры:
- •Алгоритм перевода чисел из 16-ой в 2-ую
- •10 Перевод чисел из десятичной системы счисления в любую другую позиционную систему счисления. Привести примеры.
- •11 Перевод чисел из двоичной, восьмеричной и шестнадцатеричной систем счисления в десятичную систему счисления. Привести примеры.
- •12 Перевод чисел из одной позиционной системы счисления в другую. Привести примеры.
- •13 Арифметические операции в позиционных системах счисления. (в двоичной, восьмеричной и шестнадцатеричной). Привести примеры.
- •14 Что такое компьютер. Классификация компьютеров по поколениям.
- •15 Краткая историческая справка.
- •16 Функциональная схема компьютера. Основные устройства компьютера, их назначения и взаимосвязь.
- •17 Основные характеристики компьютера. (Объём оперативной и внешней памяти, разрядность и т.Д.).
- •18 Внешняя память компьютера. Различные виды носителей информации.
- •19 Программное управление работой компьютера. Программное обеспечение компьютера.
- •20 Что такое мультимедиа.
- •21 Что такое операционная система. Основные функции операционной системы. Привести примеры операционных систем.
- •22 Файловая система. Основные операции с файлами в операционной системе.
- •23 Что такое транслятор, компилятор, интерпретатор.
- •24 Алгебра логики. Что такое логическая формула.
- •27 Логическое сложение и умножение.
- •28 Основные законы алгебры логики.
- •29 Таблица истинности для логической формулы.
- •30 Этапы решения задач на эвм
- •31 М оделирование, как метод научного познания. Модели физические и математические. Привести примеры.
- •32 Алгоритм. Свойства алгоритма. Виды алгоритмов.
- •33 Алгоритмическая структура «ветвление». Привести примеры.
- •34 Алгоритмическая структура «цикл». Привести примеры.
- •35 Одномерные массивы и алгоритмы их обработки. Привести примеры.
- •36 Двумерные массивы и алгоритм их обработки. Привести примеры.
- •37 Язык и информация. Естественные и формальные языки
- •38 Языки программирования
- •39 Общая характеристика языка Turbo-Pascal.
- •40 Алфавит, синтаксис, семантика языка Turbo-Pascal.
- •41 Классификация типов данных языка.
- •42 Операторы. Классификация операторов.
- •43 Структура программы на языке Turbo-Pascal.
- •44 Простые и структурированные операторы языка.
- •45 Логические операторы языка Turbo-Pascal.
- •46 Ввод и вывод данных в языке Turbo-Pascal. Привести примеры.
27 Логическое сложение и умножение.
1) Логическое умножение или конъюнкция:
Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
Таблица истинности для конъюнкции
A B F
1 1 1
1 0 0
0 1 0
0 0 0
2 Логическое сложение или дизъюнкция:
Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
A B F
1 1 1
1 0 1
0 1 1
0 0 0
28 Основные законы алгебры логики.
Вот как трактует логику толковый словарь: "Логика - наука, изучающая способы обоснования суждений, доказательства, мышления и логического вывода. В математической логике используются для этого методы алгебры или теории алгоритмов". "Алгебра логики (булева алгебра) - раздел математики, изучающий методы оперирования логическими (булевыми) переменными, принимающими только два значения - истина и ложь. Предложен английским математиком Джорджем Булем". Добавим только, что помимо манипуляций константами "да" и "нет" логические переменные могут являться результатом применения к числам операторов отношения (меньше, больше, равно и т.п.).
В компьютерах булевы переменные представляются (кодируются) битами (разрядами двоичной системы счисления), где 1 обычно означает истину, а 0 - ложь. Вот ещё одно достоинство двоичной системы счисления!
В алгебре логики имеются законы, которые записываются в виде соотношений. Логические законы позволяют производить равносильные (эквивалентные) преобразования логических выражений. Преобразования называются равносильными, если истинные значения исходной и полученной после преобразования логической функции совпадают при любых значениях входящих в них логических переменных.

Для простоты записи приведем основные законы алгебры логики для двух логических переменных А и В. Эти законы распространяются и на другие логические переменные.
1. Закон противоречия:
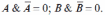
2. Закон исключенного третьего:
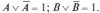
3. Закон двойного отрицания:
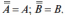
4. Законы де Моргана:
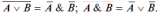
5. Законы повторения: A & A = A; A v A = A; В & В = В; В v В = В.
6. Законы поглощения: A ∨ (A & B) = A; A & (A ∨ B) = A.
7. Законы исключения констант: A ∨ 1 = 1; A ∨ 0 = A; A & 1 = A; A & 0 = 0; B ∨ 1 = 1; B ∨ 0 = B; B & 1 = B; B & 0 = 0.
8. Законы склеивания:
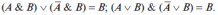
9. Закон контрапозиции: (A ⇔ B) = (B ⇔ A).
Для логических переменных справедливы и общематематические законы. Для простоты записи приведем общематематические законы для трех логических переменных A, В и С:
1. Коммутативный закон: A & B = B & A; A ∨ B = B ∨ A.
2. Ассоциативный закон: A & (B & C) = (A & B) & C; A ∨ (B ∨ C) = (A ∨ B) ∨ C.
3. Дистрибутивный закон: A & (B ∨ C) = (A & B) ∨ (A & C).
Основы логики, Джордж Буль, булева алгебра
Как уже отмечалось, с помощью законов алгебры логики можно производить равносильные преобразования логических выражений с целью их упрощения. В алгебре логики на основе принятого соглашения установлены следующие правила (приоритеты) для выполнения логических операций: первыми выполняются операции в скобках, затем в следующем порядке: инверсия (отрицание), конъюнкция ( & ), дизъюнкция (v), импликация (⇒), эквиваленция (⇔)
Выполним преобразование, например, логической функции
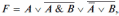
применив соответствующие законы алгебры логики.

