
- •Уравнение линии на плоскости.
- •Параметрическое уравнение линии.
- •2. Полярная система координат (пск).
- •Связь между декартовыми и полярными координатами точки.
- •Классификация плоских линий.
- •Уравнение поверхности в пространстве.
- •Классификация поверхностей.
- •4. Прямая на плоскости.
- •Неполные уравнения прямой. (Частные случаи).
- •Каноническое уравнение прямой.
- •Параметрическое уравнение прямой.
- •Уравнение прямой, проходящей через 2 заданные точки.
- •Уравнение прямой в отрезках.
- •Уравнение прямой с угловым коэффициентом.
- •Взаимное расположение прямых на плоскости.
- •Нормированное (нормальное) уравнение прямой.
- •Уравнение пучка прямых.
- •Расстояние от точки до прямой. Кривые II –го порядка.
- •Аналитическая геометрия в пространстве (r3)
4. Прямая на плоскости.
Теорема. Любая прямая на плоскости представляет собой алгебраическую кривую 1-го порядка и любая алгебраическая кривая 1-го порядка на плоскости есть прямая.
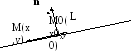 Доказательство.
Рассмотрим произвольную прямую L
на плоскости. Пусть точка М0(х0;у0)
лежит на L,
а ненулевой вектор n={А;В}
перпендикулярен этой прямой. Пусть
точка М(х,у) –
произвольная точка. Точка М(х,у)
Доказательство.
Рассмотрим произвольную прямую L
на плоскости. Пусть точка М0(х0;у0)
лежит на L,
а ненулевой вектор n={А;В}
перпендикулярен этой прямой. Пусть
точка М(х,у) –
произвольная точка. Точка М(х,у) Lкогда
вектор
Lкогда
вектор
![]() =(х-х0)i+(y-y0)j
=(х-х0)i+(y-y0)j вектору n=Ai+Bj
вектору n=Ai+Bj
Т.е.
 n=0
(х-х0)А+(y-y0)В=0
или
n=0
(х-х0)А+(y-y0)В=0
или
Преобразуем уравнение (1): Ах+Ву-Ах0-Ву0=0
Обозначим -Ах0-Ву0=С. Получим следующее уравнение:
Ах+Ву+С=0 (1) – общее уравнение прямой. (т.к. n0, то либо А0, либо В0, т.е. А2+В2≠0). Т.о. первой утверждение доказано.
Для
доказательства второго утверждения,
рассмотрим произвольное уравнение 1-го
порядка с двумя неизвестными Ах+Ву+С=0
(А2+В2≠0).
Это уравнение имеет хотя бы одно решение.
Например, если А0,
то решением уравнения является х=- ,
у=0. Это означает, что существует хотя
бы одна точка М0(х0;у0),
координаты которой удовлетворяют
уравнению (1), т.е. Ах0+Ву0+С=0
(2).
,
у=0. Это означает, что существует хотя
бы одна точка М0(х0;у0),
координаты которой удовлетворяют
уравнению (1), т.е. Ах0+Ву0+С=0
(2).
Вычитая из уравнения (1) равенство (2), получим А(х-х0)+В(y-y0)=0 (3).
Покажем, что уравнение (3), эквивалентное уравнению (1), определяет относительно системы Оху прямую L, проходящую через точку М0(х0;у0) и перпендикулярную вектору n={А;В} (т.к. А2+В2≠0, то вектор n – ненулевой).
Если
точка М(х,у) лежит на прямой L,
то ее координаты удовлетворяют уравнению
(3), т.к. в этом случае векторы n={А;В}
и
![]() ={х-х0;y-y0}
ортогональны и их скалярное произведение
={х-х0;y-y0}
ортогональны и их скалярное произведение
 n=0
(х-х0)А+(y-y0)В=0.
n=0
(х-х0)А+(y-y0)В=0.
Если
же М(х,у) не лежит на прямой L,
то ее координаты не удовлетворяют
уравнению (3), т.к. в этом случае векторы
n={А;В}
и
![]() ={х-х0;y-y0}
не ортогональны и их скалярное произведение
(х-х0)А+(y-y0)В
не равно нулю. Ч.т.д.
={х-х0;y-y0}
не ортогональны и их скалярное произведение
(х-х0)А+(y-y0)В
не равно нулю. Ч.т.д.
Уравнение Ах+Ву+С=0 (1) – общее уравнение прямой
n={А;В} – нормальный вектор прямой L.
Замечание. Если два общих уравнения Ах+Ву+С=0 и А1х+В1у+С1=0 определяют одну и ту же прямую, то найдется такое число t, что A1=At, B1=Bt, C1=Ct (4)
Действительно, т.к. прямые Ах+Ву+С=0 и А1х+В1у+С1=0 совпадают, то векторы n={А;В} и n1={А1;В1} коллинеарны, следовательно, по условию коллинеарности векторов, найдется такое число t, что n1=ntиз линейного свойства координат вектора следуют первые два равенства (4). Т.к. прямые совпадают, то они имеют общую точку М0(х0;у0). Т.е. Ах0+Ву0+С=0 и А1х0+В1у0+С1=0. Вычитая из 2-го равенства 1-е, умноженное на t, получаем (At-А1)х0+(Bt-В1)у0+(Ct-С1)=0 Ct-С1=0 Ct=С1.
Т.о. общее уравнение прямой, как и нормальный вектор прямой, определяется с точностью до ненулевого числового множителя.
Неполные уравнения прямой. (Частные случаи).
Общее уравнение прямой называется полным, если все его коэффициенты не равны 0. в противном случае уравнение называется неполным.
1)
С=0
 Ах+Ву=0 прямая,
проходящая через начало координат.
Ах+Ву=0 прямая,
проходящая через начало координат.
 2)
А=0
2)
А=0
 Ву+С=0 или у=
Ву+С=0 или у= прямая, параллельная оси абсцисс Ох.
(Нормальный вектор n={0;В}
ортогонален оси Ох).
прямая, параллельная оси абсцисс Ох.
(Нормальный вектор n={0;В}
ортогонален оси Ох).
 3)
В=0
3)
В=0
 Ах+С=0 или х=
Ах+С=0 или х= прямая, параллельная оси ординат Оу.
(Нормальный вектор n={А;0}
ортогонален оси Оу).
прямая, параллельная оси ординат Оу.
(Нормальный вектор n={А;0}
ортогонален оси Оу).
4) В=С=0 уравнение Ах=0 определяет ось Оу (т.к. параллельна оси Оу и проходит через начало координат).
5) А=С=0 уравнение Ву=0 определяет ось Ох (т.к. параллельна оси Ох и проходит через начало координат).
