Дифференцирование функций, заданных параметрически.
При
параметрическом задании функции
независимая и зависимая переменные
выражаются через параметр.
 (1)
(1)
Если рассматривать
х и у как прямоугольные координаты точки
на плоскости, то уравнения (1) каждому
значению параметра t
ставят в соответствие некоторую точку,
которая с изменением t
описывает кривую на плоскости. Уравнения
(1) называют параметрическими уравнениями
этой кривой.
Предполагая, что
обе эти функции имеют производные и что
для первой из них существует обратная
функция t=φ-1(x),
имеющая производную, получим, что у
является функцией от х: y=ψ(φ-1(t))=f(x).
для которой также
существует производная, которую можно
вычислить по правилу для вычисления
дифференциала сложной функции:
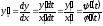 (2)
(2)
В случае
параметрического задания кривой, формула
(2) позволяет по уравнениям (1) установить
угловой коэффициент касательной, не
переходя к заданию кривой в явном виде:
 .
.
Пример.
Найти производную
функции
 циклоида
циклоида
 =
=
Чтобы найти
 замечаем, что функция
замечаем, что функция параметрически задается уравнениями
параметрически задается уравнениями ,
где ψ1(t)=
,
где ψ1(t)=
 или ψ1(t)=
или ψ1(t)=
 .
.
Тогда
 =
= =
=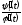 =
=
В рассмотренном
примере
 =
=
Аналогично, считая,
что функция
 задана параметрически уравнениями
задана параметрически уравнениями
 ,
где ψ2(t)=
,
где ψ2(t)=

Находим
 =
= =
= и т.д.
и т.д.



 (1)
(1)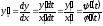 (2)
(2) .
. циклоида
циклоида =
=
 замечаем, что функция
замечаем, что функция параметрически задается уравнениями
параметрически задается уравнениями ,
где ψ1(t)=
,
где ψ1(t)=
 или ψ1(t)=
или ψ1(t)=
 .
. =
= =
=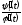 =
=
 =
=
 задана параметрически уравнениями
задана параметрически уравнениями ,
где ψ2(t)=
,
где ψ2(t)=

 =
= =
= и т.д.
и т.д.