Дифференциальное исчисление. Производная.
Пусть функция у=f(x) определена в некоторой окрестности V(x0) точки х0.
Дадим значению аргумента х0 приращение ∆х=х-х0 такое, что х≠0 и точка х=х0+хV(x0). Тогда функция получит приращение
у=f(x)-f(x0) или у=f(х0+х)-f(x0) – приращение функции.
Рассмотрим предел отношения приращения функции к приращению аргумента при приближении точки х к х0.
Определение. Если существует предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю, то этот предел называется производной функции в точке х0:
(1)
Или 
(2)
Обозначения:
,
,
,
.
Если предел
конечен, то производная называется
конечной, если он бесконечен, то
производная называется бесконечной.
Процесс вычисления производных функций
называетсядифференцированием;
точка х0,
в которой вычисляется
производная, называется точкой
дифференцирования.
Пример. Найдем по определению производную функций:
1) f(x)=С, f(x)=0.
2) f(x)=cos x
=
=
=
=
=-2sin
x0·
=-sin
x0. Т.о.
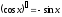
3) f(x)=sin x
=
=
=
=
=-2
cos
x0=
cos x0.
4) f(x)=xn (nN)
1. Случай n=1.
f(x)=x
=
2. n=2,3,…
Воспользуемся формулой бинома Ньютона:
=
=
→
прих→0,
(xn)=nxn-1.
5) f(x)=ax
=
=
=
Введем замену,
t=a∆x-1→0
при ∆х→0. Тогда а∆х=t+1;
∆x=loga(t+1)=
Получаем:
=
=
=
=
=
=
=
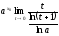Т.о.
в частности,
6) f(x)=logax
=
=
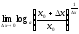
В силу непрерывности функции f(x)=logax f(x)=logax имеем
Т.о.
Примеры
функций, не имеющих производную.
1) f(x)=sign
x=
В точке х0=0 нет производной
f(0+x)-f(0)=
=
- нет предела прих→0
2) f(x)=х- в точке х0=0 нет производной (в положительной полуплоскости f(x)=х, в отрицательной - f(x)=-х). (График)
f(0+x)-f(0)=
,
,
нет предела при х→0
Геометрический смысл производной.
Задача о касательной к кривой. Пусть на плоскости задана непрерывная кривая L, описываемая уравнением у=f(x). Требуется найти уравнение касательной к ней в точке М0(х0,у0).
Определение. Касательной к кривой L в точке х0 называется предельное положение секущей М0М, проходящей через точку М0 и некоторую другую точку М, лежащую на кривой L, когда точка М вдоль кривой произвольным образом стремиться к совпадению с точкой М0, т.е. при Δх→0.
Дадим аргументу х0 приращение Δх такое, что х≠0 и перейдем на кривой от точки М0(х0,f(x0)) к точке М(х0+Δx, f(x0+Δx)) или М(х0+Δx,у0+Δу) (у=f(x0+Δx)-f(x0), у0=f(x0)) и проведем секущую М0М. Она имеет уравнение
у-у0=k(х)(x-x0) (1)
Угловой коэффициент секущей М0М можно найти из ∆ М0МN:
=tgφ=
(2)
Равенство (2) справедливо при любом расположении кривой L и при любом Расположении точки М относительно точки М0 (справа или слева). При х→0 расстояние М0М→0.
Действительно, в
силу непрерывности функции f(x)
в точке х0
будет
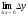=0.
ТогдаМ0М=
→0
прих→0
и точка М по кривой будет стремиться к
совпадению с точкой М0,
секущая М0М
будет стремиться принять свое предельное
положение М0Т,
tg→tg,
x→0
Тогда угловой коэффициент касательной
k=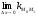
=
=
Т.о., если у функции f(x) в точке x0, то уравнение касательной к графику функции y=f(x) в точке М0(х0,у0) будет иметь вид:
у-у0=
(x-x0) или
у-f(x0)=
(x-x0)
Т.о. получили
геометрический
смысл производной:
производная
- угловой коэффициент (тангенс угла
наклона) касательной, проведенной к
кривой у=f(x) в точке х0,
т.е. k=
.
Если у функции у=f(x) в точке х0 существует бесконечная производная, т.е.
=,
то в силу равенства
=tgφ=
,
=.
Запишем уравнение
секущей М0М
у-у0=k(х)(x-x0)
в виде:
Переходя в этом соотношении к пределу при х→0, получим: х-х0=0х=х0 (4)
(4) -уравнение
касательной к графику функции у=f(x) в
точке М0
в случае, когда
=.
Прямая х=х0
– вертикальная
касательная
к
графику функции
у=f(x) в точке М0.
Механический смысл производной.
Задача о скорости движения. Пусть некоторая материальная точка движется по прямой по закону S=S(t), где S – некоторый путь, t – время. Требуется найти скорость точки в данный момент t (мгновенную скорость).
Перейдем от момента t к моменту t+Δt. За промежуток времени от t до t+Δt точка М пройдет путь ΔS=f(t+Δt)-f(t).
Тогда
за промежуток времени от t до t+Δt (т.е. за
время Δt) средняя скорость будет Vср.=
.
Если движение точки М не является равномерным, то Vср. будет изменяться при изменении Δt. При этом, чем меньше промежуток времени Δt, тем лучше Vср. характеризует движение точки в момент t. Поэтому скоростью точки в момент t является предел Vср. за промежуток от t до t+Δt , когда Δt→0, т.е.
V(t)=
Т.о. получили
механический
смысл производной:
производная пути по времени
- скорость точки в момент t: V(t)=
.
Если скорость движения v не постоянна и сама изменяется с течением времени t: v=f(t), то рассматривают ускорение – «скорость изменения скорости».
А именно, если приращению t отвечает приращение скорости v, то отношение
аср.=
выразит среднее ускорение за промежуток времени t, а предел его даст ускорение движения в данный момент времени:
а=
=
=
Т.о., ускорение является производной скорости от времени.