Правила дифференцирования.

Пусть функции U=U(x), V=V(x) дифференцируемы в точке х₀, тогда функции U±V, UV, CU, U/V также дифференцируемы в этой точке и справедливы равенства:

1. =0, где С=const

2. 

3. 

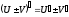
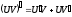
4. (V≠0)

Доказательство. 2) Дадим х приращение х. Тогда функции u(x) и v(x) получат соответственно приращения u и v, их новыми значениями будут u(x)+u и v(x)+v (т.к.

u=u(x+x)-u(x), v=v(x+x)-v(x))

Пусть y=uv, тогда

y=[(u(x)+u)(v(x)+v)]-[u(x)v(x)]=u(x)+uv(x)v-u(x)v(x)=uv

3. Приращение функции у=UV:

у+∆у=(u(x)+∆u)(v(x)+∆v)-uv=u(x)v(x)+∆uv(x)+u(x)∆v+∆u∆v-u(x)v(x)=

=∆uv(x)+u(x)∆v+∆u∆v

Рассмотрим отношение приращений функции и аргумента:

=

Т.к. функция u=u(x) дифференцируема в точке х, то она непрерывна, следовательно , т.е.=0.

(или =0)

Т.о. =ч.т.д.

Доказательство 4. Представим функцию у=в виде у=u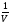 и сведем к предыдущему случаю.

==-=

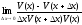Тогда ч.т.д.

Следствие 1. Постоянный множитель можно выносить за знак производной.

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведения производной каждого из сомножителей на все остальные, например:

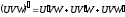
Таблица производных.

1. С=0 (С=const)

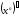2. =nx^n-1

3. 

4. 

5. 6.

7. 8.

9. 10.

11. 12.

Пример. Вывод производной функции у=tg x и у=ctg x, используя правило 4.

Формула для приращения функции.

Пусть функция у= f(y) определена в промежутке Х и в точке х₀Х имеет конечную производную . Придадим х₀ произвольное приращение х≠0 и х₀+хХ. Положим (*)

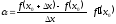Ясно, что  зависит от х (=(х)) и

Из соотношения (*) находим f(x₀+x)-f(x₀)=[+(x)]x

или у=[+(x)]x (**) – формула для приращения функции.

Мы установили формулу (**) для х≠0, т.к. при х=0 соотношение (*) теряет смысл. Если доопределить функцию (х) в точке х=0, то формулу (**) будет верна и для х=0. Будем полагать (0)=0. Тогда формула (**) будет верной как для х≠0, так и для х=0 и соотношение будет верно независимо от того, по какому законух→0 (хотя бы х и принимало значение нуль).

Производная сложной функции.

Пусть даны функции f и φ: . Т.е. функцияy=f(u) определена в промежутке U, а функция u=(х) определена в промежутке Х и если хХ, то (х)U. Тогда для хХ имеет смысл выражение F(x)=f((x)) – сложная функция.

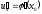Теорема. Пусть 1) функция u=(x) имеет в некоторой точке х₀ производную , 2) функция у=f(u) имеет в соответствующей точке u₀=(x₀) производную . Тогда сложная функция y=f((x)) так же имеет производную в точке х₀ и она равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной, т.е.

Доказательство. Придадим х₀ произвольное приращение х≠0 и х₀+хХ. Тогда функция u=(х) получит приращение u=(х₀+х)-(х₀).

Т.к. y=f(u), то приращению u соответствует приращение y=f(u₀+u)-f(u₀).

По формуле приращения функции (**)y=[+(u)]u,

где (u)→0, при u→0. Тогда =[+(u)]

Пусть х0. Тогда, т.к. функция u=(х) дифференцируема в точке х₀, то она непрерывна в точке х₀ и, следовательно, u0. Поэтому и (u)→0, при х→0. Получаем

Т.е. существует ич.т.д.

Пример. (Вводим цепочку вспомогательных функций)

1)

2) у=sin lnx 3)y=

Пример. Дифференцирование степенной функции.

Покажем, что

х^α==e^αlnx

= e^αlnx=x^α·α·=αx^α-1 ч.т.д.

Производная степенно-показательной функции у=f(x)^g(x).

Рассмотрим логарифмическую производную, т.е. производную логарифмической функции:(относительная скорость изменения функции или темп изменения функции).

Тогда ln y=g(x)lnf(x). Дифференцируя, получим

.

Т.к. у=f(x)^g(x), получаем

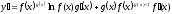
Т.е. для того, чтобы найти производную степенно-показательной функции надо сначала дифференцировать ее как степенную, а потом как показательную функцию и полученные результаты сложить.

Пример. Найти производную функции у=х^х.