- •Задание на выполнение курсовой работы
- •Цель, оформление и защита курсовой работы
- •Задание для выполнения
- •Форматирование данных в электронных таблицах
- •Применение итоговых функций
- •Построение диаграмм
- •Построение графиков алгебраических зависимостей
- •Решение уравнений методом подбора параметров
- •Решение задач оптимизации методом поиска решения
- •Работа с базами данных
- •Работа с матрицами
- •Построение имитационных моделей экономических систем
- •Модель условного города (динамика жилфонда)
- •Паутинообразная модель (модель микроэкономики)
Построение имитационных моделей экономических систем
Модель условного города (динамика жилфонда)
Рассмотрим условный город, в котором нас интересует обеспеченность жителей жильем.
Состояние системы (города) задается следующими компонентами:
R(t) – количество жителей города в момент времени t (предполагается, что рождаемость уравнивается смертностью)
S(t) – количество жилья в начале t-го года.
Y(t) – количество строительных рабочих в начале t-го года
Цель:
проследить динамику жилфонда
![]() .
.
Управляющие компоненты модели.
Предполагается, что коренное население не хочет работать на стройке, тогда:
Z(t) – количество ввезенных в город рабочих
K(t) – доля населения (в %), переквалифицированная в рабочих.
Параметры модели:
А – производительность одного рабочего
В1 – доля жилфонда, которая исчезает (выбывает) за год, ремонт не предусмотрен.
В2 – коэффициент выбытия строительных рабочих
Чтобы построить модель города и проводить на ней эксперименты, необходимо задать начальные условия R(0), S(0), Y(0).
Рекуррентные отношения (математическая модель динамики жилфонда города):
![]() -
численность населения в следующий год
-
численность населения в следующий год
![]() -
количество жилья в следующий год
-
количество жилья в следующий год
![]() -
количество строительных рабочих
-
количество строительных рабочих
* (R(t)-Y(t)) – количество не строительных рабочих, которых нужно обучить.
Таблица 1. Начальные значения параметров модели:
|
Управляющие параметры |
|
|
|
Обучение населения строительным специальностям |
K |
0,62% |
|
Ежегодный ввоз строительных рабочих |
z |
0% |
|
Параметры |
|
|
|
Производительность труда строительных рабочих |
A |
6 |
|
Коэффициент выбытия жилого фонда |
B1 |
10% |
|
Коэффициент выбытия строительных рабочих |
B2 |
10% |
Таблица 2. Начальные данные (момент времени t=0)
|
Номер года |
Обучение населения строительным специальностям, k |
Жилой фонд, S(0) |
Население города, R(0) |
Количество строительных рабочих к началу года, Y(0) |
Обеспеченность жильем, S/R |
|
0 |
0,62 |
125,00 |
65,00 |
0,00 |
1,92 |
Порядок выполнения задания
Разработка имитационной модели
Заполнить таблицу 2, используя начальные данные и рекуррентные отношения. Размерность таблицы – 200 строк (лет)
Построить графики значений Y и S/R на одной диаграмме
Построить графики значений R и S на одной диаграмме
Проведение имитационных экспериментов
Цель экспериментов - выбор управляющих переменных K(t), Z(t) с таким расчетом, чтобы к 10 году выйти на некоторый уровень обеспеченности жильем, а затем сменить управление так, чтобы оставаться на этом уровне и дальше
Изменяя управляющие параметры, наблюдать изменение величин R, S, Y и S/R. Добиться различных типов графиков
Анализ результатов, выводы
Паутинообразная модель (модель микроэкономики)
1. Постановка задачи детерминированной паутинообразной модели:
Спрос
–
линейная функция вида![]()
Предложение
–
линейная функция вида
![]()
Цена
при условии равновесия спроса и
предложения определяется из условия![]() :
:
![]()
Цель – исследовать поведение рыночной цены при различных параметрах линии спроса и предложения
2. Начальные условия:
|
a |
b |
c |
f |
P(0) |
|
54 |
5 |
8 |
4 |
10 |
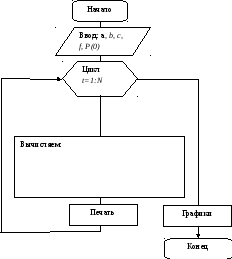
3. Вычислить значение P(t) для 20 значений t, t(0)=0
4. Вычислить значения D(t) для всех значений t
5. Вычислить значения S(t) для всех значений t
6. Построить графики рассчитанных величин
7. Провести эксперименты, изменяя соотношение коэффициентов наклона прямых спроса и предложения
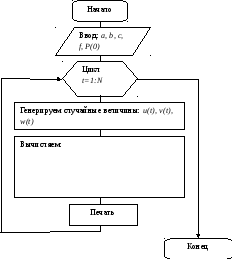
1. Постановка задачи стохастической паутинообразной модели:
Спрос
–
линейная функция вида
![]()
Предложение
–
линейная функция вида
![]()
Цена
при условии равновесия спроса и
предложения определяется из условия
![]() :
:
![]()
2. Начальные условия:
|
a |
b |
c |
f |
P(0) |
|
54 |
5 |
8 |
4 |
10 |
3. Вычислить значение P(t) для 20 значений t, t(0)=0
4. Вычислить значения D(t) для всех значений t
5. Вычислить значения S(t) для всех значений t
6. Построить графики рассчитанных величин
7. Провести эксперименты, изменяя соотношение коэффициентов наклона прямых спроса и предложения