1.3. Средние значения физических величин

Продолжим рассмотрение основных положений ТВ, акцентируя внимание на термодинамических процессах. Из-за беспорядочности движения система молекул за большой промежуток времени проходит через многочисленный ряд состояний, в каждом из которых она побывает не один, а много раз. Пусть состояние газа характеризуется некоторой величиной а, которая принимает дискретный ряд значений (число молекул в выделенном объеме). Проделаем (мысленно) множество наблюдений над системой в ее различных состояниях. Окажется, что в N₁ наблюдениях из N система имеет значение а₁, в N₂ - значение а₂ и т.д. Среднее значение (арифметическое) дискретной физической величины определяют по формуле

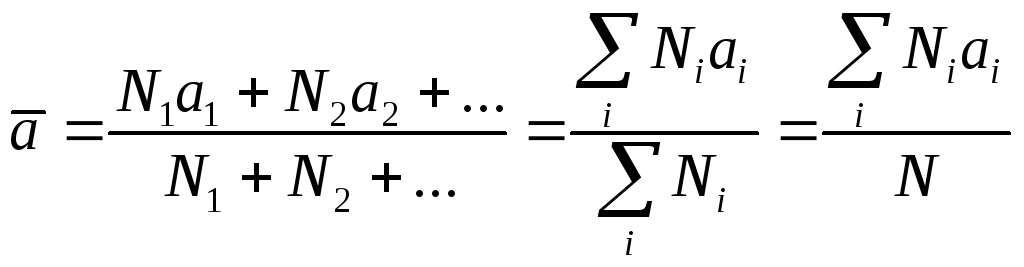
(7),

или, с учетом (1), запишем

(7^/).

Бытовой пример. В группе из 19 человек 3 человека 17-ти летних, 10 человек 18-ти летних, и шестеро 19-ти летних. Средний возраст студентов в группе: а_ср= (3^.17 + 10^.18 +6^.19)/19 = 18,16 лет.

В том случае, когда величина N_i близка к единице, можно воспользоваться более простой формулой для нахождения среднего значения

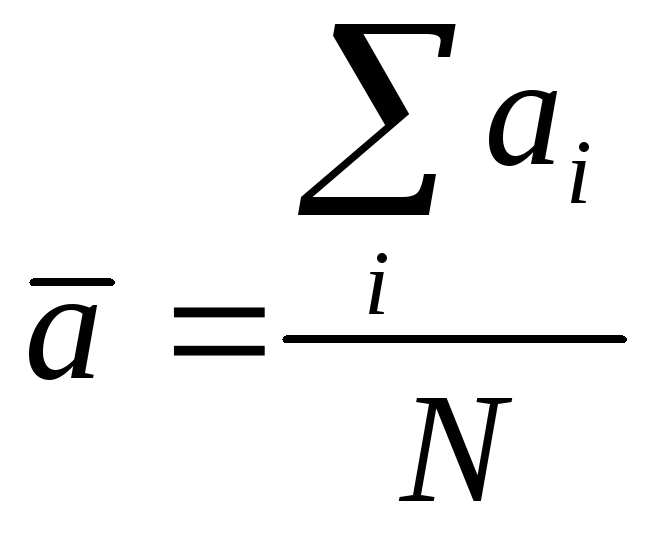
(7^//),

где i – полное число испытаний от 1 до N.

Покажем, как поступать с величиной x, принимающей в определенном интервале непрерывный ряд значений (скорость молекул), число которых бесконечно велико. В этом случае вероятность, определяемая формулой 1, теряет смысл, поскольку в состоянии с фиксированным значением x, система проводит бесконечно малое время, и соответствующая вероятность оказывается практически равной нулю. Следует рассматривать вероятность того, что данная величина лежит в интервале от x до x + dx. Время, которое система проводит в состояниях из выбранного интервала, пропорционально ширине интервала dx. Тогда вероятность того, что данная величина находится в пределах от x до x + dx, равна

dP_x = (x)dx (8),

где (x) – плотность вероятности или вероятность, отнесенная к ширине интервала dx. Тогда среднее значение непрерывно меняющейся величины (подобно 7^/) будет

(9),

здесь интегрирование ведется по всем возможным значениям x. По аналогии определяют среднее квадратичные значения дискретной a и непрерывной x величин:

(10),

(11).

4. Средняя квадратичная флуктуация

Важно также знать, насколько велики отклонения рассматриваемой величины от ее среднего значения. Воспользоваться для оценки отклонением а = а_i - а_ср (линейной флуктуацией) не удается, поскольку отклонения от а_ср в большую и меньшую стороны происходят одинаково часто, и в среднем а оказывается равным нулю. Используя правила вычисления средних величин, находим

Для того, чтобы отклонения не “гасили” друг друга, в качестве меры отклонения используют квадрат величины а. Воспользуемся выражением (10) и введем среднюю квадратичную флуктуацию величины а

(12),

которую называют также дисперсией и обозначают ², то есть:

(12^/).

Дисперсия служит мерой разброса данной величины (а), она тем больше, чем больше вероятность отклонения величины (а_i) от среднего. Линейной мерой разброса служит корень квадратный из дисперсии или среднеквадратичное отклонение (величины а от ее среднего арифметического значения)

(13).

Погрешность, которую мы совершаем, заменив а на а_ср, оценивают с помощью относительной флуктуации а

(14).

Основные свойства дисперсии или квадрата среднеквадратичного отклонения:

а) дисперсия независимых величин равна сумме их дисперсий (без доказательства);

б) дисперсия величины а равна среднеквадратичному минус квадрат среднего этой величины, используя формулу (10) получим

или окончательно математическая запись свойства б):

(15).

Применим полученные формулы к объему с газом. Среднее число молекул в выделенном объеме V составит

(16),

здесь N –полное число молекул в объеме V, n - концентрация молекул газа. Найдем отклонение от среднего или дисперсию числа молекул в объеме V.

Сопоставим каждой молекуле случайную величинуа, которая принимает значения а = 1, если молекула в объеме V, и а = 0, если молекула вне этого объема. Тогда согласно (10) среднеквадратичное значение а будет

,

асреднее значение составит: . Найдем дисперсию с помощью формулы 15:

Дисперсия  общего числа частиц в объеме V с учетом свойства а) составит

(17)*.