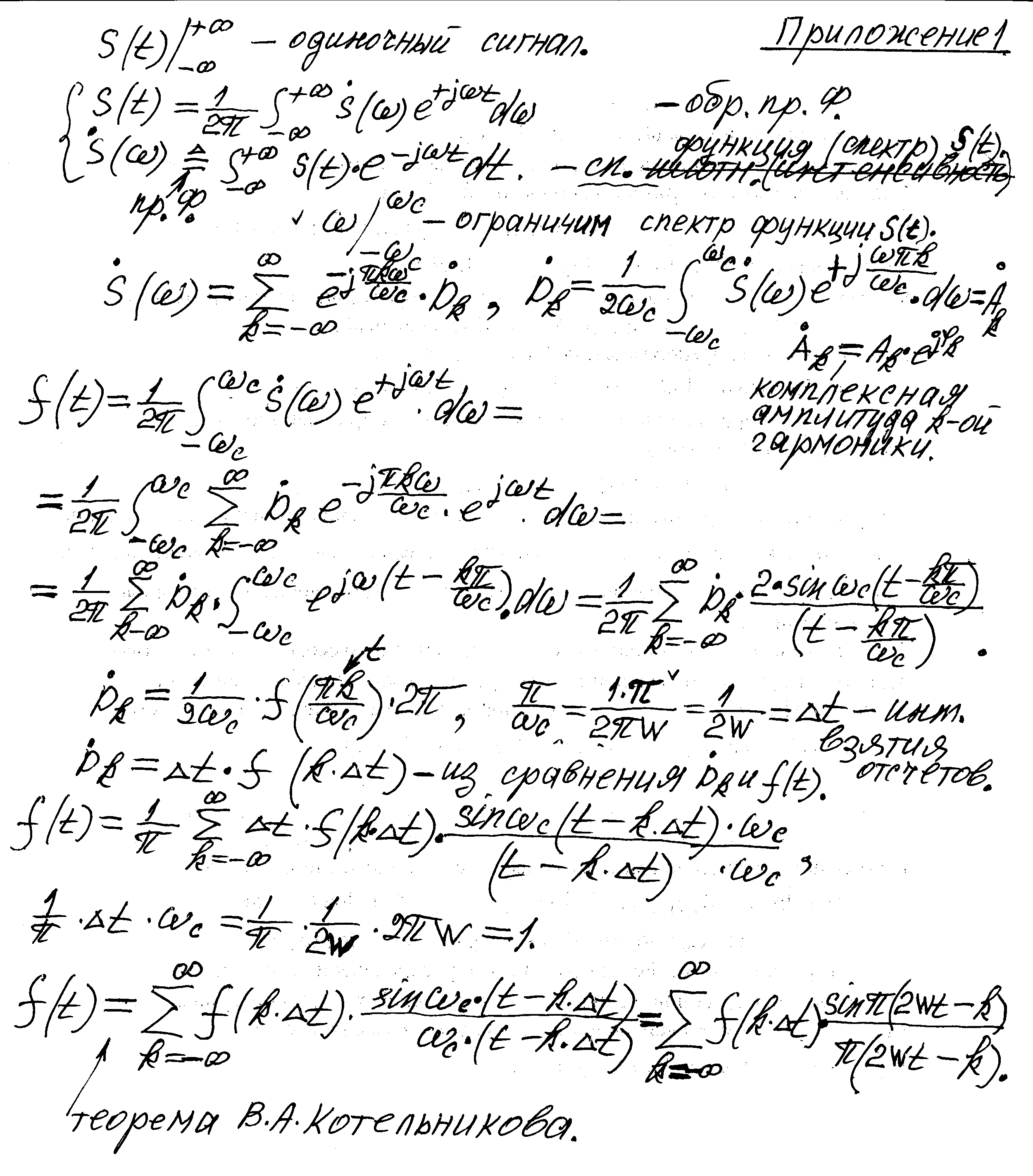Лекция 2,3

Информация для непрерывных величин

1.Cтационарный случайный процесс не зависит от момента отсчёта времени, т.е.

плотн. вер. p(x₂) = p(x₁), корреляц. ф-ия k(t_i , t_j) = k(t_j – t_i) = k(τ) _.

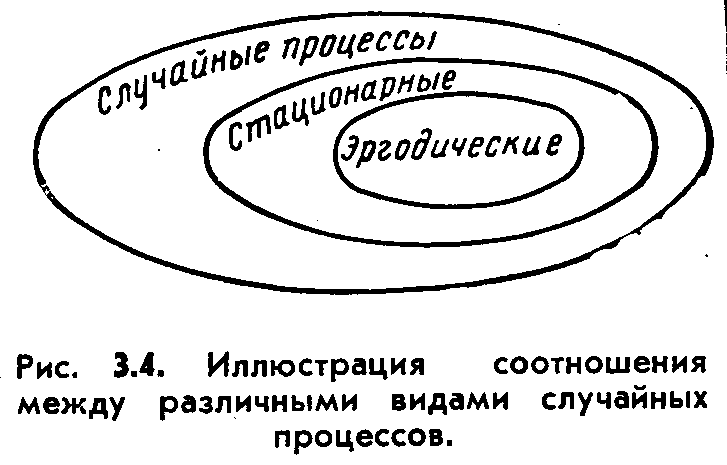
2 . Все рассматриваемые случайные процессы обладают свойством эргодич -

ности: cреднее значение по времени равно среднему значению по ансамблю

функций, т.е. T T

x(t) = lim 1/T·∫₀ x(t)·dt, T→∞; k(τ) = lim (1/T)·∫₀ x(t)·x(t +τ)·dt, T→∞ .

Оказывается, что для большинства случайных процессов, являющихся стацио- нарными в узком смысле, указанные характеристики можно получить путём усреднения соответствующих величин для одной реализации за достаточно боль - шой промежуток времени.

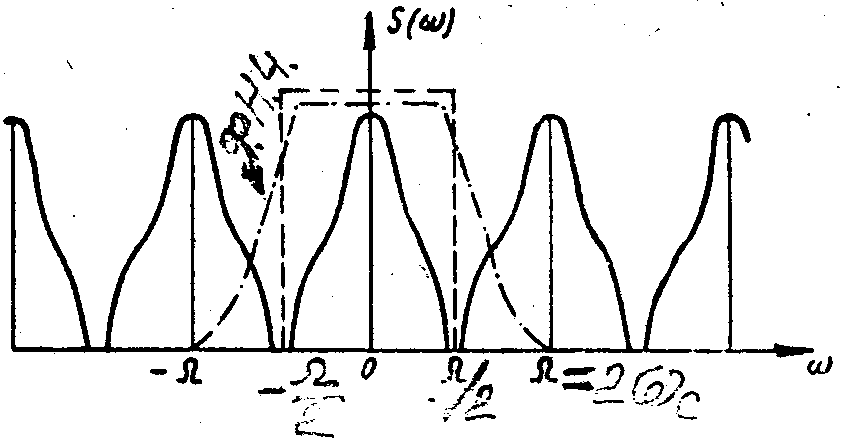
(c периодом разложения спектр.функции S(ω) по частоте 2ω_c = 4πW, рис.5.2).

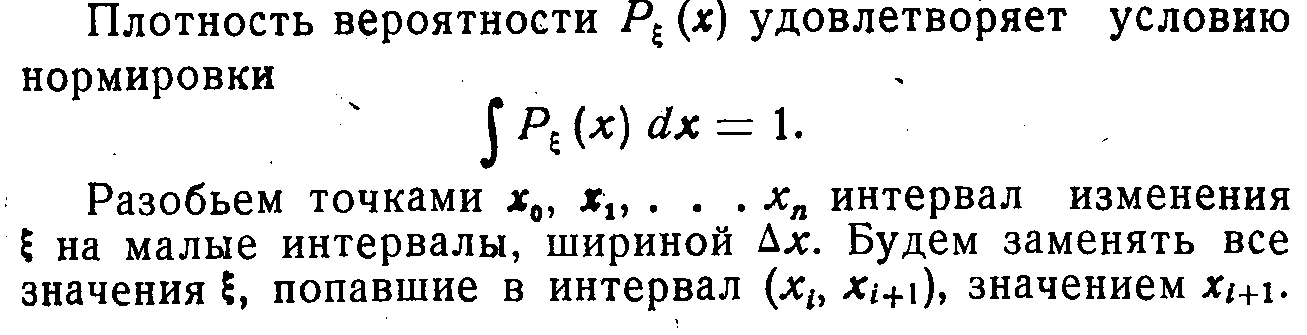
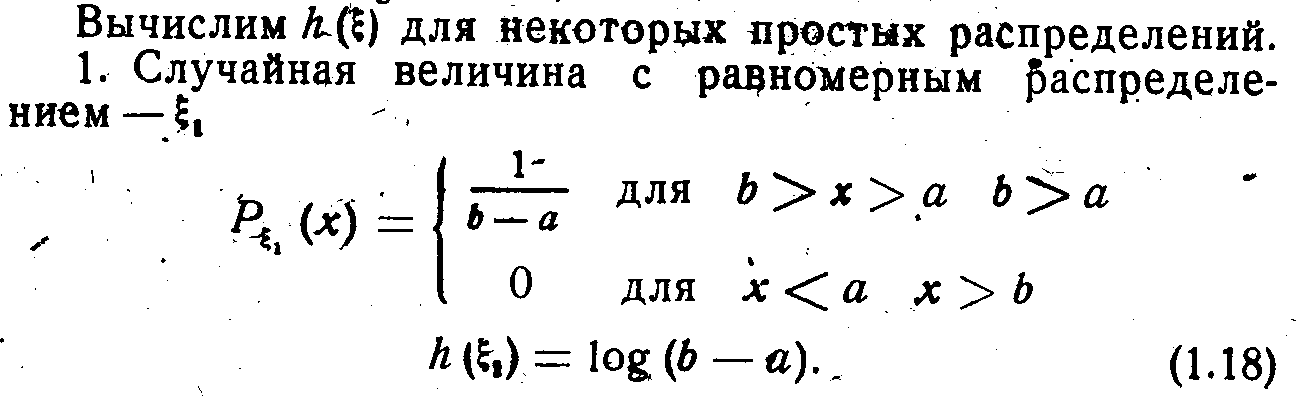
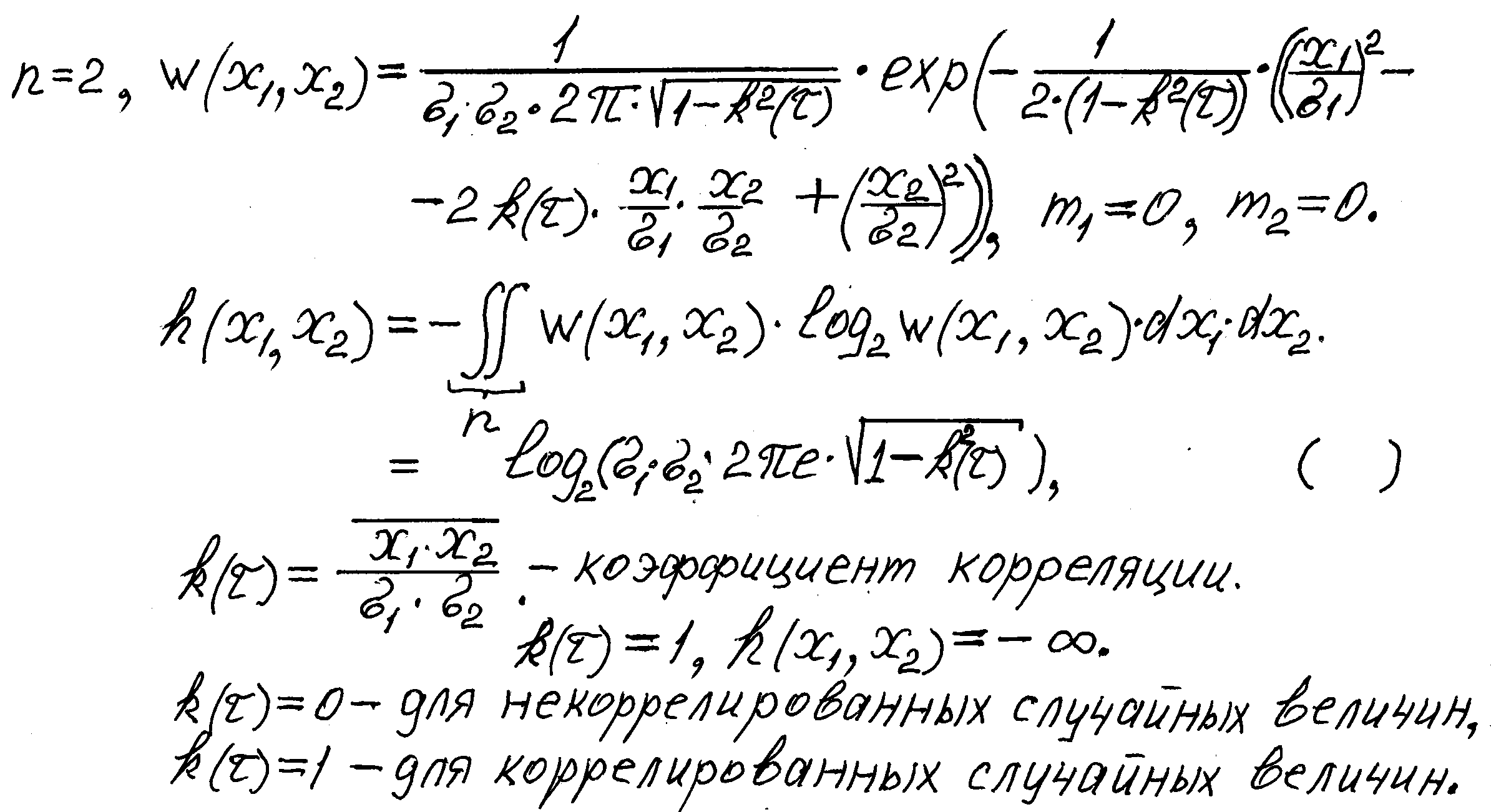
детерминированная линейная зависимость

1.Из всех непрерывных случайных величин, заданных на интервале (а,b), (а< х < b), наибольшей дифференциальной энтропией log(b - a) обладает cлучайная величина х с равномерным распределением p(x) = 1/(b – a).

2. Из всех случайных величин с заданной дисперсией σ² = M (x - a)²

(M- знак математического ожидания) наибольшей дифференциальной энтропией

log (σ · √2πe ) обладает случайная величина х с нормальным распределением (доказывается методом вариационного исчисления).

Аналогичным образом в n - мерном случае предположим, что моменты второго порядка плотности вероятности p(x1,……, xn) фиксированы и равны Aij:

____

Aij = ∫…..∫ xi· xj· p (x1,……, xn) · dx1,……., dxn= xi· xj.

При помощи аналогичных вычислений находим, что максимум энтропии имеет место, когда p (x1,……, xn) является n – мерным нормальным распределением с моментами второго порядка Aij.

3. Если распределение x ограничено положительной полуосью

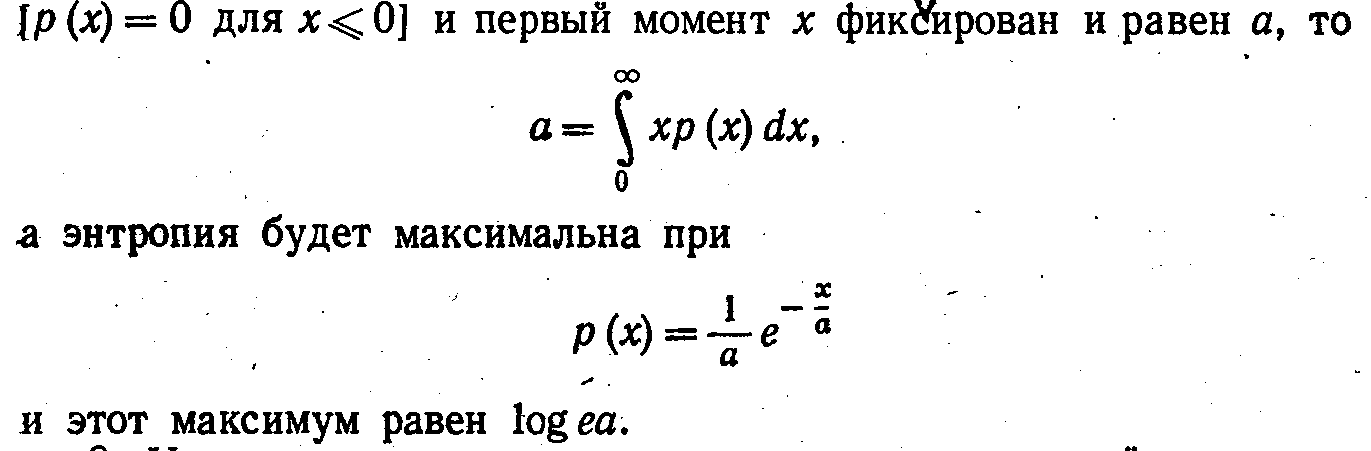
4. Дифференциальная энтропия совокупности случайных величин.

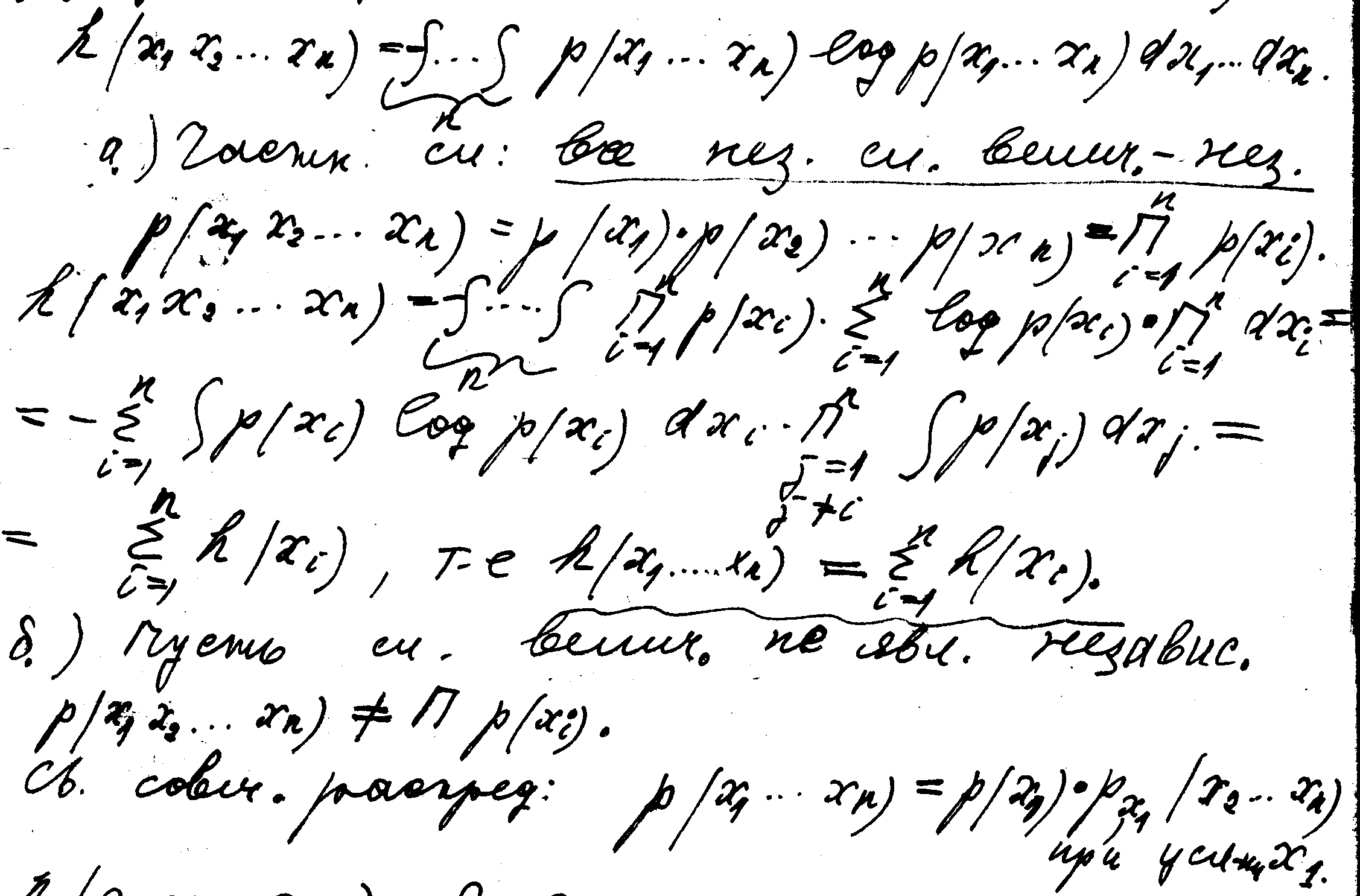
Тогда после подстановки

h(x₁,x₂,…..,x_n) = h(x₁) + h_x1 (x₂,x₃,……..,x_n) = h(x₁) + h_x1(x₂) + h_x1x2(x₃,x₄,……,x_n) = h(x₁) + h_x1(x₂) + h_x1x2 (x₃) + ….. + h_{x1x2……x n-1}(x_n) ≤

h(x₁) + h(x₂) + h(x₃) + ……….+ h(x_n). ( ) Это–обобщённое правило свойства аддитивности; здесь h_x1(x₂) ≤ h(x₂) и т.д. Для 2-х случайных величин: h(x₁,x₂) = h(x₁) + h_x1(x₂) = h(x₂) + h_x2 (x₁) ≤ h(x₁) + h(x₂).

(неопределён-ть опыта может лишь уменьш-ся при знании результатов др. опыта).

5. Имеется одно важное различие между энтропией непрерывных и дискретных величин. В дискретном случае энтропия изме –

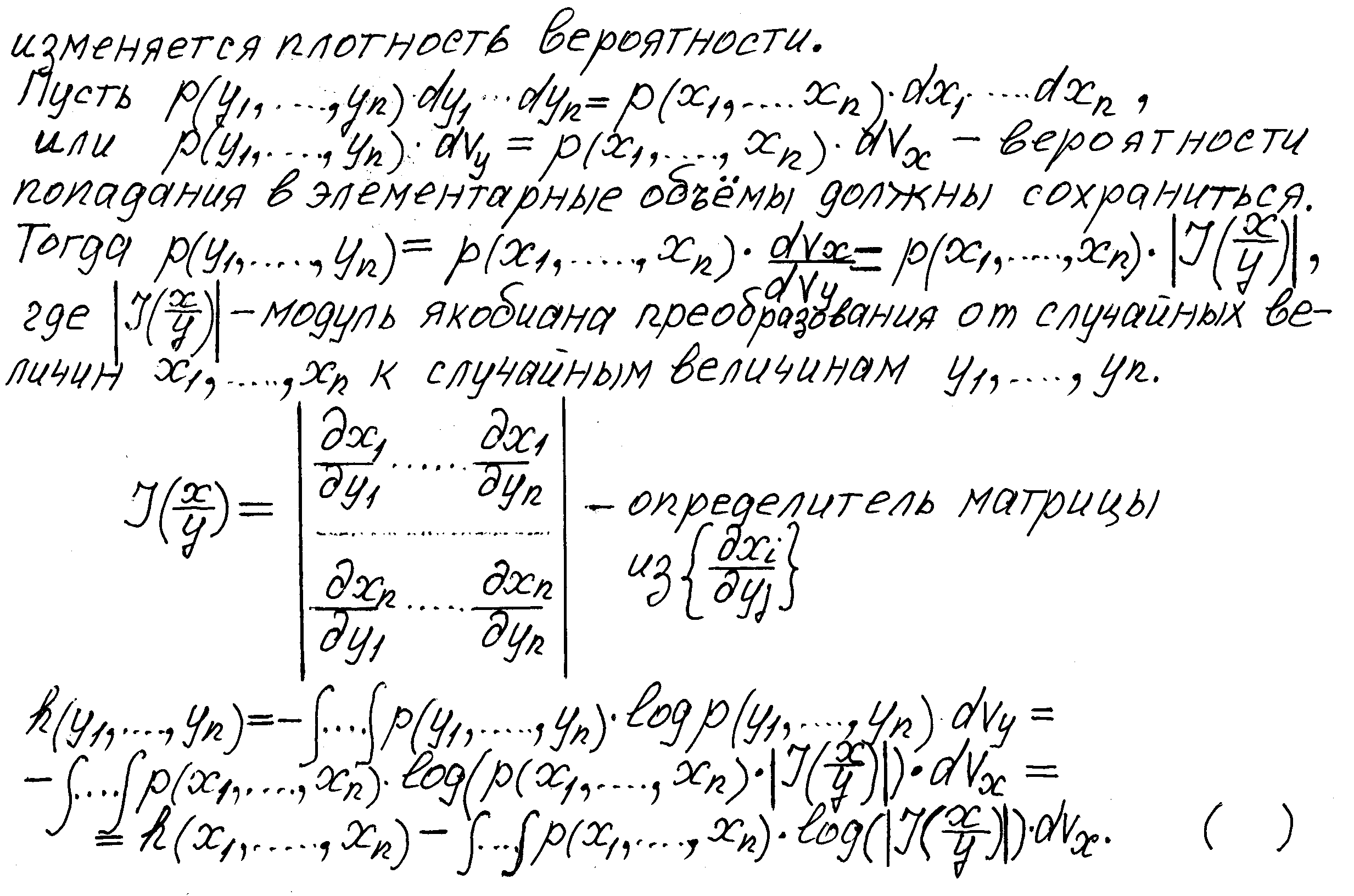
Пример. Рассмотрим линейное преобразование вида y = ax +b.

Обратное преобразование x = (y-b)/a; якобиан преобразования I(x/y) = dx/dy =1/a,

p(y) = p(x)·1/a. h(y) = - ∫p(y)·log p(y)·dy = - ∫p(x) ·log ( p(x) ·1/a) ·dx = h(x) + log a,

где ∫p(x)·dx =1. Дифференциальная энтропия линейного преобразования не зави - сит от сдвига b.

Дифференциальная энтропия не меняется,если повернуть вектор (или систему координат) таким образом, что его длина не меняется; I(x/y) = 1, h(y) = h (x).

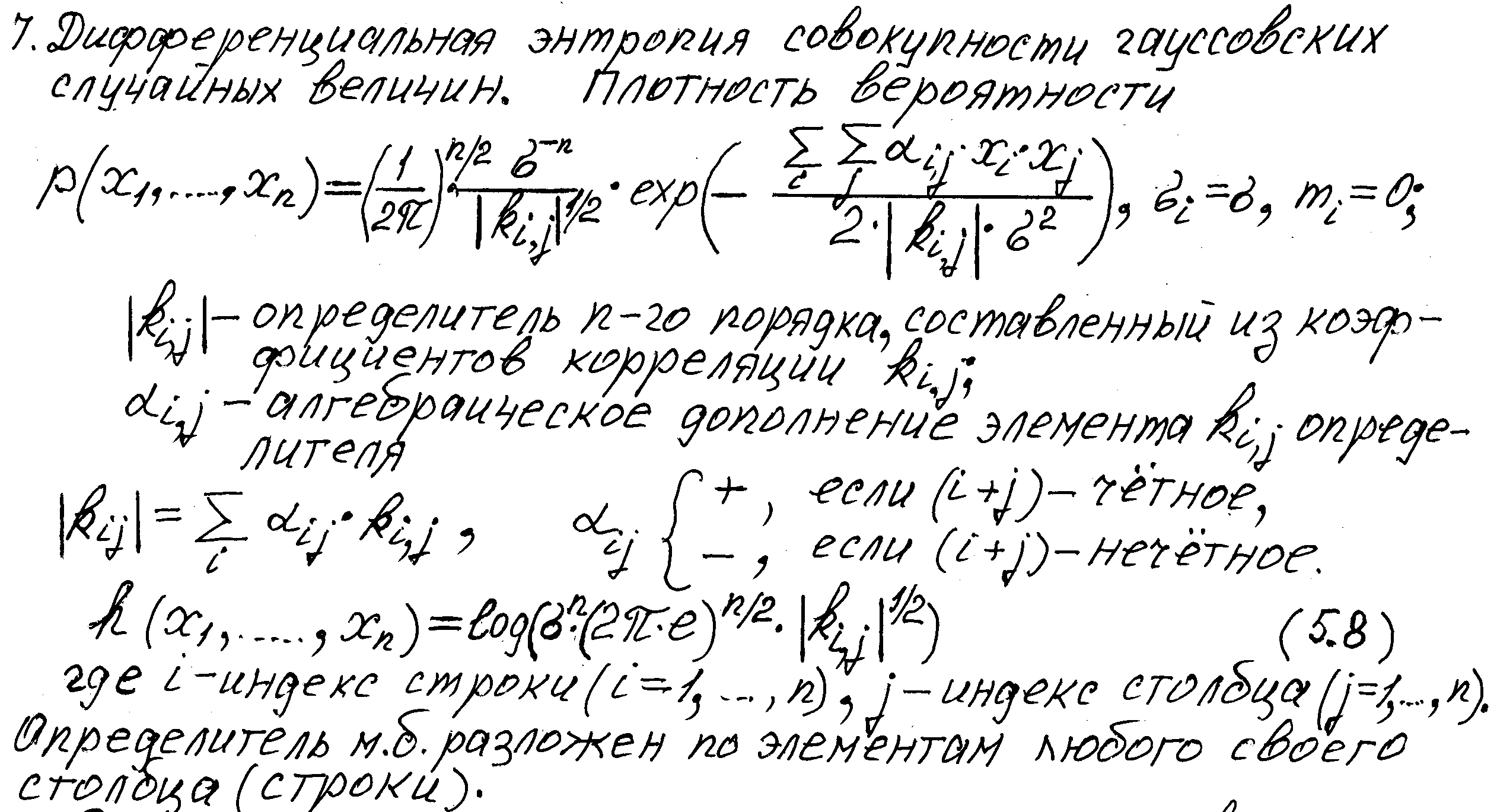
Корреляционная теория даёт полное описание нормальных процессов.

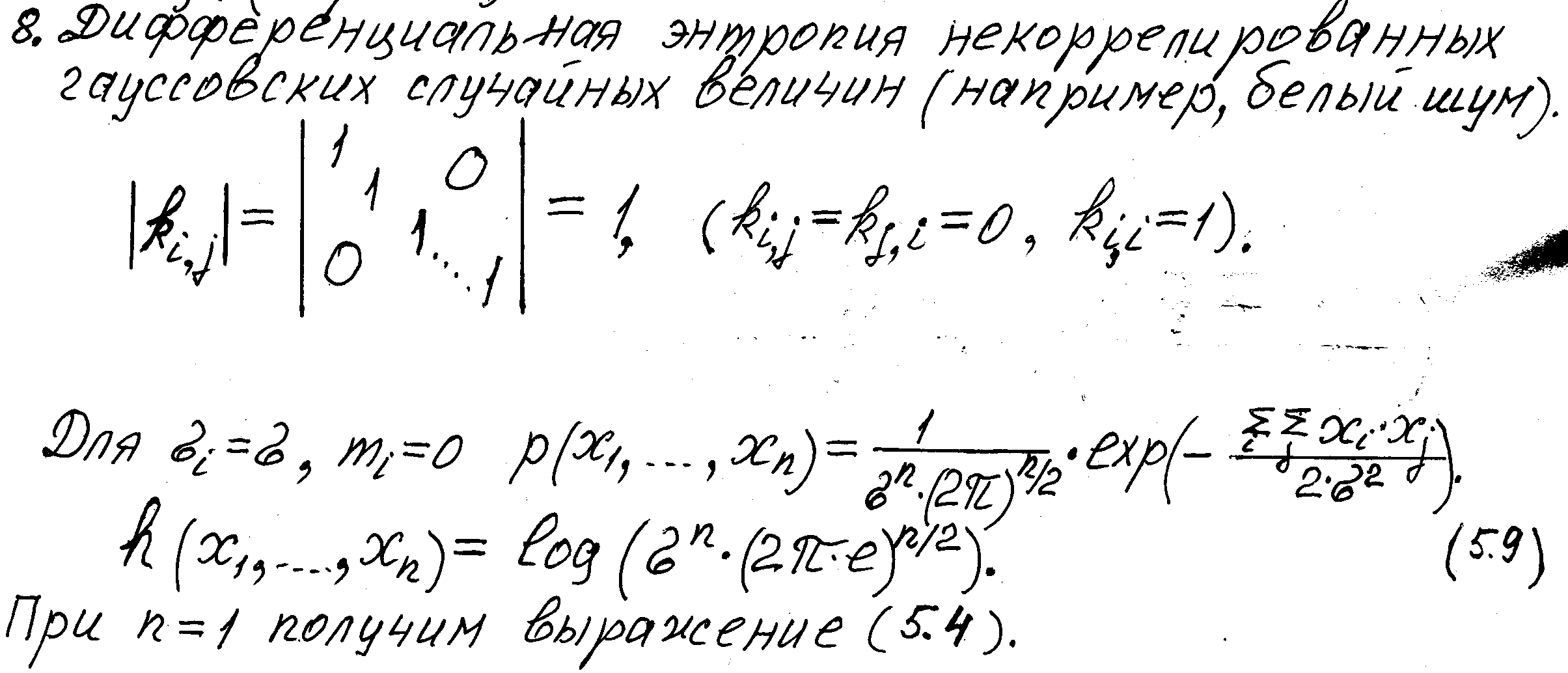
Энтропийная мощность

Пусть Н' = ln(√2πeN₁) - энтропия ансамбля.

N₁≤ N.

Cреднее

Количество взаимной информации для непрерывных величин

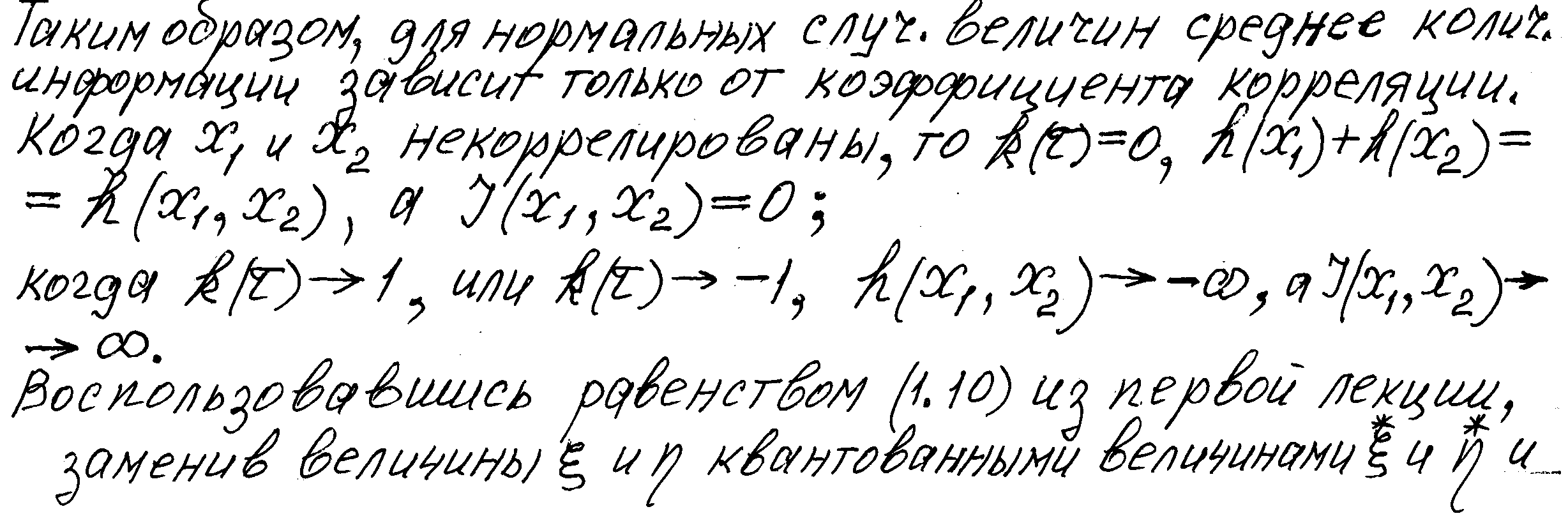
перейдя к пределу, найдём среднее количество взаимной информации двух случайных величин в виде :

I(ξ , η) = ∫∫ p(x, y) · log _p(x,y)_ dx·dy = R, ( 5.12 )

p(x)·p(y)

или скорость передачи R= I(ξ , η)/T.

Свойства среднего количества взаимной информации для непрерывных

величин

1) I(x, y) ≥ 0 , т.к. условная дифференциальная энтропия равна или меньше безусловной. I(x,y) = 0 только, если x и y независимы.

2) Свойство аддитивности:

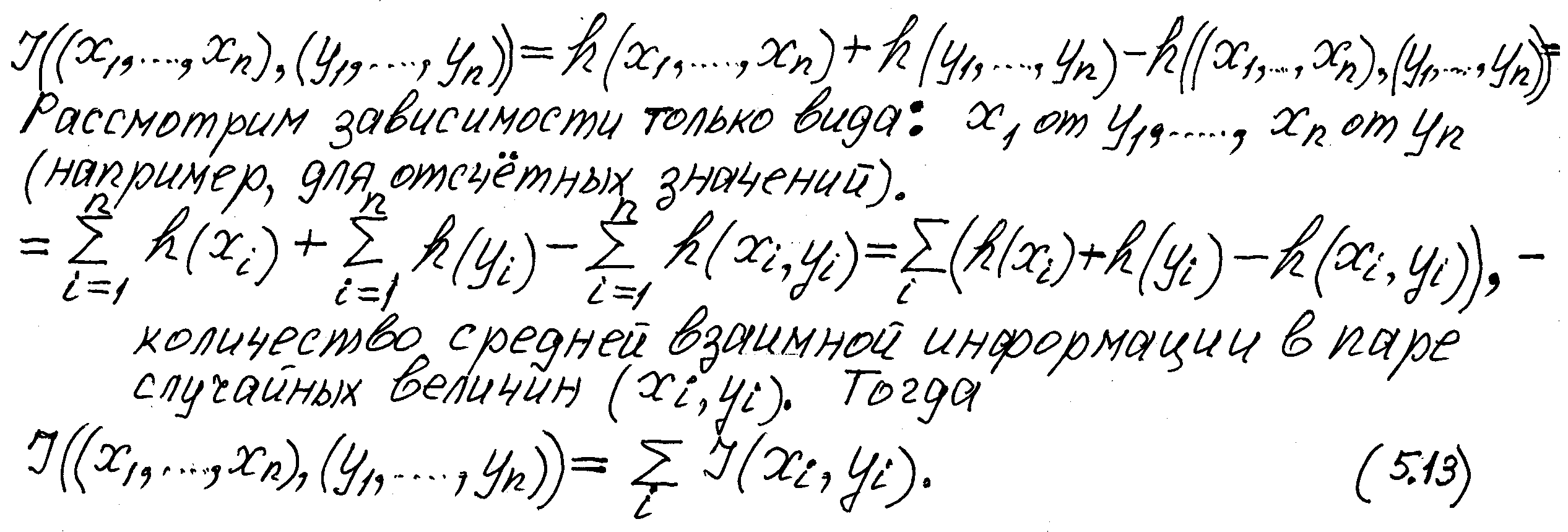
3) I(x, x) = → ∞ ( ср.c I(A,A) = H(A) – H_A(A) = H(A) для дискретных величин).

12