
Лабы / Разработки / Labs1
.rtfЛабораторная работа 1
Численные методы минимизации функций одной переменной
Будем рассматривать задачу минимизации функции одной переменной
на отрезке:

Предполагается,
что целевая функция
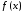 является унимодальной на отрезке
является унимодальной на отрезке
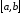 .
.
В
данной работе изучаются основные методы
численного нахождения
 :
:
метод деления отрезка пополам и метод золотого сечения.
Метод деления отрезка пополам
Основная
идея:
пусть
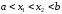 .
Сравнив значения
.
Сравнив значения
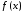 в точках
в точках
 и
и
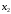 (пробных точках), можно сократить отрезок
поиска точки минимума
(пробных точках), можно сократить отрезок
поиска точки минимума
 ,
перейдя к отрезку
,
перейдя к отрезку
 ,
если
,
если
 ,
или к отрезку
,
или к отрезку
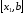 ,
если
,
если
 .
Описанную процедуру можно повторить
необходимое число раз, последовательно
уменьшая отрезок, содержащий точку
минимума. Когда длина последнего отрезка
станет достаточно малой следует выбрать
середину этого отрезка в качестве
.
Описанную процедуру можно повторить
необходимое число раз, последовательно
уменьшая отрезок, содержащий точку
минимума. Когда длина последнего отрезка
станет достаточно малой следует выбрать
середину этого отрезка в качестве
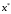 .
.
Алгоритм:
пусть
 требуемая точность определения
требуемая точность определения
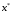 .
.
1.
Выбирать
 и
и
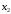 по следующим формулам
по следующим формулам

Здесь
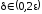 .
Вычислить
.
Вычислить
 и
и
 .
.
2.
Сравнить
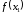 и
и
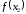 .
Если
.
Если
 ,
то перейти
,
то перейти
к
отрезку
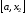 ,
положив
,
положив
 ,
иначе к отрезку
,
иначе к отрезку
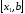 ,
,
положив
 .
.
Вопрос: Во сколько раз уменьшается отрезок? Остается ли т. минимума на
выбранном отрезке?
3.
Найти достигнутую погрешность
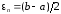 .
Если
.
Если
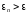 ,
то перейти к следующей итерации,
вернувшись к пункту 1, в противном
,
то перейти к следующей итерации,
вернувшись к пункту 1, в противном
случае
завершить поиск
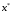 .
.
4.
Положить
 .
Найти
.
Найти
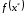 .
.
Дополнительно
можно посмотреть зависимость n
от
 ,
где n
число итераций.
,
где n
число итераций.
Метод золотого сечения
Основная
идея: Рассмотрим
такое симметричное расположение точек
 и
и
 на отрезке
на отрезке
 ,
при котором одна из них становится
пробной точкой и на новом отрезке,
,
при котором одна из них становится
пробной точкой и на новом отрезке,
полученном
после исключения части исходного
отрезка. Использование таких точек
позволяет на каждой итерации метода
исключения отрезков, кроме первой,
ограничится определением только одного
значения
 ,
так как другое значение уже найдено на
одной из предыдущих итераций.
,
так как другое значение уже найдено на
одной из предыдущих итераций.
Общие сведения:
Для
отрезка
 выражения для пробных точек имеют вид
выражения для пробных точек имеют вид

Точки
 и
и
 обладают следующим свойством: каждая
из них делит отрезок
обладают следующим свойством: каждая
из них делит отрезок
 на две неравные части так, что отношение
длины отрезка к длине его большей части
равно отношению длин большей и меньшей
частей отрезка (точки золотого сечения).
на две неравные части так, что отношение
длины отрезка к длине его большей части
равно отношению длин большей и меньшей
частей отрезка (точки золотого сечения).
Справедливы
соотношения
 и
и
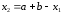 .
Поэтому
.
Поэтому
на каждой итерации пробную точку нового отрезка можно найти по перешедшей на него точке.
Вопрос:
Во сколько раз
 уменьшается отрезок на k-ой
итерации?
уменьшается отрезок на k-ой
итерации?
Алгоритм:
1. Найти
 и
и
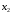 по формулам. Вычислить
по формулам. Вычислить
 и
и
 .
Положить
.
Положить
 ,
,
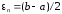 .
.
2.
Проверка на окончание поиска : если
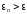 ,
то перейти к 3, иначе к
,
то перейти к 3, иначе к
п. 4.
3.
Переход к новому отрезку и новым пробным
точкам. Если
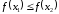 ,
,
то
положить
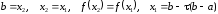 и вычислить
и вычислить
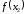 .
Положить
.
Положить
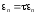 и перейти к шагу 2.
и перейти к шагу 2.
Случай
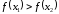 разобрать самостоятельно.
разобрать самостоятельно.
4.
 ,
,
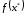
Дополнительно
можно посмотреть зависимость n
от
 ,
где n
число итераций. Сравнить с методом
деления отрезка пополам
,
где n
число итераций. Сравнить с методом
деления отрезка пополам
