Лабы / Разработки / Labs4

Лабораторная работа 4

Методы минимизации, не использующие дифференцируемость целевой функции

В работе рассматривается метод Нелдера – Мида.

Общие сведения: Напомним, что симплексом в Rⁿ называется выпуклая оболочка n+1 точек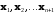, не лежащих в одной n-1 – мерной плоскости. Пусть требуется определить минимум целевой функции 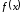. Алгоритм метода Нелдера – Мида решения этой задачи заключается в следующем. На каждой итерации сравниваются значения 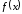в вершинах симплекса. Затем преобразуется та вершина (без ограничения общности --- ) симплекса в которой достигается максимальное значение 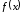. Положение новой вершины определяется сравнением значений функции в четырех пробных точках

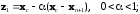
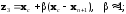
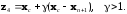
Здесь --- центр тяжести остальных n вершин симплекса ().

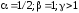Среди выбирается точка, где 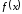минимальна. Итерационный процесс продолжают до тех пор, когда либо разность между значениями функции в вершинах симплекса, либо разность между значениями функции в вершинах симплекса становится достаточно малой.

Начальный симплекс можно выбрать правильным если известна, то

, (*)

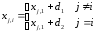где .

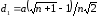
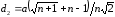Алгоритм: 1. Выбрать параметры 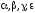начальную точку и длину ребра a

правильного симплекса. Начальный симплекс определить по

формулам (*).

2. Вычислить значения функции в точках .

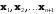3. Упорядочить вершины так, чтобы .

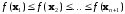4. Проверить достижение заданной точности. Если оно выполнено, то

. Иначе перейти к п. 5.

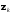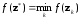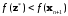5. Найти и определить . Если , то

положить 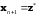и перейти к п.3. Иначе к п.6.

6. Уменьшить симплекс, полагая 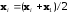и перейти к п.2.

Дополнительно: Используйте встроенную функцию fminsearch, реализующую метод

Нелдера-Мида [x,fval,exitflag,output] = fminsearch(@fun,x₀).

Сравните количество итераций и вычислений fun для данной функции

fminsearch и для написанной вами функции.