Лабы / Разработки / Labs5

Лабораторная работа 5

Методы нелинейного программирования при наличии ограничений

В работе рассматриваются методы штрафных функций и барьерных функций.

Метод штрафных функций

Задача нелинейного программирования 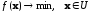сводится к последовательности задач безусловной минимизации

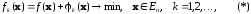
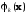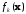В данном методе последовательность выбирается так, чтобы при больших k функция из (*) мало отличалась от 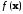при 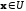и быстро возрастала при удалении точки 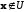от допустимого множества.

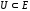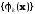Пусть ­ заданное множество. Последовательность функций , определенных в E и обладающих свойством

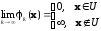
называется последовательностью штрафных функций множества U.

Если множество U задано неравенствами

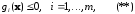
то часто полагают 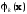=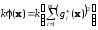, где

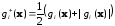
В качестве критерия останова можно использовать неравенство

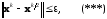
где 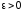, а k ­ четное число. При его выполнении полагают .

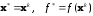Метод барьерных функций

Как и в методе штрафных функций задача минимизации 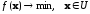сводится к последовательному решению задач (*), только последовательность 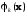выбирается по-другому.

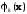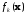Функции определяются таким образом, чтобы при больших k функция из (*) мало отличалась от 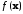при 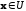и в то же время при приближении к границе допустимого множества U эти функции неограниченно возрастали. Таким образом, влияние барьерной функции 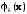при больших k состоит в создании «барьера» с крутыми склонами вдоль границы допустимого множества.

В общем случае последовательность барьерных функций определяется двумя условиями:

1) 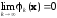для любой фиксированной ;

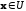2) 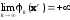для любой последовательности 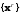внутренних точек множества U , сходящейся к какой-либо граничной точке этого множества.

В случае ограничений типа (**) барьерные функции часто выбирают в виде

=
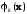