2. Эквивалентность формул

Две формулы иназываютсяэквивалентными(обозначается:если доказуемы секвенциииЗаметим, что символне принадлежит языку исчисления высказываний. Он принадлежитметаязыку, т.е. языку, на котором мы описываем исчисление высказываний.

Предложение 1. Отношение является отношением эквивалент-ности.

Доказательство. Рефлексивность и симметричность отношенияочевидны. Докажем его транзитивность. ПустьиТогдаТак какито по правилуАналогично получаемТаким образом,

Замечание. Впоследствии мы докажем, что эквивалентность формул означает, что эти формулы совпадают как булевы функции, у которых аргументами являются атомарные формулы. Но это будет сделано лишь после достаточного развития теории.

Предложение 2. Еслито для любой конечной последовательности формулдоказуемость секвенцииравносильна доказуемости секвенции

Доказательство получается непосредственным применением правила

Теорема 1 (о замене). Еслиито

Доказательство. Докажем утверждение о конъюнкции, предоставив доказательство других эквивалентностей читателю:

(1)		(дано);
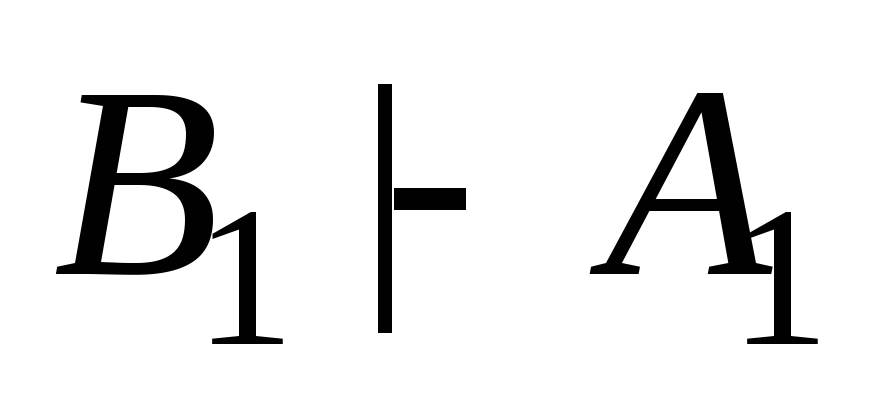
(2)		(дано);
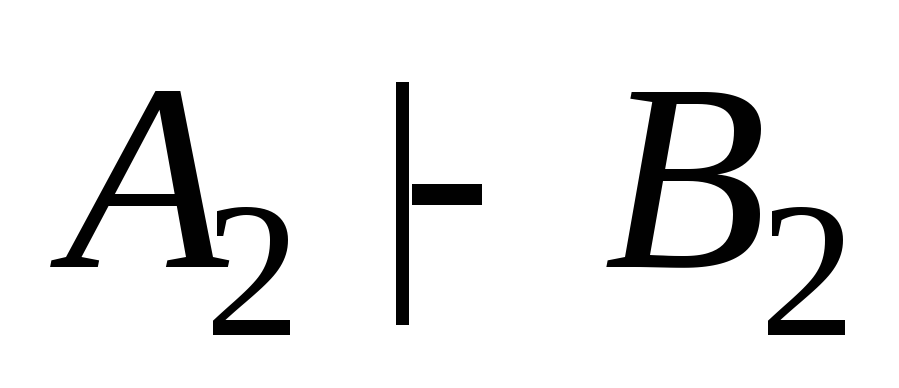
(3)		(дано);
(4)		(дано);
(5)		(аксиома);
(6)		(из (5) по правилу 3)
(7)		(из (5) по правилу 3);
(8)		(из (6) и (1) по правилу );
(9)		(из (7 и ((3)по правилу );
(10)		(из (8) и (9) по правилу 1).

Секвенция доказывается аналогичным образом.

Следствием этой теоремы является тот факт, что если то любое вхождение формулыв более сложную формулуможет быть заменено на формулупричём новая формула будет эквивалентна формулеДоказательство осуществляется индукцией по длине формулы

Приведём несколько примеров доказательства эквивалентности формул.

1. Докажем, что

   (1)		(аксиома);
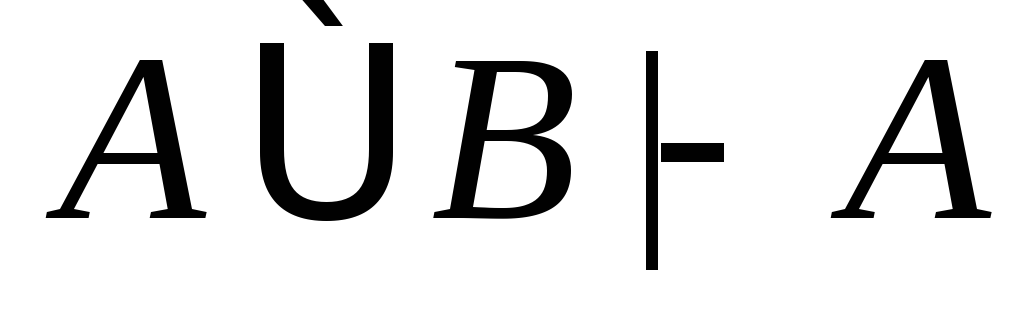
   (2)		(из (1) по правилу 2);
   (3)		(из (1) по правилу 3);
   (4)		(из (3) и (2) по правилу 1).

2. Докажем, что

(1)		(аксиома);
(2)		(из (1) по правилу 4).

В обратную сторону:

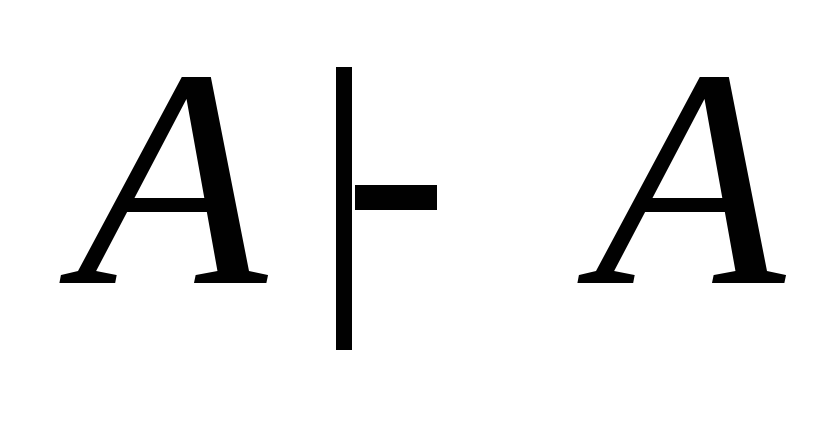
(1)		(аксиома);
(2)		(из (1) по правилам 11, 12);
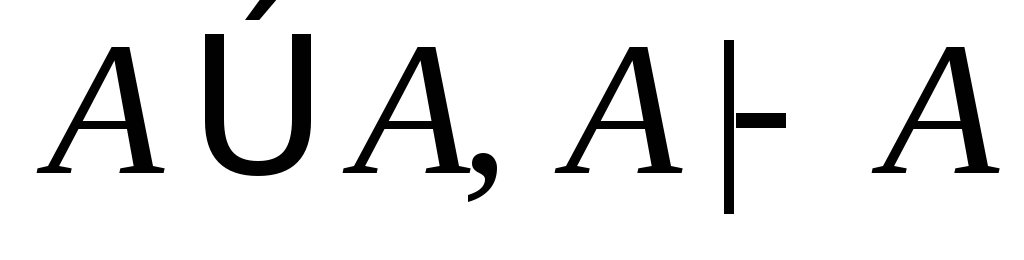
(3)		(то же самое);
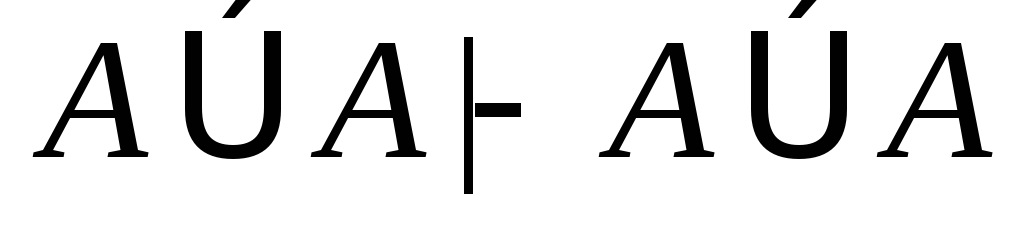
(4)		(аксиома);
(5)		(из (2), (3), (4) по правилу 6).

3. Докажем, что

(1)		(аксиома);
(2)		(аксиома);
(3)		(из (1) по правилу 12);
(4)		(из (2) по правилам 11, 12);
(5)		(из (3) и (4) по правилу 10);
(6)		(из (5) по правилу (е));
(7)		(аксиома);
(8)		(из (7) по правилам 11, 12);
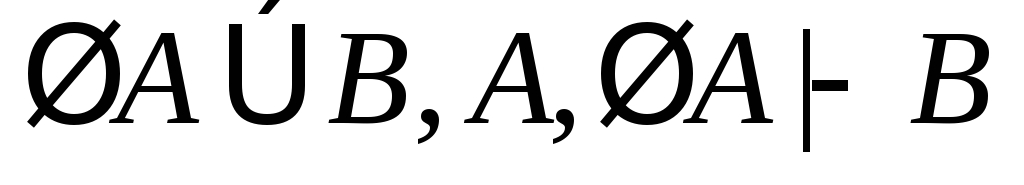
(9)		(из (6) по правилам 11, 12);
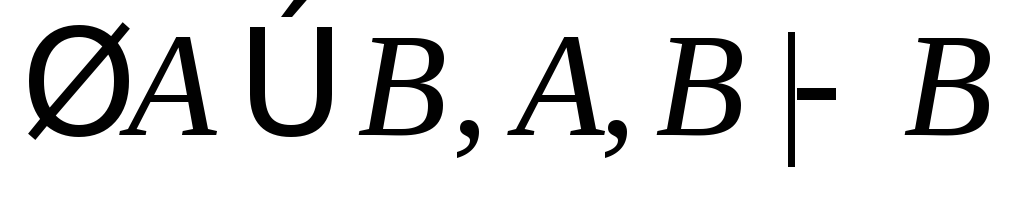
(10)		(из (7) по правилам 11, 12);
(11)		(аксиома);
(12)		(из (9), (10), (11) по правилу 6);
(13)		(из (12) по правилу 7).

В обратную сторону:

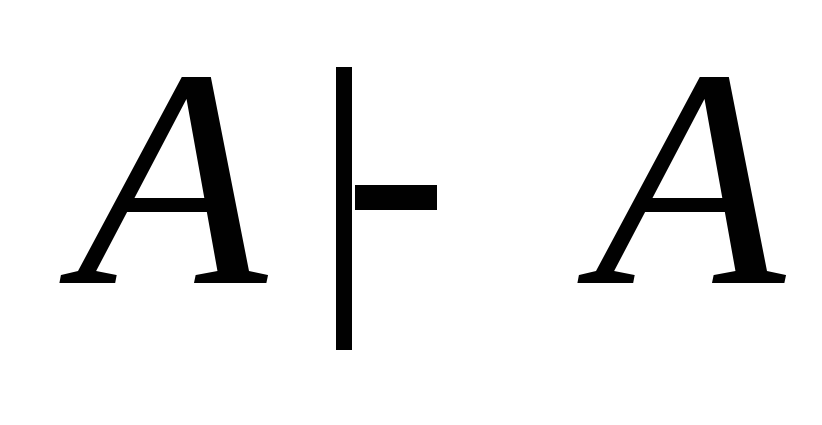
(1)		(аксиома);
(2)		(аксиома);
(3)		(из (1) по правилам 11, 12);
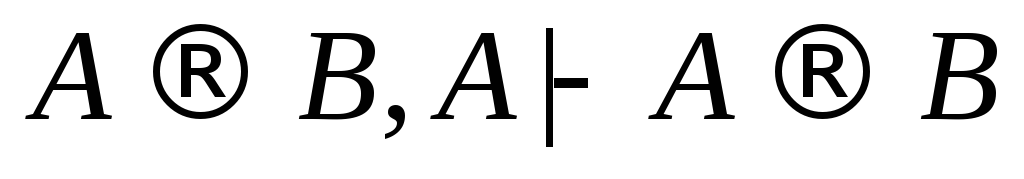
(4)		(из (2) по правилу 12);
(5)		(из (3) и (4) по правилу 8);
(6)		(из (5) по правилу 5);
(7)		(аксиома);
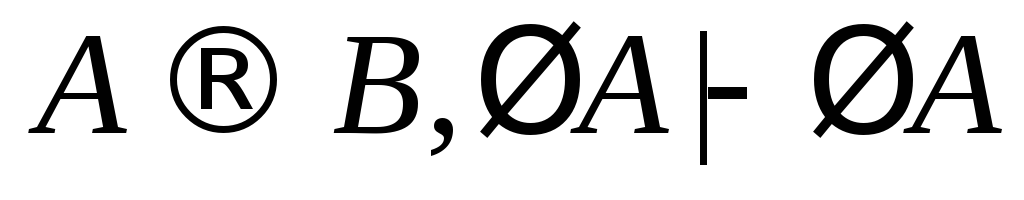
(8)		(из (7) по правилам 11, 12);
(9)		(из (8) по правилу 4);
(10)		(лемма 4);
(11)		(из (10) по правилу 12);
(12)		(из (6), (9), (11) по правилу 6).

Докажите самостоятельно следующие эквивалентности:

Используя только что перечисленные и ранее доказанные эквивалентности, мы можем упрощать выражения: заменять напереставлять слагаемые:переставлять сомножители:записывать выражения видабез скобок.

Введём общее обозначение для формул игде– атомарная формула. А именно, положимПусть– атомарные формулы. Выражение видабудем называтьэлементарной дизъюнкцией, если слагаемые в этом выражении все разные. При этом, вообще говоря, формулыне обязательно различные. В частности, элементарными дизъюнкциями являются выражения

Теорема 2. Для всякой формулырассматриваемой как выражение от атомарных формулсуществует формулатакая, чтои

где каждая скобка является элементарной дизъюнкцией.

Доказательство. Вначале избавимся в формулеот знака импликациииспользуя эквивалентностьДалее, пользуясь законами де-Морганаа также законом двойного отрицаниямы сможем добиться того, чтобы знаки отрицаниястояли только при атомарных формулах. Затем, используя дистрибутивностьмы сможем сделать так, чтобы внешним действием была конъюнкция, т.е. получить выражение видаНаконец, благодаря эквивалентностяммы можем привести подобные члены, после чего каждая скобка вдействительно будет элементарной дизъюнкцией.