Секвенции, правила вывода, доказательства

Секвенциямимы будем называть записи одного из следующих видов:

1. (2)

(3) (4)

Здесь – формулы ИВ, знакчитается “выводится”. Хотя в формальной теории мы не обязаны придавать смысл приводимым понятиям, в целях лучшего понимания формальных действий сделаем это. Секвенция (1) расшифровывается так: из формулвыводится формулаСеквенция (2) означает, что совокупность формулпротиворечива. Секвенция (3) означает, что формулавыводима. Секвенцию (4) мы комментировать не будем, она не имеет доказательства.

Аксиомами ИВ называются секвенции видагде– формула (не обязательно атомарная). Доказательства осуществляются на основеправил вывода, список которых мы приводим.

Правила вывода

(здесь – какие-либо последовательности формул, возможно, пустые):

1.		7.
2.		8.
3.		9.
4.		10.
5.		11.
6.		12.

Доказательством называется последовательность секвенций

где каждая – либо аксиома, либо получается из секвенцийс помощью правил вывода. Правило вывода применяется следующим образом: если секвенции, стоящие в числителе, уже встречались в доказательстве, то на любом дальнейшем шаге доказательства мы можем написать секвенцию, стоящую в знаменателе. Секвенцияназываетсядоказуемой(иливыводимой), еслиявляется членом какого-либо доказательства.

Пример. Докажем, чтоИмеем:

Здесь – аксиома;получена изприменением правила 12;– аксиома;получается изс помощью правила 12;– изс помощью правила 11 (считаем– изис помощью правила 1.

Лемма 2. Если секвенциядоказуема, то секвенциятакже доказуема.

Доказательство. Изпо правилу 7 получаем:Из аксиомыпо правилам 11, 12 (применённым, возможно, несколько раз) получаем:Затем изипо правилу 8 получаем:

Чтобы облегчить и ускорить поиск доказательств, сформулируем ещё несколько правил, каждое из которых строится на основе правил вывода 1 – 12. Будем называть их допустимыми правилами.

(а)
(б)
(в)		(з)
(г)		(и)
(д)		(к)
(е)		(л)
(ж)		(м)

Докажем некоторые из этих правил, оставляя доказательство других читателю в качестве упражнения.

(а) Доказательство этого правила получается применением правил 11 и 12.

(в)

Здесь (1) и (2) даны, (3) получается из (2) по правилу 7, а (4) из (1) и (3) по правилу 8.

Заметим, что из (в) следует

(надо лишь в секвенции дописать слева формулы из

(г) Докажем это правило в упрощённом виде: когда

(1)		(аксиома);
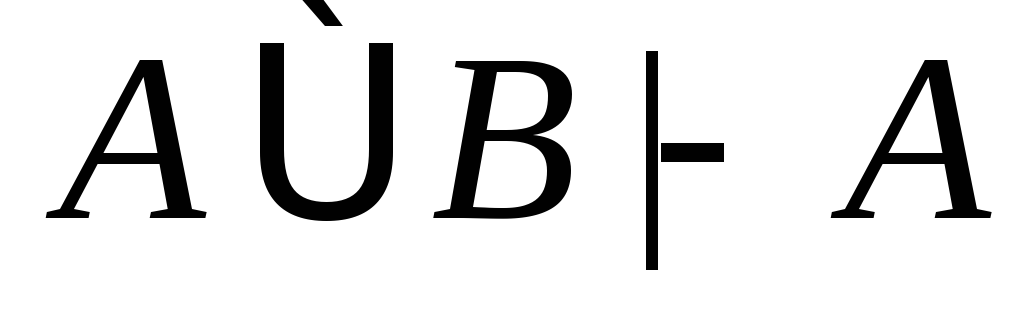
(2)		(из (1) по правилу 2);
(3)		(из (1) по правилу 3);
(4)		(из (3) по правилу 12);
(5)		(дано);
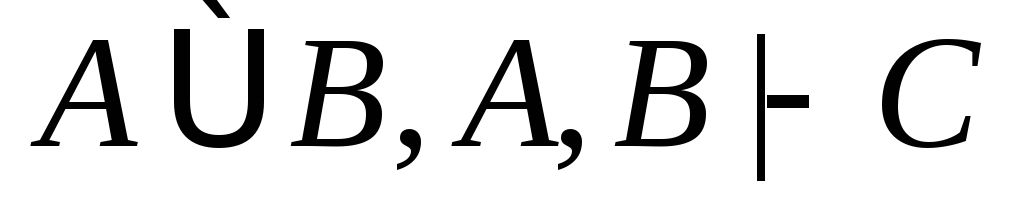
(6)		(из (5) по правилам (11),(12));
(7)		(из (4) и (6) по правилу (в));
(8)		(из (2) и (7) по правилу (в)).

(д)

(1)		(дано);
(2)		(из (1) по правилу 2);
(3)		(из (1) по правилу 3);
(4)		(из (2) и (3) по правилу 10).

(ж) Для доказательства этого правила докажем лемму.

Лемма 3.

Доказательство. С помощью аксиомипо правилам 11, 12 нетрудно получить, чтоиОтсюда по правилу 10 получаем:

Вернёмся к доказательству правила (ж). Нам надо доказать, что если секвенция имеет доказательство, тотакже имеет доказательство (оба доказательства должны основываться на правилах 1 – 12). Внимательный анализ правил вывода показывает, что получить секвенциюможно только по правилу 10. Значит, ранее были доказаны секвенцииидля некоторой формулыПропуская предыдущие шаги доказательства, будем иметь:

(1)
(2)
(3)		(из (1) по правилу 12);
(4)		(из (3) по правилу 11);
(5)		(из (4) по правилу (7));
(6)		(по лемме 3);
(7)		(из (6) по правилу 9);
(8)		(из (5) и (7) по правилу 8);
(9)-(13)	шаги, аналогичные шагам (3) - (7), где вместо (1) взято (2);
(14)		(аналогично (8));
(15)		(из (8) и (14) по правилу 10);
(16)		(из (15) по правилу 9).

(б) Докажем один частный случай правила (б), а именно,

(1)		(дано);
(2)		(из (1) по правилу (ж));
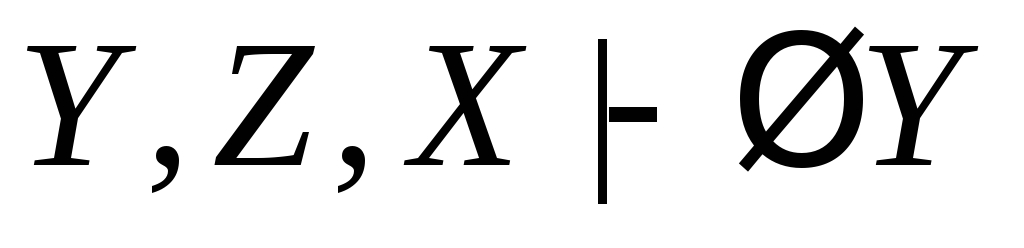
(3)		(из (2) по правилам 11, 12);
(4)		(аксиома);
(5)		(из (4) по правилу 12);
(6)		(из (3) и (5) по правилу 10).

Доказательства остальных правил предлагаются читателю в качестве самостоятельной работы.

Лемма 4. Для любой формулыдоказуема секвенция

Доказательство.

(1)		(аксиома);
(2)		(из (1) по правилу 5);
(3)		(аксиома);
(4)		(из (2) по правилу 12);
(5)		(из (3) по правилам 11, 12);
(6)		(из (4) и (5) по правилу 10);
(7)		(из (6) по правилам 9, 11);
(8)		(из (7) по правилу 4);
(9)		(из (3) и (8) по правилу 10);
(10)		(из (9) по правилу 9).

Лемма 5. Для любой формулыдоказуема секвенция

Доказательство.

(1)		(аксиома);
(2)		(из (1) по правилу 2);
(3)		(из (1) по правилу 3);
(4)		(из (2) и (3) по правилу 10).