1. Свойства множеств мощности континуума

1. с+с=с;

2. сс=с;

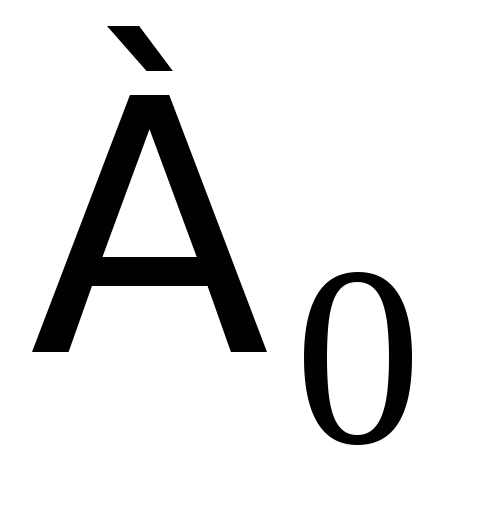3. с+=с=с.

Доказательство. Докажем вначале свойство 2), т.е. тот факт, что “квадрат содержит столько же точек, сколько отрезок”. Очевидно,с. Поэтому возьмёмНадо доказать, чтос. Ввиду теоремы Шрёдера – Бернштейна нам достаточно вложитьви вложитьвВложениевдля любого непустого множестваосуществляется очень просто:где– фиксированный элемент изТеперь вложим множествов множествоПустьТогдагдеЗапишемив виде бесконечных десятичных дробей:(как обычно, мы запрещаем дроби вида). Рассмотрим отображениеНетрудно проверить, что оно является вложением множествав

Свойство 1) можно доказать, используя 2) и теорему Шрёдера – Бернштейна. А именно, ясно, что множество мощности свкладывается в множество мощностис+с. Далее,с+с– это мощность объединения двух отрезков. Оно вкладывается в квадрат, а квадрат вкладывается в отрезок.

Свойство 3) доказывается аналогичными рассуждениями. Доказательство предоставляется читателю.

Пусть – произвольные множества. Обозначим черезмножество всех отображений

Теорема 3. Для любых множествимеет место эквивалентность

Доказательство. ПустьТогдаДля каждогопустьопределено правиломПо определениюЗначит, мы имеем отображениеЯсно, чтоПоложимМы получили отображение

Докажем, что Ф является вложением. Действительно, пусть Тогдапри некоторыхОтсюдаЗначит,а потомуТаким образом,т.е.– вложение.

Осталось доказать, что является наложением, т.е. что для каждогосуществует такоечтоИмеем:Значит,т.е.Таким образом,ПоложимТогдаОсталось проверить, чтоМы имеем:Ввиду произвольности элементаполучаем:По определениюЗначит,Ввиду произвольности элементаполучаем:Это и требовалось доказать.

Множество всех отображений множества в двухэлементное множествообозначим через

Теорема 4. Множествоэквивалентно множеству всех подмножеств множества

Доказательство. Каждому элементут.е. функциипоставим в соответствие– подмножество множестваИмеем отображениеНаоборот, каждому подмножествусоответствует функцияа именно,

Замечание. В дальнейшем мы будем отождествлять множествос множеством всех подмножеств множества

Связь между счётными множествами и множествами мощности континуума даёт следующая теорема.

Теорема 5.

Доказательство. Теорему можно переформулировать так: множество всех подмножеств счётного множества имеет мощность континуума. Ввиду теоремы Шрёдера – Бернштейна нам достаточно построить вложенияиКаждый элементможно задать последовательностью из 0 и 1; а именно,гдеВложениеимеет следующий вид:

Теперь вложим в. Элементы изпредставим в виде бесконечных двоичных дробей, запретив для однозначности записи видадля всех чисел, кромеВложениевосуществим так:гдесостоит из теху которых

Теорема 6 (Кантора). Для любого множества

Доказательство. Вложениеосуществляется просто:Нам осталось доказать, что не существует взаимно однозначного соответствия между множествамииПредположим, что существует взаимно однозначное соответствиет.е. каждому элементуставится в соответствие подмножествопричём каждое подмножествопредставимо в видепри некоторомПо условиюпри некоторомзначит,Далее,при некоторомв этом случаеПостроим подмножествомножестваполаживТак кактопри некоторомВыясним, верно ли соотношениеИмеем:

а) если топо определению множестваполучим:

б) если топо определению множестваполучим:что невозможно. Мы получили противоречие. Теорема доказана.

Из теоремы Кантора следует, что среди множеств нет наибольшего по мощности, так как, каково бы ни было множество множествоимеет ещё большую мощность. В частности,< ...