
3.2. Основные понятия теории моделей
Напомним
определения операций и отношений на
множестве. А именно, п-арной
операцией
на множестве
![]() называется отображение
называется отображение![]() При
При![]() мы получаем понятиебинарной
операции
мы получаем понятиебинарной
операции
![]() (например, сложение и умножение
действительных или натуральных чисел
являются бинарными операциями). При
(например, сложение и умножение
действительных или натуральных чисел
являются бинарными операциями). При![]() операция называетсяунарной.
Примерами унарных операций могут
служить: а) операция
операция называетсяунарной.
Примерами унарных операций могут
служить: а) операция
![]() взятия обратного элемента в группе, б)
операция
взятия обратного элемента в группе, б)
операция![]() транспонирования матриц, в) операция
транспонирования матриц, в) операция![]() умножения вектора на фиксированный
скаляр, г) комплексное сопряжение
умножения вектора на фиксированный
скаляр, г) комплексное сопряжение![]() При
При![]() мы получаемнуль-арную
операцию,
которая заключается в выделении в
множестве
мы получаемнуль-арную
операцию,
которая заключается в выделении в
множестве
![]() некоторого элемента.
некоторого элемента.
п-арным
отношением на
![]() называется отображение
называется отображение
![]() п-арное
отношение
иначе называют п-арным
(или п-местным)
предикатом.
Двуместный предикат
п-арное
отношение
иначе называют п-арным
(или п-местным)
предикатом.
Двуместный предикат
![]() – этобинарное
отношение
(к числу которых относятся =,
– этобинарное
отношение
(к числу которых относятся =,
![]()
![]()
![]() и т.д.). Одноместный предикат
и т.д.). Одноместный предикат![]() – этосвойство
элементов множества
– этосвойство
элементов множества
![]() (если
(если![]() мы говорим, что элемент
мы говорим, что элемент![]() обладает данным свойством, а при
обладает данным свойством, а при![]() – не обладает). Нульместный предикат –
это просто истина 1 или ложь 0 – он не
зависит от элементов множества
– не обладает). Нульместный предикат –
это просто истина 1 или ложь 0 – он не
зависит от элементов множества![]()
Вообще
говоря, понятие операции является в
некотором смысле излишним и может быть
выражено через понятие отношения.
Например, бинарная операция + на
множестве N
вполне определяется тернарным отношением
![]() В общем случаеп-арную
операцию
В общем случаеп-арную
операцию
![]() можно заменить
можно заменить![]() -арным
отношением
-арным
отношением![]() причём
причём![]() Однако, замену операции отношением
обычно не производят, так как операция
является привычным и удобным математическим
понятием.
Однако, замену операции отношением
обычно не производят, так как операция
является привычным и удобным математическим
понятием.
Определение.
Сигнатурой
называется пара
![]() где
где![]() – набор символов операций
– набор символов операций![]() – символ
– символ![]() -арной
операции),
-арной
операции),![]() – набор символов отношений
– набор символов отношений![]() – символ
– символ![]() -арного
отношения).
-арного
отношения).
Примеры
Группу можно рассматривать в сигнатуре
 (один символ операции умножения
(бинарной) и ни одного символа отношений)
или в сигнатуре
(один символ операции умножения
(бинарной) и ни одного символа отношений)
или в сигнатуре (один символ бинарной операции –
умножения и один символ унарной операции
– взятия обратного).
(один символ бинарной операции –
умножения и один символ унарной операции
– взятия обратного).Кольцо обычно рассматривают в сигнатуре
 иногда в сигнатуре
иногда в сигнатуре (0 – символ нульарной операции – взятия
нуля). Кольцо с единицей иногда
рассматривают в сигнатуре
(0 – символ нульарной операции – взятия
нуля). Кольцо с единицей иногда
рассматривают в сигнатуре иногда в сигнатуре
иногда в сигнатуре
 –обычная
сигнатура для упорядоченной группы
(здесь
–обычная
сигнатура для упорядоченной группы
(здесь


 –сигнатура
частично упорядоченного множества
(здесь Ф
–сигнатура
частично упорядоченного множества
(здесь Ф

В предыдущем разделе мы рассматривали множество натуральных чисел в сигнатуре
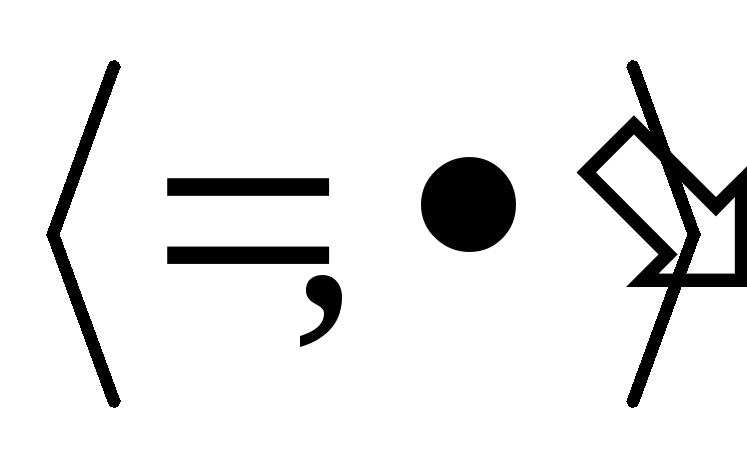 (штрих обозначает унарную операцию –
взятие следующего элемента).
(штрих обозначает унарную операцию –
взятие следующего элемента).
Замечание.
Следует различать п-арную
операцию от символа
п-арной
операции. Символ – это не сама операция,
а только значок
для неё. При этом, если сказано, что
![]() – символп-арной
операции, то нельзя вместо
– символп-арной
операции, то нельзя вместо
![]() подставлятьk-арную
операцию при
подставлятьk-арную
операцию при
![]() Такое же согласование должно быть между
символом отношения и самим отношением.
Такое же согласование должно быть между
символом отношения и самим отношением.
Определение.
Пусть
![]() – сигнатура.Моделью
сигнатуры
– сигнатура.Моделью
сигнатуры
![]() называется множество
называется множество![]() такое, что каждому символу операции
такое, что каждому символу операции![]() поставлена в соответствие операция той
же арности на множестве
поставлена в соответствие операция той
же арности на множестве![]() и каждому символу отношения
и каждому символу отношения![]() поставлено в соответствие отношение
поставлено в соответствие отношение![]() той же арности на множестве
той же арности на множестве![]() Операцию мы будем обозначать той же
буквой, что и символ операции, а отношение
– так же, как символ отношения. Множество
Операцию мы будем обозначать той же
буквой, что и символ операции, а отношение
– так же, как символ отношения. Множество![]() мы будем называтьносителем
модели.
мы будем называтьносителем
модели.
Приведём примеры.
Если задана сигнатура
 где
где – символ бинарной операции, то моделью
этой сигнатуры будет любое множество
– символ бинарной операции, то моделью
этой сигнатуры будет любое множество на котором задана одна бинарная операция.
Такое множество называетсягруппоидом.
Если эта операция ассоциативна (т.е.
на котором задана одна бинарная операция.
Такое множество называетсягруппоидом.
Если эта операция ассоциативна (т.е.
 то
то – полугруппа. Если
– полугруппа. Если удовлетворяет аксиомам группы
(ассоциативность, существование единицы,
существование обратного элемента), то
удовлетворяет аксиомам группы
(ассоциативность, существование единицы,
существование обратного элемента), то – группа.
– группа.Рассмотрим модель
 с двумя бинарными операциями. Среди
таких моделей выделяются кольца, поля,
тела и т.д. Интересно отметить, что эти
классы моделей так же, как в предыдущем
примере класс полугрупп и класс групп,
определяются каким-либо списком аксиом.
с двумя бинарными операциями. Среди
таких моделей выделяются кольца, поля,
тела и т.д. Интересно отметить, что эти
классы моделей так же, как в предыдущем
примере класс полугрупп и класс групп,
определяются каким-либо списком аксиом.Частично упорядоченное множество определяется как модель
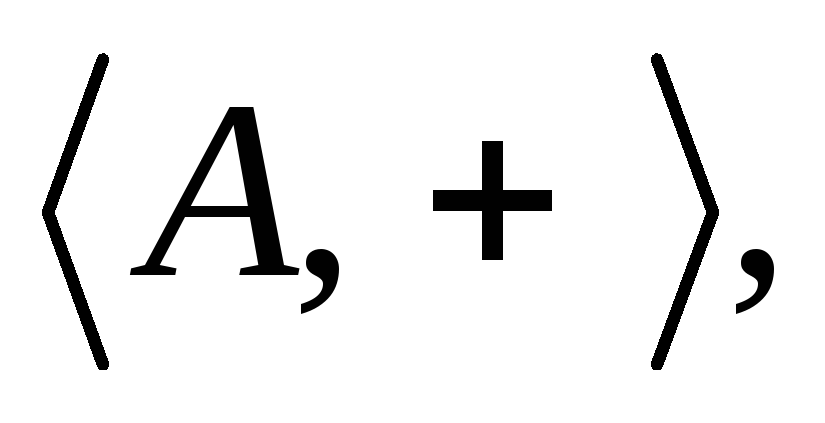 где
где – символ бинарного отношения,
удовлетворяющий следующим аксиомам:
1)
– символ бинарного отношения,
удовлетворяющий следующим аксиомам:
1) (рефлексивность), 2)
(рефлексивность), 2) (транзитивность), 3)
(транзитивность), 3) (антисимметричность). Если кроме этих
аксиом выполняется аксиома 4)
(антисимметричность). Если кроме этих
аксиом выполняется аксиома 4) (дихотомичность), то
(дихотомичность), то называется линейно упорядоченным
множеством, или цепью.
называется линейно упорядоченным
множеством, или цепью.
Термы и формулы логики первого порядка,
язык узкого исчисления предикатов
Пусть
задана сигнатура
![]() т.е. множество
т.е. множество![]() символов операций и множество
символов операций и множество![]() символов отношений.Язык
логики первого порядка
(другое название: язык
узкого исчисления предикатов (УИП)
содержит следующие символы:
символов отношений.Язык
логики первого порядка
(другое название: язык
узкого исчисления предикатов (УИП)
содержит следующие символы:
символы из множеств
 и
и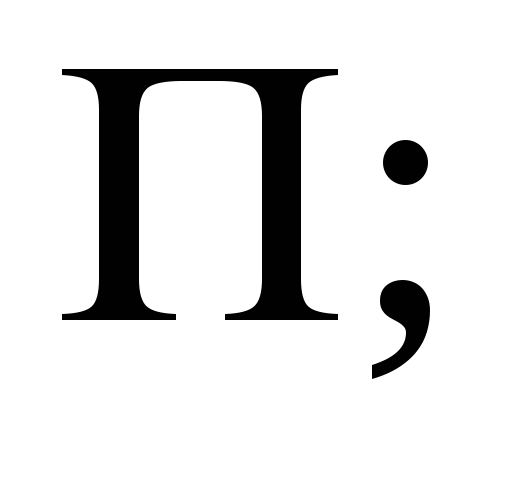
алфавит
 предметных
переменных;
их мы будем, как правило, обозначать
маленькими латинскими буквами
(преимущественно из второй половины
алфавита) с индексами или без, т.е.
предметных
переменных;
их мы будем, как правило, обозначать
маленькими латинскими буквами
(преимущественно из второй половины
алфавита) с индексами или без, т.е.
 алфавит
алфавит как правило, будет предполагаться
счётным;
как правило, будет предполагаться
счётным;логические связки:

служебные символы: “,”, “(”, “)” (запятая, левая и правая скобки).
Терм определяется индуктивно:
предметная переменная – терм;
если
 – термы и
– термы и – символп-арной
операции, то
– символп-арной
операции, то
 – терм.
– терм.
Приведём
примеры термов. Чтобы сделать обозначения
более привычными, мы будем несколько
отклоняться от предыдущего определения
и термы
![]()
![]() будем записывать в виде
будем записывать в виде![]()
![]()
Для сигнатуры
 следующие выражения являются термами:
следующие выражения являются термами:

 Последний терм мы будем писать в
сокращённом виде:
Последний терм мы будем писать в
сокращённом виде: а если имеет место ассоциативность
умножения, то можно записать
а если имеет место ассоциативность
умножения, то можно записать
В сигнатуре
 можно записать термы
можно записать термы

Если
 – символ тернарной операции, а
– символ тернарной операции, а – унарной, то
– унарной, то

 – термы.
– термы.
Формула
логики первого порядка и множество
свободных переменных
![]() формулы
формулы
![]() определяются индуктивно:
определяются индуктивно:
если
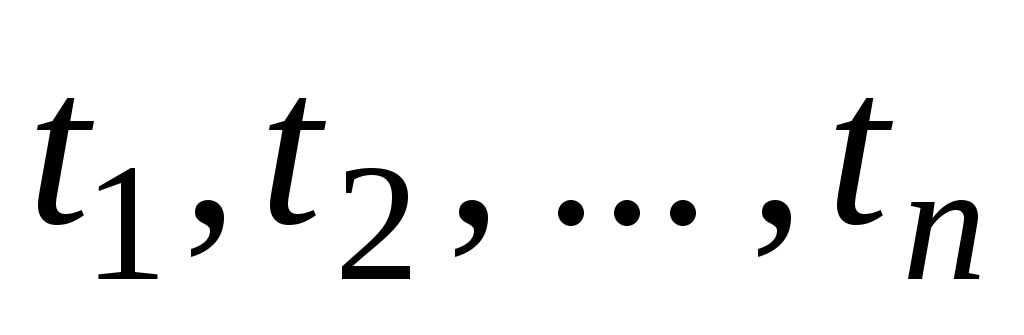 – термы и
– термы и – символп-местного
отношения, то
– символп-местного
отношения, то
 – формула (такие формулы называютсяатомарными);
свободными переменными формулы.
– формула (такие формулы называютсяатомарными);
свободными переменными формулы.
 называются предметные переменные,
входящие хотя бы в один из термов
называются предметные переменные,
входящие хотя бы в один из термов
если
 – формула, то
– формула, то – формула и
– формула и
если
 и
и – формулы и ни одна из предметных
переменных не входит свободно в одну
из этих формул, а несвободно в другую,
то
– формулы и ни одна из предметных
переменных не входит свободно в одну
из этих формул, а несвободно в другую,
то

 – формулы и
– формулы и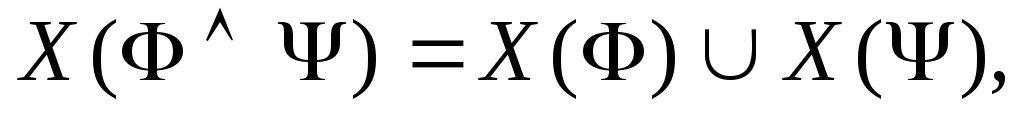


если
 – формула и
– формула и – предметная переменная, которая либо
не входит в формулу
– предметная переменная, которая либо
не входит в формулу либо входит в неё свободно, то
либо входит в неё свободно, то и
и – формулы и
– формулы и
Как
и в исчислении высказываний, для
облегчения восприятия формул мы часто
в выражениях вида
![]()
![]()
![]() внешние скобки будем опускать.
внешние скобки будем опускать.
Приведём примеры формул.
В сигнатуре
 формулами УИП являются следующие слова:
формулами УИП являются следующие слова:


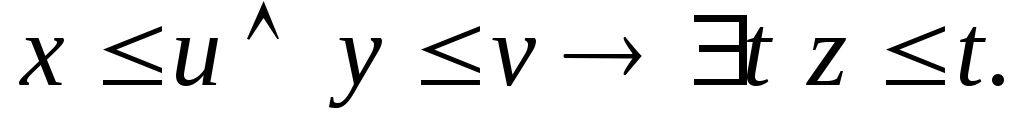
В сигнатуре
 где точка обозначает символ бинарной
операции, а = и
где точка обозначает символ бинарной
операции, а = и – соответственно символы бинарного и
тернарного отношений, примерами формул
являются::
– соответственно символы бинарного и
тернарного отношений, примерами формул
являются::

Формула
![]() называетсязамкнутой,
если она не содержит свободных переменных,
т.е.
называетсязамкнутой,
если она не содержит свободных переменных,
т.е.
![]() Замкнутую формулу можно назвать
высказыванием. Незамкнутые формулы
являются предикатами. Например,
Замкнутую формулу можно назвать
высказыванием. Незамкнутые формулы
являются предикатами. Например,![]() – замкнутая формула, а
– замкнутая формула, а![]() – незамкнутая, её можно рассматривать
как предикат от переменных
– незамкнутая, её можно рассматривать
как предикат от переменных![]() и
и![]()
![]()
![]() (здесь
(здесь![]() означает равенство по определению).
Легко видеть, чтовсякая
формула УИП является предикатом от
своих свободных переменных.
означает равенство по определению).
Легко видеть, чтовсякая
формула УИП является предикатом от
своих свободных переменных.
Пусть
![]() – модель, где
– модель, где![]() – носитель,
– носитель,![]() – сигнатура и
– сигнатура и![]() – формула УИП со свободными переменными
– формула УИП со свободными переменными![]() Истинность или ложность этой формулы
зависит от того, какие значения мы
придадим переменным
Истинность или ложность этой формулы
зависит от того, какие значения мы
придадим переменным![]() Назовёмоценкой
отображение
Назовёмоценкой
отображение
![]() (смысл её состоит в том, что мы каждой
предметной переменной присваиваем
какое-то значение из множества
(смысл её состоит в том, что мы каждой
предметной переменной присваиваем
какое-то значение из множества![]() Определимзначение
истинности
формулы
Определимзначение
истинности
формулы
![]() на оценке
на оценке
![]() Истину мы будем обозначать буквой И, а
ложь – буквой Л. Определение построим
индукцией по длине формулы. Положим
Истину мы будем обозначать буквой И, а
ложь – буквой Л. Определение построим
индукцией по длине формулы. Положим![]() ... ,
... ,![]()
Если

 – атомарная формула, где
– атомарная формула, где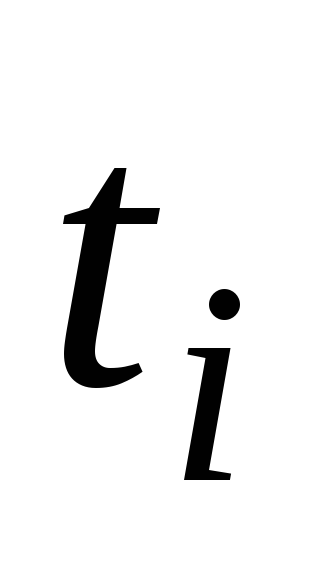 – термы, то
– термы, то в том и только том случае, если
в том и только том случае, если
если
 имеет вид
имеет вид

 или
или то истинность или ложность высказывания
то истинность или ложность высказывания определяется по обычным правилам;
определяется по обычным правилам;если

 то
то в том и только том случае, если
в том и только том случае, если при всех
при всех
если

 то
то в том и только том случае, если
в том и только том случае, если при каком-нибудь
при каком-нибудь
Выразимые и невыразимые предикаты.
