Статистика лб 2

Лабораторная работа 2

Метод наименьших квадратов. Аппроксимация рядов наблюдений. Регрессионный анализ.

2.1. Аппроксимация рядов наблюдений аналитической функцией.

Метод наименьших квадратов является одним из самых распространенных способов обработки результатов наблюдений. Будем описывать этот метод с помощью матричных форм.

Предположим, что в точках

получен ряд наблюдений

y_1,y_2,…..y_k.

Требуется найти коэффициенты   прямой линии

, (2.1)

исходя из системы уравнений

, (2.2)

(i=0,1,…k), называемых условной системой, и требования минимума средней квадратической ошибки

min (2.3)

Предполагается, что наблюдения искажены случайными ошибками, а значения x_i известны точно. Дифференцируя выражение (4.3) по  и  и приравнивая производные нулю, получим два линейных алгебраических уравнения для определения неизвестных::

(2.4)

(2.5)

Решая систему( 2.4)-(2.5), находим оценки параметров  и . Можно отметить, что матрица С системы (2.4)-(2.5) равна произведению двух прямоугольных матриц

=

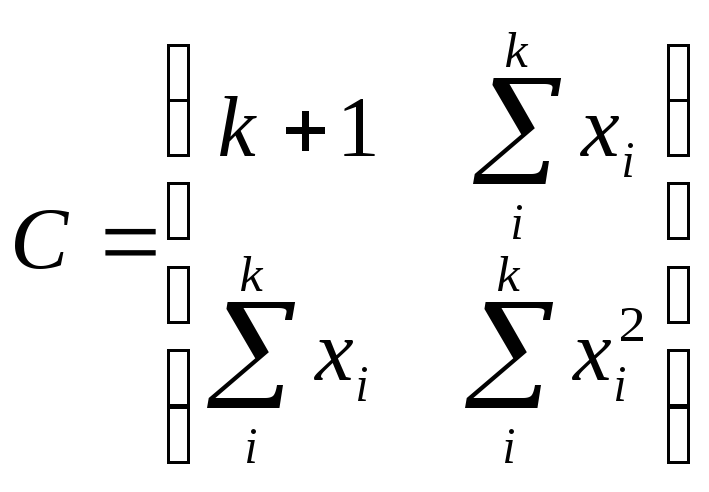
или

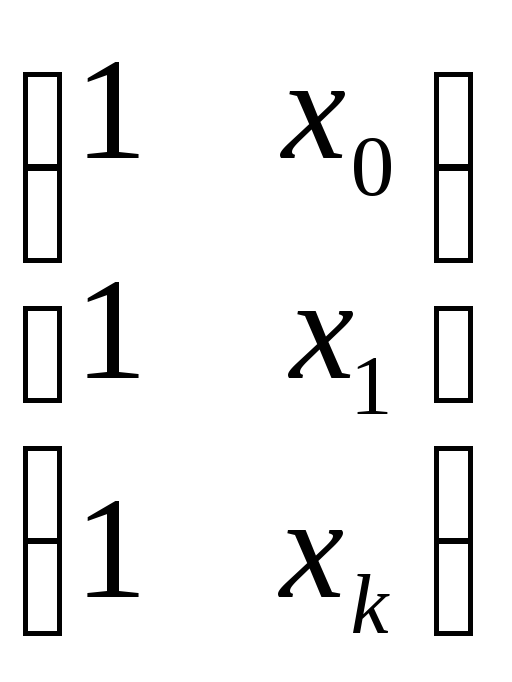
С=X^TX, где

X=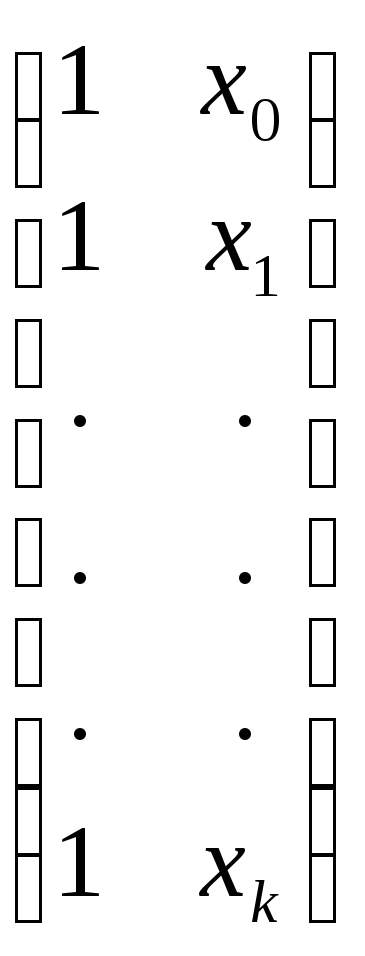- матрица системы (2.4) – (2.5) .

Наряду с линейной функцией ряды наблюдений можно аппроксимировать другими простыми аналитическими функциями, например, тригонометрическими функциями и экспонентами.

В качестве примера приведем аппроксимационную функцию вида

(2.6)

где

(2.7),

а T – период колебаний.

В случае m=2 ряд (4.6) имеет вид

(2.8)

Система нормальных уравнений в этом случае составляется из условия минимума функции

(2.9),

и имеет вид

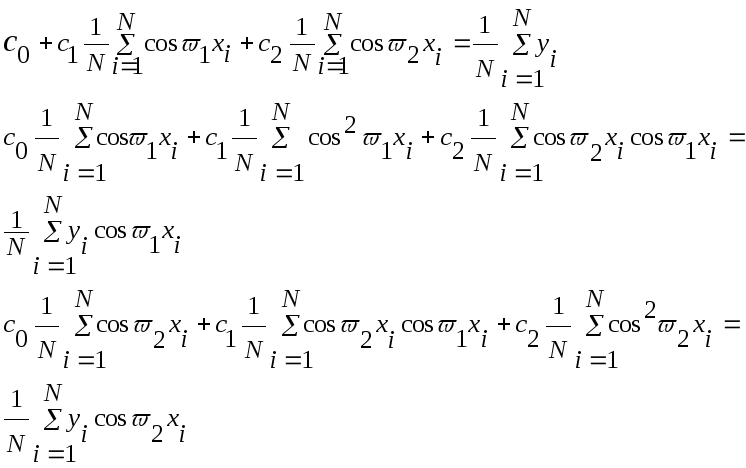(2.10)

Вычислив по значениям

все коэффициенты данной системы уравнений и решив ее, мы получим значения коэффициентов с₀, с₁ и с₂.

Примеры

По значениям функции при (),приведенным в таблице , методом наименьших квадратов произвести аппроксимацию функции следующей аналитической формулой

где а

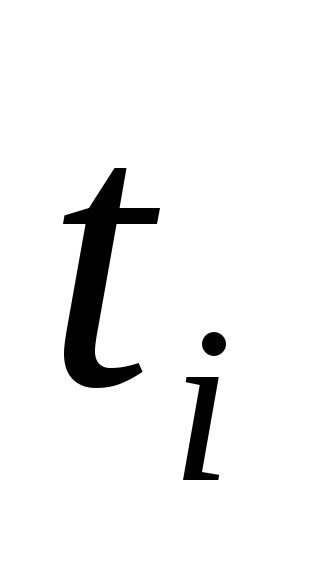сутки	0	0.5	1	1.5	2	2.5	3	3.5
yi	1.00	0.52	-0.40	-0.38	0	-0.38	-0.60	0.18
yi	1.00	0.53	-0.38	-0.39	0.01	-0.40	-0.59	0.19

2.2. Метод множественной линейной регрессии.

Рассмотрим теперь метод множественной линейной регрессии, который используется для целей физико-статистического прогноза.

Предположим, что между неизвестной величиной Y ( предсказуемое или предиктант) и известными переменными X_i (предсказатели или предикторы) существует линейная связь

(2.11),

где с_i - коэффициенты, которые находят методом наименьших квадратов по известным значениям Y и X_i для некоторой обучающей выборки из N случаев (k=1,2,…,N). При этом Nn.

Если ввести средние величины предикторов и предиктанта

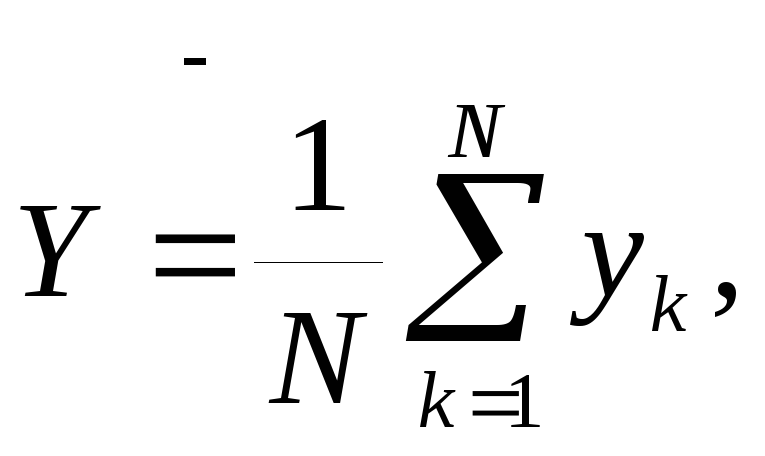
отклонения от них, то есть величины

,

то уравнение (4.6) можно записать в виде

В соответствии с методом наименьших квадратов для определения коэффициентов с_i имеем следующую систему нормальных уравнений

(2.12) где

,

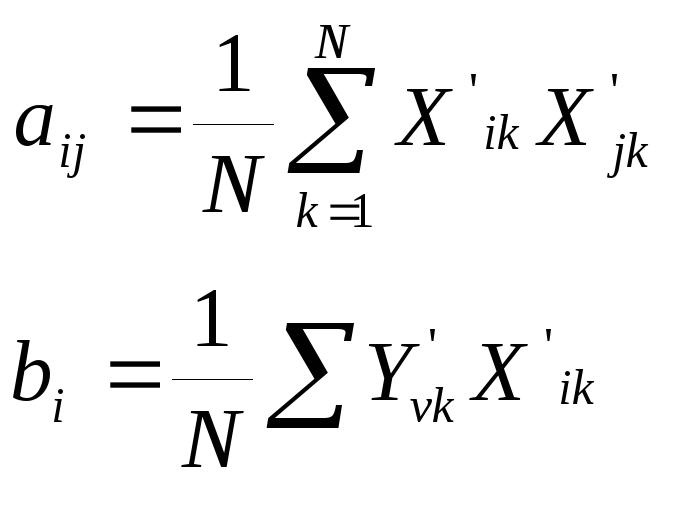Y’_vk – фактическое значение предиктанта по данным обучающей выборки.

В ходе решения системы нормальных уравнений ( или после решения и оценки коэффициентов) можно рассчитать ряд величин, характеризующих точность полученного уравнения регрессии ( точность, соответствующая данной обучающей выбрки). Средняя квадратическая (стандартная) погрешность вычисляется по формуле

(2.13)

относительная ошибка определяется по формуле

(2.14)

а сводный (множественный) коэффициент корреляции рассчитывается из соотношения

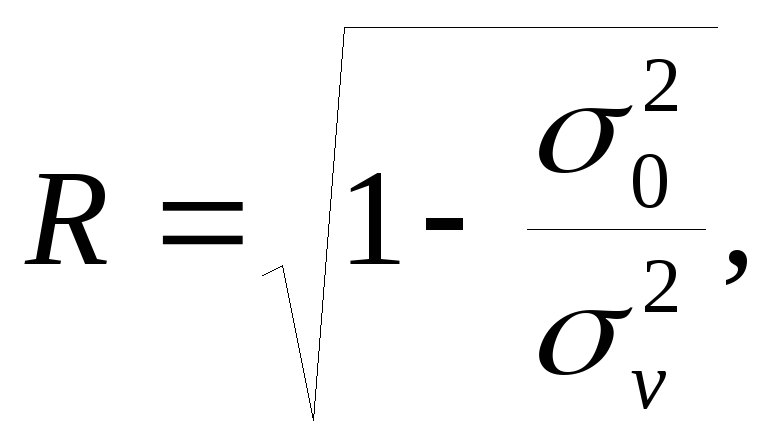(2.15),

где

(2.16)

средняя квадратическая величина Y_k^’.

Примеры.4.1.

Построить аппроксимационную кривую

по данным таблицы

x 1 2 3 4 5

y 671 970 1105 1285 1531

и построить данные таблицы и аппроксимационную функцию на графике

2.2.

Построить аппроксимационную кривую, вид которой представлен в примере 2.1. по данным таблиц

А

X 1 2 3 4 5 6 7 8

Y 150 300 550 680 900 1105 1280 1600

Б,

X 1 2 3 4 5 6 7 8

Y 0.1 0.22 0.33 0.45 0.6 0.65 0.7 0.79

В.

X 1 2 3 4 5 6 7 8

Y 65 75 81 92 101 111 120 132

и представить данные кривые на графике

ti	Xi	Cosω1ti	Cosω2ti	Cosω1ti *Cosω2ti	(Cosω1ti)2	(Cosω2ti)2	x Cosω1ti	x Cosω2ti	X апр
0	1	1	1	1	1	1	1	1	1
0.5	0.52	0.7	0	0	.49	0	.364	0	.36
1.0	-0.40	0	-1	0	0	1	0	.4	-.5
1.5	-.38	-0.7	0	0	.49	0	.267	0	-.35
2.0	0	-1	1	-1	1	1	0	0	0.01
2.5	-0.38	-0.7	0	0	.49	0	.267	0	.35
3.0	-0.6	0	-1	0	0	1	0	.6	-.5
3.5	0.18	-.7	0	0	.49	0	.126	0	.35
сумма	-0.06	0	0	0	3.96	4	2.024	2.0

С₀=0.0

С₁=0.51

С₂=0.5

ti	1	2	3	4	5	6 7
x	1	3	5	8	10	11 12
ti2	1	4	9	16	25	36 49
xiti	1	6	15	32	50	66 84